A body is thrown with a velocity equal to n times the escape velocity (ve). Velocity of the body at large distance away will be :-
ve√n2−1
ve√n2+1
ve√1−n2
None of these
The correct Answer is:A
To solve the problem, we need to find the velocity of a body thrown with a velocity equal to n times the escape velocity (ve) at a large distance from the Earth.
1. Understand Escape Velocity:
The escape velocity ve from the surface of the Earth is given by the formula:
ve=√2GMR
where G is the gravitational constant, M is the mass of the Earth, and R is the radius of the Earth.
2. Initial Velocity:
The body is thrown with an initial velocity v0=nve.
3. Mechanical Energy Conservation:
The total mechanical energy (kinetic + potential) is conserved. At the surface of the Earth, the total mechanical energy Ei is:
Ei=Kinetic Energy+Potential Energy
The initial kinetic energy KEi is:
KEi=12m(nve)2=12mn2v2e
The initial potential energy PEi at the surface of the Earth is:
PEi=−GMmR
Therefore, the total initial energy is:
Ei=12mn2v2e−GMmR
4. Final Energy at Large Distance:
At a large distance, the potential energy PEf is zero, and the total energy Ef is just the kinetic energy:
Ef=KEf=12mv2
5. Setting Initial Energy Equal to Final Energy:
Since mechanical energy is conserved, we have:
Ei=Ef
Substituting the expressions for Ei and Ef:
12mn2v2e−GMmR=12mv2
6. Simplifying the Equation:
We can cancel m from both sides (assuming m≠0):
12n2v2e−GMR=12v2
7. Substituting ve:
Substitute ve=√2GMR:
12n2(2GMR)−GMR=12v2
Simplifying gives:
n2GMR−GMR=12v2
(n2−1)GMR=12v2
8. Solving for v2:
Multiply both sides by 2:
2(n2−1)GMR=v2
9. Taking the Square Root:
Finally, taking the square root gives:
v=√2(n2−1)GMR
10. Substituting Back for ve:
Since 2GMR=v2e:
v=ve√n2−1
Final Answer:
The velocity of the body at a large distance away will be:
v=ve√n2−1
The escape velocity ve from the surface of the Earth is given by the formula:
ve=√2GMR
where G is the gravitational constant, M is the mass of the Earth, and R is the radius of the Earth.
The body is thrown with an initial velocity v0=nve.
The total mechanical energy (kinetic + potential) is conserved. At the surface of the Earth, the total mechanical energy Ei is:
Ei=Kinetic Energy+Potential Energy
The initial kinetic energy KEi is:
KEi=12m(nve)2=12mn2v2e
The initial potential energy PEi at the surface of the Earth is:
PEi=−GMmR
Therefore, the total initial energy is:
Ei=12mn2v2e−GMmR
At a large distance, the potential energy PEf is zero, and the total energy Ef is just the kinetic energy:
Ef=KEf=12mv2
Since mechanical energy is conserved, we have:
Ei=Ef
Substituting the expressions for Ei and Ef:
12mn2v2e−GMmR=12mv2
We can cancel m from both sides (assuming m≠0):
12n2v2e−GMR=12v2
Substitute ve=√2GMR:
12n2(2GMR)−GMR=12v2
Simplifying gives:
n2GMR−GMR=12v2
(n2−1)GMR=12v2
Multiply both sides by 2:
2(n2−1)GMR=v2
Finally, taking the square root gives:
v=√2(n2−1)GMR
Since 2GMR=v2e:
v=ve√n2−1
The velocity of the body at a large distance away will be:
v=ve√n2−1
Topper's Solved these Questions
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - B (OBJECTIVE TYPE QUESTIONS)
22 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - C (PREVIOUS YEARS QUESTIONS)
51 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - EXERCISE
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
9 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
Similar Questions
If a body is projected with a speed lesser than escape velocity, then
View SolutionA body is projected horizontally from the surface of the earth (radius =R) with a velocity equal to n times the escape velocity. Neglect rotational effect of the earth. The maximum height attained by the body from the earth s surface is R/2. Then, n must be
View SolutionA body is projected up with a velocity equal to 3/4th of the escape velocity from the surface of the earth. The height it reaches is (Radius of the earth is R)
View SolutionWhat is the maximum height attained by a body projected with a velocity equal to one- third of the escape velocity from the surface of the earth? (Radius of the earth=R)
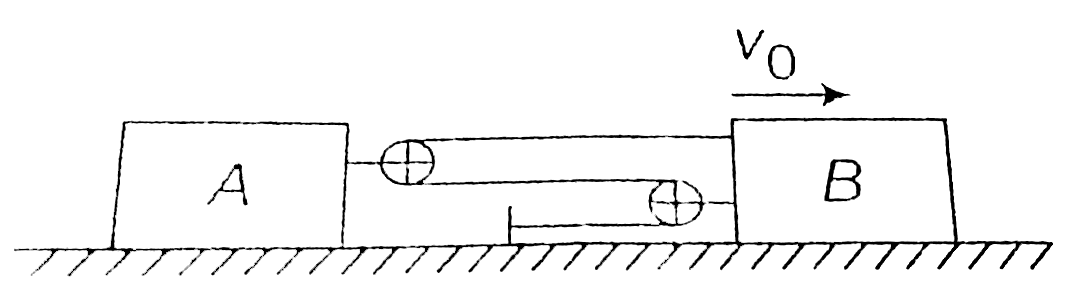
View SolutionBlock B moves to the right with a constant velocity v0. The velocity of body a relative to b is
View SolutionA body is projected vertically upwards from the surface of a planet of radius R with a velocity equal to half the escape velocity for that planet. The maximum height attained by the body is
View SolutionA body is projected vertically upwards from the surface of a planet of radius R with a velocity equal to half the escape velocity for that planet. The maximum height attained by the body is
View SolutionAn objects is projected vertically upwards from the surface of the earth with a velocity 3 times the escape velocity ve from earth's surface. What will be its final velocity after escape from the earth's gravitational pull ?
View SolutionA body is projected vertically upwards from the surface of a planet of radius R with a velocity equal to 1/3rd the escape velocity for the planet. The maximum height attained by the body is
View SolutionA body attains a height equal to the radius of the earth. The velocity of the body with which it was projected is
View Solution