A pipe of varying area of cross-section is held such that its axis is horizontal. At two cross sections A and B, its radii are 8 cm and 4 cm. If velocity of water at A through the pipe is 16 cm s−1 and pressure at A is 106 dyne/cm2 , find the pressure at cross-section B.
To find the pressure at cross-section B of a pipe with varying cross-section, we can apply the principles of fluid dynamics, specifically the continuity equation and Bernoulli's theorem. Here’s a step-by-step solution:
Step 1: Determine the Areas of Cross Sections A and B
Given the radii:
- Radius at A, rA=8cm
- Radius at B, rB=4cm
The area of a circle is given by the formula:
A=πr2
Calculating the areas:
- Area at A:
AA=π(8cm)2=64πcm2
- Area at B:
AB=π(4cm)2=16πcm2
Step 2: Use the Continuity Equation
The continuity equation states that the product of the cross-sectional area and the velocity of the fluid must be constant along the flow:
AA⋅VA=AB⋅VB
Where:
- VA=16cm/s (velocity at A)
- VB is the unknown velocity at B.
Rearranging the equation to solve for VB:
VB=AA⋅VAAB
Substituting the values:
VB=(64π)⋅(16)16π=64⋅1616=64cm/s
Step 3: Apply Bernoulli's Theorem
Bernoulli's theorem states:
PA+12ρV2A+ρghA=PB+12ρV2B+ρghB
Since the pipe is horizontal, the heights hA and hB are equal, thus the gravitational potential energy terms cancel out. We can simplify to:
PA+12ρV2A=PB+12ρV2B
Rearranging gives us:
PB=PA+12ρV2A−12ρV2B
Step 4: Substitute Known Values
Given:
- PA=106dyne/cm2
- VA=16cm/s
- VB=64cm/s
- Density of water ρ=1g/cm3=1000kg/m3=1000dyne/cm3
Substituting into the equation:
PB=106+12(1000)(16)2−12(1000)(64)2
Calculating the kinetic energy terms:
=106+8000−2048000
=106−2040000+8000
=106−2040000+8000=998080dyne/cm2
Final Answer
Thus, the pressure at cross-section B is:
PB=998080dyne/cm2≈99.808×104dyne/cm2
Given the radii:
- Radius at A, rA=8cm
- Radius at B, rB=4cm
A=πr2
Calculating the areas:
- Area at A:
AA=π(8cm)2=64πcm2
- Area at B:
AB=π(4cm)2=16πcm2
The continuity equation states that the product of the cross-sectional area and the velocity of the fluid must be constant along the flow:
AA⋅VA=AB⋅VB
Where:
- VA=16cm/s (velocity at A)
- VB is the unknown velocity at B.
VB=AA⋅VAAB
Substituting the values:
VB=(64π)⋅(16)16π=64⋅1616=64cm/s
Bernoulli's theorem states:
PA+12ρV2A+ρghA=PB+12ρV2B+ρghB
Since the pipe is horizontal, the heights hA and hB are equal, thus the gravitational potential energy terms cancel out. We can simplify to:
PA+12ρV2A=PB+12ρV2B
Rearranging gives us:
PB=PA+12ρV2A−12ρV2B
Given:
- PA=106dyne/cm2
- VA=16cm/s
- VB=64cm/s
- Density of water ρ=1g/cm3=1000kg/m3=1000dyne/cm3
PB=106+12(1000)(16)2−12(1000)(64)2
Calculating the kinetic energy terms:
=106+8000−2048000
=106−2040000+8000
=106−2040000+8000=998080dyne/cm2
Thus, the pressure at cross-section B is:
PB=998080dyne/cm2≈99.808×104dyne/cm2
Similar Questions
Water flows through a horizontal pipe of varying area of cross-section at the rate 5 cubic metre per minute. What is the velocity of water at a point where pipe radius is 10 cm?
View SolutionWater flows through a horizontal pipe of varying area of cross-section at the rate 5 cubic metre per minute. What is the velocity of water at a point where pipe radius is 10 cm?
View SolutionA horizontal pipe of varying cross-sectional area carries water flowing at a constant rate. The pressure at sections (1) and (2) are 50cm and 20cm of Hg. If the velocity of section (1) is 5m/s, what is the velocity of section (2). Also determine the ratio of areas at sections (1) and (2) (as shown in Fig.
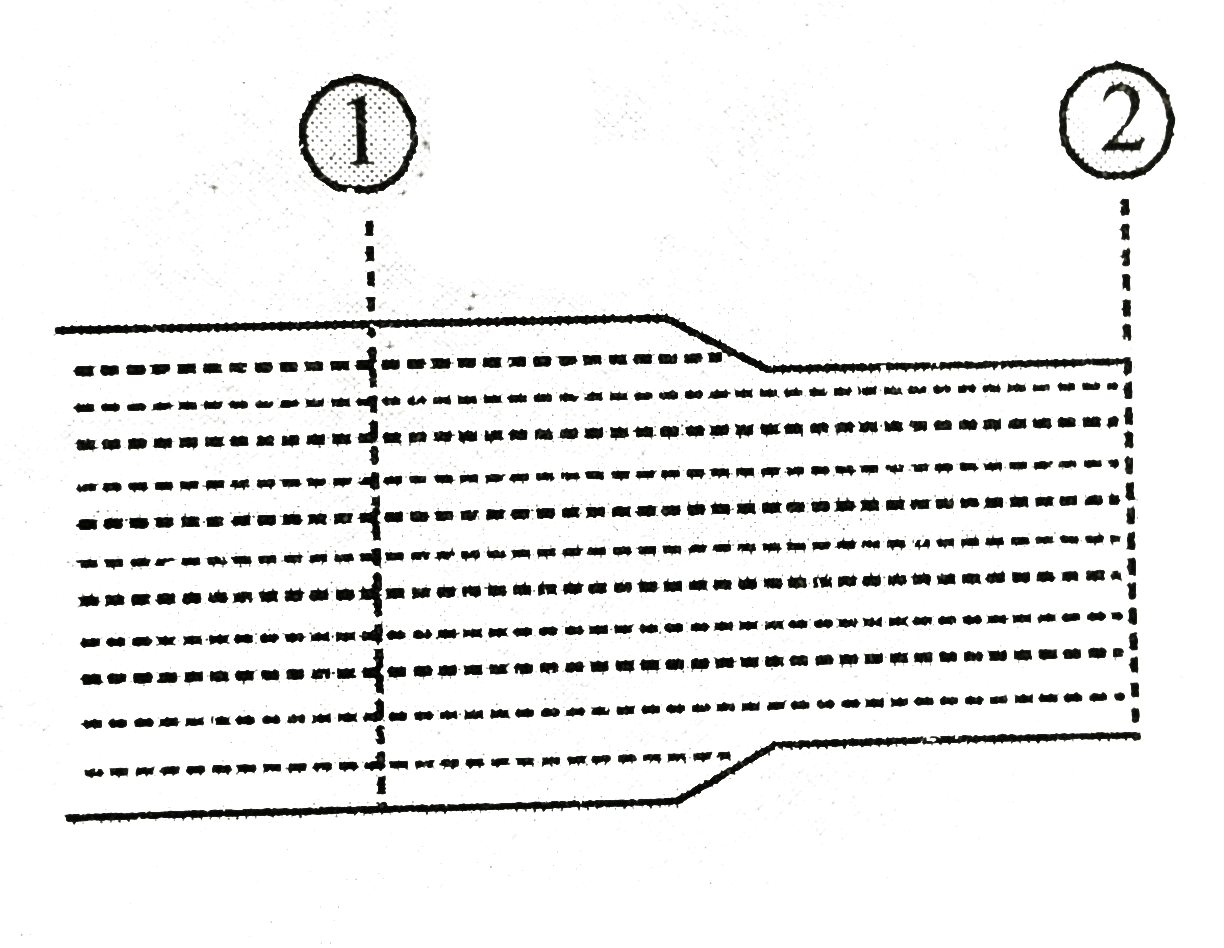 View Solution
View SolutionA horizontal pipe of area of cross-section a and 3a respectively, then the ratio of velocity of flow at two different cross-section (If flow is streamline) is
View SolutionA pipe of constant cross - section is bent in a horizontal plane as shown in the figure . Points A and B are located on two different streamlines . Then
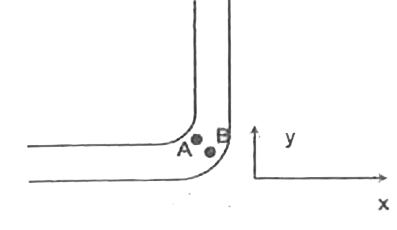 View Solution
View SolutionThe cross-sectionss of a pipe at two points A and B are in the ratio 1.4. If the speed of water flowing through the pipe at point A is v, its speed at point B is
View SolutionWater flows along horizontal pipe whose cross-section is not constant. The pressure is 1 cm of Hg, where the velocity is 35 cm/s . At a point where the velocity is 65cm/s then pressure will be
View SolutionA lawn sprinkler has 20 holes, each of cross-sectional area 2.0x10−2cm2, and is connected to a hose pipe of cross sectional area 2.4cm2. If the speed of water in the hose pipe is 1.5ms−1, the speed of water as it emerges from the holes is
View SolutionWater flows along horizontal pipe whose cross-section is not constant. The pressureis 1 cam of Hg, where the veloecity is 35 cm/s . At a point where the velocity is 65cm/s then pressure will be
View SolutionA pipe of non uniform cross section has two distinct section 1 and 2 with areas 2cm2 and 4cm2 respectively. If the velocity of flowing liquid at section 1 is 5cm/s, determine the velocity at section 2.
View Solution

