A flat plate of area is placed on a flat surface and is separated from it by a film of oil m thick whose coefficielnt of .viscosity is . The force required to cause the plate to slide on the surface at constant speed of is
10 N
15 N
20 N
25 N
To find the force required to slide a flat plate on a flat surface at a constant speed, we can use the formula for viscous force. The viscous force Fv can be calculated using the equation:
Fv=η⋅A⋅dvdy
where:
- η is the coefficient of viscosity,
- A is the area of the plate,
- dv is the relative speed of the plate,
- dy is the thickness of the oil film.
Step 1: Identify the given values
From the problem statement, we have:
- Area of the plate, A=0.1m2
- Thickness of the oil film, dy=10−5m
- Coefficient of viscosity, η=1.5N⋅s/m2
- Speed of the plate, v=1mm/s=1×10−3m/s
Step 2: Substitute the values into the formula
We need to calculate the rate of change of velocity with respect to the distance, which is dvdy. Since the speed is constant, we can directly substitute the values into the formula:
Fv=η⋅A⋅vdy
Substituting the values:
Fv=1.5N⋅s/m2⋅0.1m2⋅1×10−3m/s10−5m
Step 3: Calculate dvdy
Calculating dvdy:
dvdy=1×10−310−5=100
Step 4: Substitute dvdy back into the formula
Now substituting dvdy back into the equation for Fv:
Fv=1.5⋅0.1⋅100
Step 5: Calculate the viscous force
Calculating Fv:
Fv=1.5⋅0.1⋅100=15N
Conclusion
The force required to cause the plate to slide on the surface at a constant speed of 1mm/s is 15N.
- η is the coefficient of viscosity,
- A is the area of the plate,
- dv is the relative speed of the plate,
- dy is the thickness of the oil film.
From the problem statement, we have:
- Area of the plate, A=0.1m2
- Thickness of the oil film, dy=10−5m
- Coefficient of viscosity, η=1.5N⋅s/m2
- Speed of the plate, v=1mm/s=1×10−3m/s
We need to calculate the rate of change of velocity with respect to the distance, which is dvdy. Since the speed is constant, we can directly substitute the values into the formula:
Calculating dvdy:
Now substituting dvdy back into the equation for Fv:
Calculating Fv:
The force required to cause the plate to slide on the surface at a constant speed of 1mm/s is 15N.
Similar Questions
A metal plate 5cm×5 cm rests on a layer of castor oil 1 mm thick whose coefficient of viscosity is 1.55Nsm−2 . Find the horizontal foce required to move the plate with a speed of 2 cm/s
View SolutionA plate of area 100cm2 is placed on the upper surface of castor oil, 2mm thick. Taking the coefficient of viscosity to be 15.5 poise, calculate the horizontal force necessary to move the plate with a velocity 3cms−1.
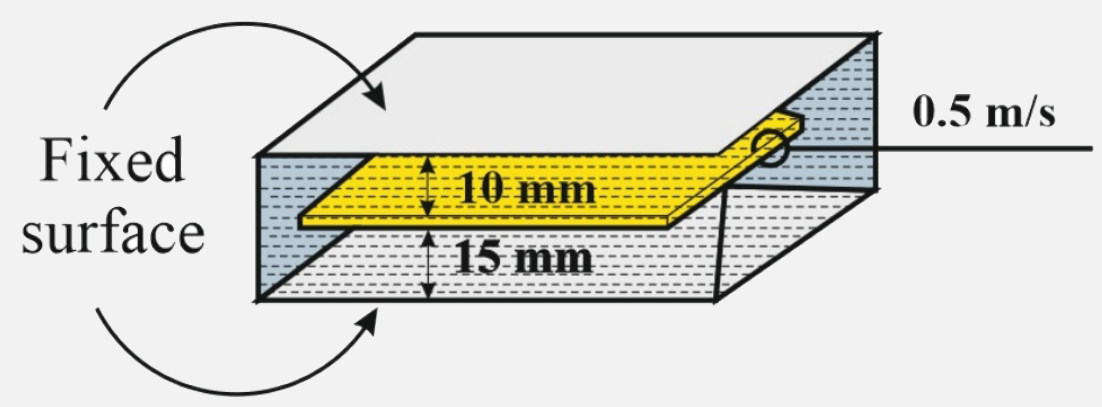
View SolutionGlycerine is filled in 25 mm wide space between two large plane horizontal surfaces. A thin plate of area 0.75m2 at a distance of 10 mm from one of the surfaces is in a horizontal position be the plates inside the glycerine. It is dragged horizontally at a constant speed of 0.5ms2. Take coefficient of viscosity η= 0.5 Ns m−2. What is the force required to drag the plate at a constant speed (in newton) ?
View Solutionflat plate is separated from a large plate by a layer of glycerine of thickness 3×10−3m. If the coefficient of viscosity of glycerine is2Ns/m2 what is the force required to keep the plate moving with a velocity of6×10−2m/s. Area of the plate is 4.8×10−3m
View SolutionBetween a plate of area 100cm2 and another plate of area 100m2 there is a 1mm, thick layer of water, if the coefficient of viscosity of water is 0.01 poise, then the force required to move the smaller plate with a velocity 10cms−1 with reference to large plate is
View SolutionAflat plate of area 0.05m2 is separated from another large plate at rost by a liquid layer of uniform thickness 1μm. The tangential force needed to move the smaller plate with a constant velocity of 10cms−1 i s 20 N. Calculate the coefficent of viscosity of the liquid.
View SolutionA metal plate 0.04m2 in area is lying on a liquid layer of thickness 10−3m and coefficient of viscosity 140 poise. Calculate the horizontal force needed to move the plate with a speed of 0.040 m/s.
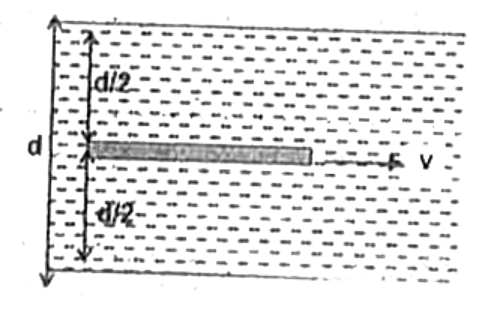
View SolutionA thin square plate of side φ=10cm is dragged with constant velocity v=3 cm/s in an oil . The width 'd' of the oil column is 2mm. Square plate is placed symmetrically as shown in the figure. Assumed velocity of layer of oil at the end is negligible. The coefficient of viscosity is 150 poise. Find the horizontal force (in Newton) required to move the square plate with constant velocity
View SolutionThere is a 1mm thick layer of glycerine between a flat plate of area 100cm2 and and a big plate. If te coefficient of viscosity of glycerine is 1.0kg/m−sec, then how much force is required to move the plate with a velocity of 7 cm/sec.
View SolutionThe space between two large horizontal metal plates, 6cm apart, is filled with a liquid of viscosity 0.8N/m2 . A thin plate of surface area 0.01m2 is moved parallel to the length of the plate such that the plate is at a distance of 2m from one of the plates and 4cm from the other. If the plate moves with a constant speed of 1ms−1, then
View Solution
