The neck and bottom of a bottle are 3 cm and 15 cm in radius respectively. If the cork is pressed with a force 12 N in the neck of the bottle, then force exerted on the bottom of the bottle is :-
30N
150N
300N
600N
To solve the problem, we will use the concept of pressure and the relationship between force, area, and pressure.
1. Identify the Given Values:
- Radius of the neck of the bottle, r1=3cm=0.03m
- Radius of the bottom of the bottle, r2=15cm=0.15m
- Force applied at the neck, F1=12N
2. Calculate the Areas:
- The area of the neck of the bottle, A1:
A1=πr21=π(0.03)2=π×0.0009≈0.002827m2
- The area of the bottom of the bottle, A2:
A2=πr22=π(0.15)2=π×0.0225≈0.070685m2
3. Apply the Pressure Equation:
- According to Pascal's principle, the pressure in the neck of the bottle is equal to the pressure at the bottom of the bottle:
P1=P2
- This can be expressed in terms of force and area:
F1A1=F2A2
4. Rearranging to Find F2:
- Rearranging the equation gives:
F2=F1×A2A1
5. Substituting the Values:
- Substitute F1, A1, and A2:
F2=12N×A2A1=12N×π(0.15)2π(0.03)2=12N×(0.15)2(0.03)2
- Simplifying further:
F2=12N×0.02250.0009=12N×25=300N
6. Final Result:
- The force exerted on the bottom of the bottle is F2=300N.
Answer:
The force exerted on the bottom of the bottle is 300 N.
- Radius of the neck of the bottle, r1=3cm=0.03m
- Radius of the bottom of the bottle, r2=15cm=0.15m
- Force applied at the neck, F1=12N
- The area of the neck of the bottle, A1:
A1=πr21=π(0.03)2=π×0.0009≈0.002827m2
- The area of the bottom of the bottle, A2:
A2=πr22=π(0.15)2=π×0.0225≈0.070685m2
- According to Pascal's principle, the pressure in the neck of the bottle is equal to the pressure at the bottom of the bottle:
P1=P2
- This can be expressed in terms of force and area:
F1A1=F2A2
- Rearranging the equation gives:
F2=F1×A2A1
- Substitute F1, A1, and A2:
F2=12N×A2A1=12N×π(0.15)2π(0.03)2=12N×(0.15)2(0.03)2
- Simplifying further:
F2=12N×0.02250.0009=12N×25=300N
- The force exerted on the bottom of the bottle is F2=300N.
The force exerted on the bottom of the bottle is 300 N.
Similar Questions
(a) The diameter of neck and bottom of a bottle are 2 cm and 10 cm respectively. The bottle is completely filled with oil. If the cork in the neck is pressed in with a force of 1.2kgf , what force is exerted on the bottom of the bottle ?
(b) Name the law/ principle you have used to find the force in part (a)
View SolutionA bucket has top and bottom diameters of 40 cm and 20 cm respectively. Find the volume of the bucket if its depth is 12 cm. Also, find the cost of tin sheet used for making the bucket at the rate of Rs 1.20 per cm2 .
View Solution
Knowledge Check
Two syringes of different cross-section (without needle filled with water are connected with a tightly fitted rubber tube filled with water. Diameters of the smaller piston an larger piston are 1cm and 3cm respectively. If a force of 10N is applied to the smaller piston then the force exerted on the larger piston is
A30NB60 NC90 ND100 N
The area of cross section of the two arms of a hydraulilc press are 1 cm^2 and 10 cm^2 respectively figure. A force of 5N is applied on the water in the thinner arm. What force should be applied on the water in the thicker arm so that the water may remain in equilibrium?
 ,
,
View SolutionThe area of cross section of the two arms of a hydraulilc press are 1 cm^2 and 10 cm^2 respectively figure. A force of 5N is applied on the water in the thinner arm. What force should be applied on the water in the thicker arm so that the water may remain in equilibrium?
 ,
,
View SolutionA bottle has an opening of radius a and length b. A cork of length b and radius (a+ΔA) is compressed to fit into the opening completely (See figure). If the bulk modulus of cork is B and frictional coefficient between the bottle and cork is ? then the force needed to push the cork into the bottle is :
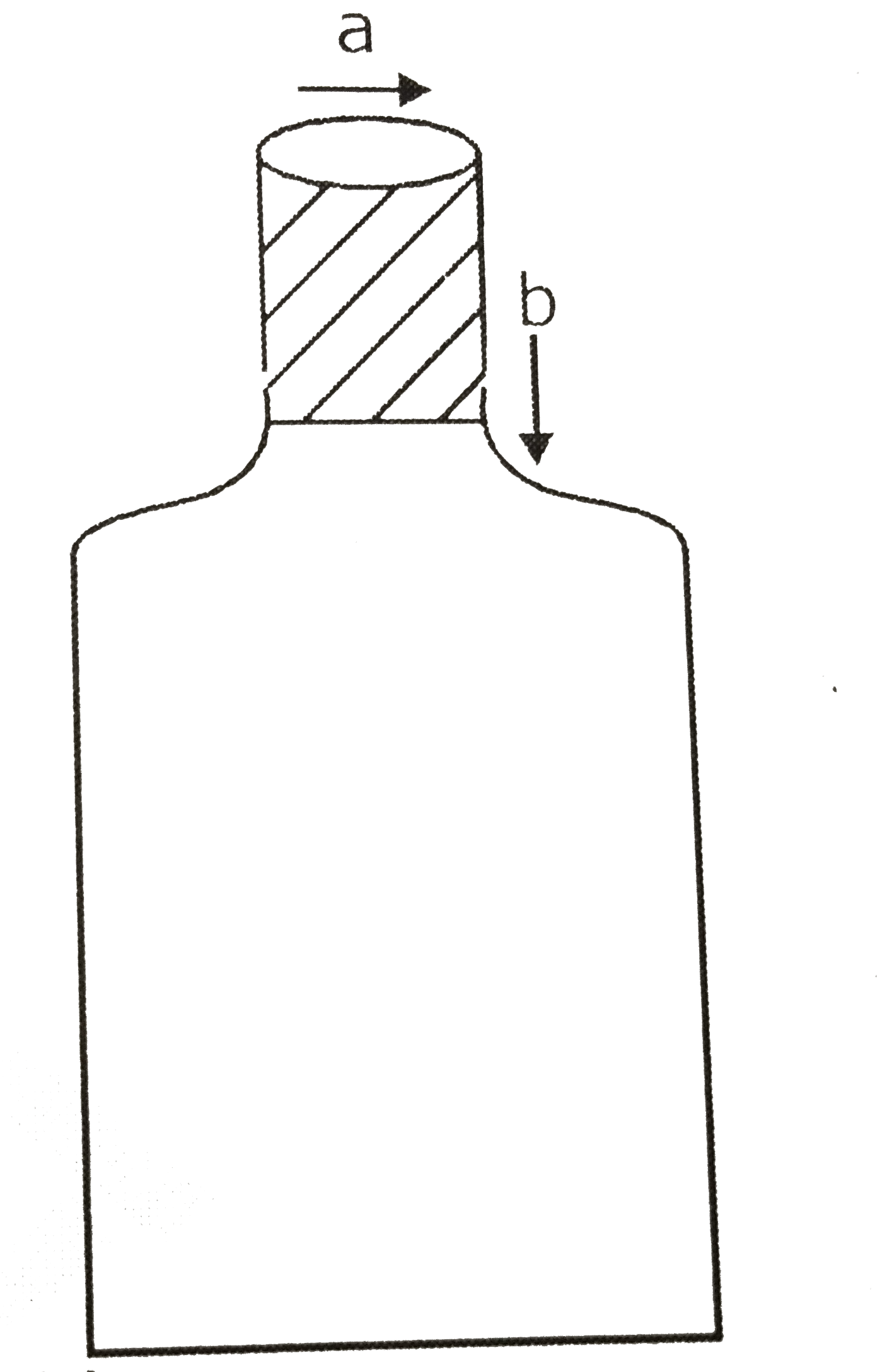
View SolutionThe area of cross sectioin of the two arms of a hydraulic press is 1cm2 and 20cm2 respectively. A force of 10N is applied on the water in the thinner arm. What force should be applid on the water in the thicker arms so that water may remain in equilibrium?

View SolutionA glass full of water upto a height of 10 cm has a bottom of are 10cm2, top of area 30cm2 and volume 1 litre.
(a) Find the force exerted by the water on the bottom.
(b) Find the resultant force exerted by the sides of the glass on the water.
(c ) If the glass is convered by a jar and the air inside the jar is completely pumped out, what will be the answer to parts (a) and (b).
(d) If a glass of different shape is used, provided the height, the bottom area, the top area and the volume are unchanged, will the answer to parts (a) and (b) change.
Take g=10m/s3, density of water=103kg/m3 and atmospheric pressure =1.01×105N/m2.
View SolutionA bucket is in form of a frustum of a cone with a capacity of 12308.8cm3of water. The radii of the top and bottom circular ends are 20 cm and 12 cm respectively. Find the height of the bucket and the area of the metal sheet used in its making. [ Use π=3.14.]
View SolutionA curved glass vessel full of water upto a height of 10 cm has a bottom of area 10cm2, top of area 30cm2 and volume 1 L.
(i) Find the force exerted by the water on the bottom.
(ii) Find the resultant force exerted by the sides of the glass on the water.
(iii) If the glass vessel is covered by a jar and the air inside the jar is completely pumped out, what will be the answers to parts (a) and (b)
(iv) If a glass vessel of different shape is used provided the height, the bottom area and the volume are unchanged, will the answers to parts (a) and (b) change.
(Take, g=10ms−2 , density of water =103kgm−2 and atmospheric pressure =1.01×105Nm−2)
View Solution
