A liquid X of density 3.36g/cm3 poured in a U-tube which contains Hg. Another liquid Y is poured in left arm with heght 8 cm upper levels of X and Y are same. What is density of Y?
0.8gcc^(-1)
1.2gcc^(-1)
1.4gcc^(-1)
1.6gcc^(-1)
To solve the problem, we need to analyze the pressure balance in the U-tube containing the two liquids and mercury. Here's a step-by-step solution:
Step 1: Understand the Setup
We have a U-tube with:
- Liquid X of density ρX=3.36g/cm3 on the right arm.
- Liquid Y poured into the left arm with a height of hY=8cm.
- Mercury in the U-tube, which has a density ρHg=13.6g/cm3.
The upper levels of liquids X and Y are the same.
Step 2: Apply Pascal's Law
According to Pascal's law, the pressure at the same horizontal level in a fluid is the same. Therefore, we can equate the pressures at the level where the two liquids meet.
Let PA be the pressure at the level of liquid Y and PB be the pressure at the level of liquid X.
Step 3: Write the Pressure Equations
The pressure at point A (in the left arm) can be expressed as:
PA=ρY⋅g⋅hY+ρHg⋅g⋅hHg
Where hHg is the height of mercury column above the level of liquid Y.
The pressure at point B (in the right arm) can be expressed as:
PB=ρX⋅g⋅hX
Where hX is the height of liquid X above the same level.
Step 4: Set the Pressures Equal
Since PA=PB:
ρY⋅g⋅8+ρHg⋅g⋅2=ρX⋅g⋅10
Step 5: Cancel Out Common Terms
We can cancel g from both sides:
ρY⋅8+ρHg⋅2=ρX⋅10
Step 6: Substitute Known Values
Substituting ρX=3.36g/cm3 and ρHg=13.6g/cm3:
ρY⋅8+13.6⋅2=3.36⋅10
ρY⋅8+27.2=33.6
Step 7: Solve for ρY
Rearranging the equation gives:
ρY⋅8=33.6−27.2
ρY⋅8=6.4
ρY=6.48=0.8g/cm3
Final Answer
The density of liquid Y is ρY=0.8g/cm3.
---
We have a U-tube with:
- Liquid X of density ρX=3.36g/cm3 on the right arm.
- Liquid Y poured into the left arm with a height of hY=8cm.
- Mercury in the U-tube, which has a density ρHg=13.6g/cm3.
According to Pascal's law, the pressure at the same horizontal level in a fluid is the same. Therefore, we can equate the pressures at the level where the two liquids meet.
The pressure at point A (in the left arm) can be expressed as:
PA=ρY⋅g⋅hY+ρHg⋅g⋅hHg
Where hHg is the height of mercury column above the level of liquid Y.
PB=ρX⋅g⋅hX
Where hX is the height of liquid X above the same level.
Since PA=PB:
ρY⋅g⋅8+ρHg⋅g⋅2=ρX⋅g⋅10
We can cancel g from both sides:
ρY⋅8+ρHg⋅2=ρX⋅10
Substituting ρX=3.36g/cm3 and ρHg=13.6g/cm3:
ρY⋅8+13.6⋅2=3.36⋅10
ρY⋅8+27.2=33.6
Rearranging the equation gives:
ρY⋅8=33.6−27.2
ρY⋅8=6.4
ρY=6.48=0.8g/cm3
The density of liquid Y is ρY=0.8g/cm3.
Similar Questions
A vertical U shaped tube of uniform cross-section contains mercury in both limbs. Another liquid of density 3.4gcm3 is poured In one limb of column length 4 cm as shown in figure. Then difference (h) between the upper level of liquid in both the limbs is (densityofmercury=13.6gcm3)
View SolutionThere are three different liquids ( liquid 1 , liquid 2 and liquid 3) having density 13.6 gm/cc ., 1.3 gm/cc and 0.8 gm/cc . Liquid 1 is poured separately into the two arms till upper surface of liquid 2 & 3 are same . What is the height of liquid 3 if height of liquid 2 is 16 cm ?
View SolutionLength of horizontal arm of a uniform cross section U-tube is l=21cm and ends of both of the vertical arms are open to surrounding of pressure 10500N/m2. A liquid of density ρ=103kg/m3 is poured into the tube such that liquid just fills the horizontal part of the tube. Now one of the open ends is sealed and the tube is then rotated about a vertical axis passing through the other vertical arm With angular velocity ω0=10rad/s. If length of each vertical arm is a=6cm, calculate the length of air column in the sealed arm. (in cm)

View SolutionA manometer contains a liquid of density 5.44g/cm3 is attached to a flask containing gas 'A' as follows
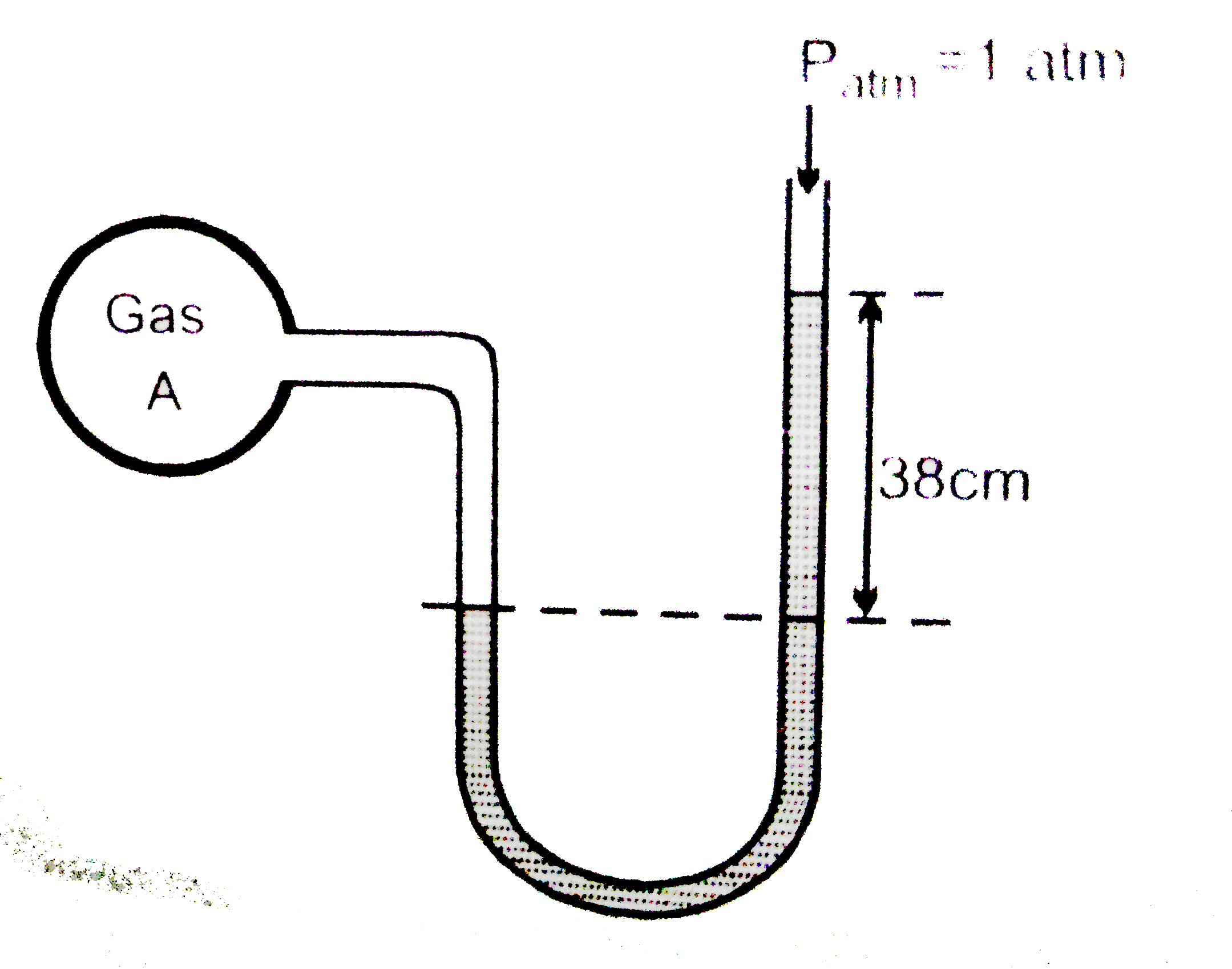
If the same liquid is used in barometer to measure the atmospheric pressure, then what will be the lengh of the liquid columnm which exerts pressure equal to 1 atm ? (density of Hg=13.6g/cm3)
View SolutionA monometer contains a liquid of density 5.44g/cm3 is attached to a flask containing gas A'asfollows<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/NRA_PHY_CHM_JMA_C03_E01_213_Q01.pngwh=80%sty≤=background:white;><br>Ifthesameliqusused∈¯ometer→measuretheatmosphericpressure,thenwˆwillbethe≤n>hoftheliquolumn,whichexertspressureequal→1atm?(densityofHg=13.6g//cm^(3))
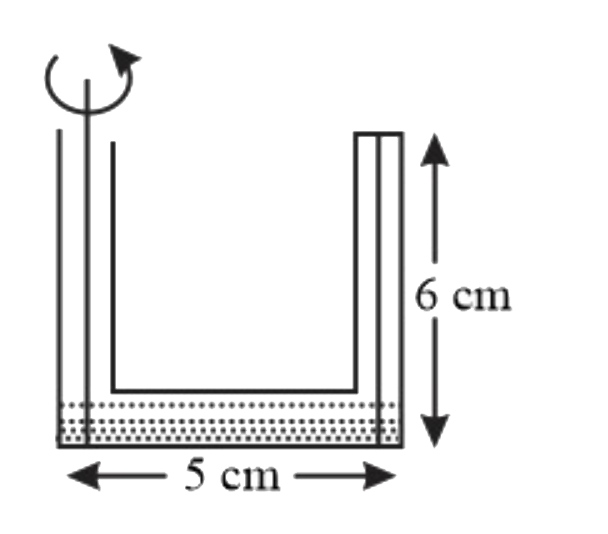
View SolutionLength of the horizontal arm of a uniform cross - section U - tube is l = 5 cm and both ends of the vertical arms are open to the surrounding pressure of 7700 N m−2. A liquid of density ρ=103 kg m−3 is poured into the tube such that the liquid just fills the horizontal part of the tube. Now, one of the open ends is sealed and the tube. Now, one of the open ends is sealed and the tube is then rotaed about a vertical axis passing through the other veritcal arm with angular velocity ω due to which the liquid rises up to half the length of the vertical arm. If length of each vertical arm is a = 6 cm. What is the value of ω(in rad s−1)?
View SolutionA manometer tube contains a liquid of density 4×103kgm−3. When connected to a vessel containing a gas, the liquid level in the other arm of the tube is higher by 20 cm. When connected to another sample of enclosed gas, the liquid level in the other arm of the manometer tube falls 8 cm below the liquid level in the first arm. Which of the two samples exerts more pressure and by what amount ?
View Solution_S01_015_Q01.png)
A vertical U-tube of uniform cross-section contains mercury in both arms A glycerine (relative density =1.3) column of length 10 cm is introduced into one of the arms. Oil of density 800 gm m−3 is poured into the other arm until the upper surface of the oil and hlycerine are at the same horizontal level, find the length of the column. Density of mercury is 13.6×103kgm−3
View SolutionA tube U-shaped has a uniform cross-sectionn with arm length l1andl2(l1>l2). Tube has a liquid of density ρ1 filled to a height h. another liquid of density ρ2=(ρ1)14 is poured in arm A. both liquids are immiscible. the length of second liquid that should be poured in A so that first overtone of A is in unisom with fundamental tone of B is:

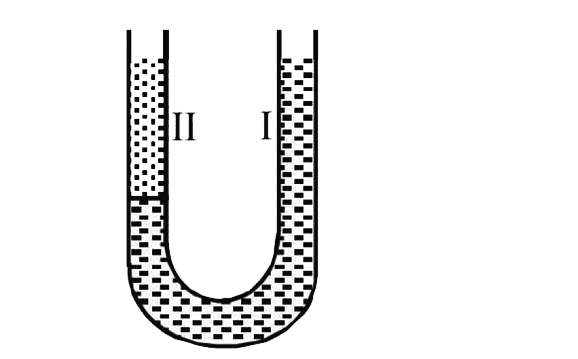
View SolutionA U-tube of uniform cross section (see figure) is partially filled with a liquid I. Another liquid II which does not mix with liquid I is poured into one side. It is found that the liquid levels of the two sides of the tube are the same, while the level of liquid I has risen by 2cm. If the specific gravity of liquid I is 1.1, the specific gravity of liquid II must be
View Solution
