There are two charges +2μC and −3μC. The ratio of forces acting on them will be
(1) 2:3 (2) 1:1
(3) 3:2 (4) 4:9
To solve the problem of finding the ratio of forces acting on two charges, we can follow these steps:
1. Identify the Charges: We have two charges, q1=+2μC and q2=−3μC.
2. Understand the Forces: According to Coulomb's Law, the forces between two point charges are equal in magnitude and opposite in direction. Thus, the force exerted by charge q1 on charge q2 (denoted as F12) is equal in magnitude to the force exerted by charge q2 on charge q1 (denoted as F21).
3. Apply Coulomb's Law: The formula for the force between two charges is given by:
F=14πϵ0|q1⋅q2|r2
where r is the distance between the charges and ϵ0 is the permittivity of free space.
4. Calculate the Forces:
- For F12 (force on q2 due to q1):
F12=14πϵ0|(+2μC)⋅(−3μC)|r2
- For F21 (force on q1 due to q2):
F21=14πϵ0|(−3μC)⋅(+2μC)|r2
5. Observe the Magnitudes: Since both forces are calculated using the same formula and the product of the charges remains the same, we have:
F12=F21
6. Find the Ratio of Forces:
F12F21=1
This means the ratio of the forces acting on the charges is 1:1.
Conclusion:
The ratio of forces acting on the two charges is 1:1. Therefore, the correct answer is option (2) 1:1.
---
F=14πϵ0|q1⋅q2|r2
where r is the distance between the charges and ϵ0 is the permittivity of free space.
- For F12 (force on q2 due to q1):
F12=14πϵ0|(+2μC)⋅(−3μC)|r2
- For F21 (force on q1 due to q2):
F21=14πϵ0|(−3μC)⋅(+2μC)|r2
F12=F21
F12F21=1
This means the ratio of the forces acting on the charges is 1:1.
The ratio of forces acting on the two charges is 1:1. Therefore, the correct answer is option (2) 1:1.
Similar Questions
There are two charges +1μC and−5μC under mutual coulombic interaction . The ratio of magnitude of forces acting on themwill be
View SolutionThere are two charge +1μc and +2μc kept at certain separation ,the ratio of electrostatic forces acting on them will be in the ratio
View SolutionThe radii of two circles are in the ratio 2: 3. The ratio of their areas is
(a) 2:3
(b) 4:9
(c) 3:2
(d) 9:4
View SolutionIf the ratio of the areas of two square is 9:1, then the ratio of their perimeters is (a) 2:1 (b) 3:1 (c) 3:2 (d) 4:1
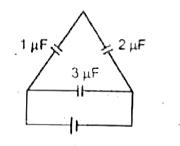
View SolutionIn given circuit, ratio of charge on 2 μF capacitor to the charge of 3 μ F capacitor will be
View SolutionIf the heights of two cones are in the ratio of 1:4 and the radii of their bases are in the ratio 4:1, then the ratio of their volumes is (a) 1:2 (b) 2:3 (c) 3:4 (d) 4:1
View SolutionThe product of the coefficients of terms in −43ab2+14bc2+3ca2 is
(a)1 (b) 12 (c)−1 (d) 3
View SolutionIf the angles of a triangle are in the ratio 4:1:1, then the ratio of the longest side to the perimeter is (a)√3:(2+√3) (b) 1:6 (c)1:2+√3 (d) 2:3
View SolutionA right angled prism of refractive index μ1 is placed in a rectangular block of refractive index μ2 , which is surrounded by a medium of refractive index μ3 ,as shown in the figure . A ray of light 'e' enters the rectangular block at normal incidence . depending upon the relationship between μ1,μ2andμ3 , it takes one of the four possible paths 'ef' , 'eg' , 'eh' or 'ef'
_E01_228_Q01.png)
Match the paths in List I with conditions of refractive indices in List II and select the correct answer using the codes given below the lists:
{:("List" I , "List" II) , ( P. e rarr f , 1. mu_(1)gt sqrt(2mu_(2))) , ( Q. e rarr g , 2. mu_(2) gt mu_(1) "and" mu_(2) gt mu_(3)), ( R. e rarr f , 3. mu_(1) = mu_(2)), ( S. e rarr f , 4. mu_(2) lt mu_(1) lt sqrt(2mu_(2)) "and" mu_(2) gt mu_(3)):}<br>Codes:<br>{:( P , Q , R , S) , ((A) 2 , 3 , 1 , 4), ((B) 1 , 2 , 4 , 3) , ((C) 4 , 1 , 2 , 3) , ((D) 2, 3 , 4 , 1):}
View SolutionThe force experienced by a charge of 2μC in an electric field is 3×10−3N. The intensity of the electric field.
View Solution
