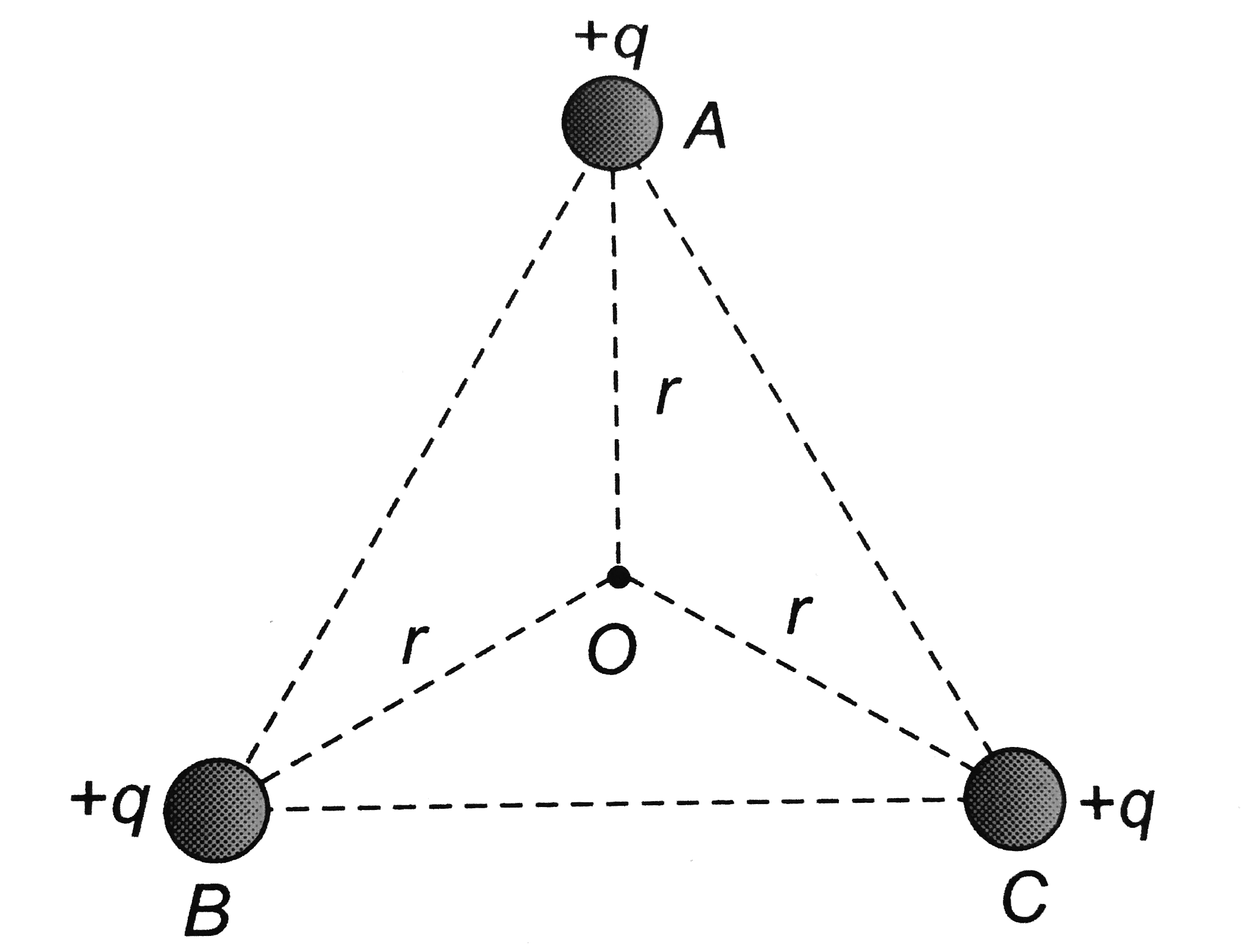
ABC is an equilateral triangle. Charges +q are placed at each corner. The electric field intensity at the centroid of triangle will be
14πε0×qr2
14πε0×3qr2
14πε0×qr
Zero
The correct Answer is:D
To find the electric field intensity at the centroid of an equilateral triangle with charges +q placed at each corner, follow these steps:
1. Identify the Setup:
- Consider an equilateral triangle ABC with side length a.
- Charges +q are placed at each corner A, B, and C.
- We need to find the electric field intensity at the centroid O of the triangle.
2. Electric Field Due to a Single Charge:
- The electric field due to a single charge +q at a distance r is given by:
E=14πϵ0qr2
- In an equilateral triangle, the distance from each vertex to the centroid O is:
r=a√3
3. Calculate the Electric Field Magnitude:
- The electric field due to charge +q at one vertex (say A) at the centroid O is:
EA=14πϵ0q(a√3)2=14πϵ0q⋅3a2=3q4πϵ0a2
4. Direction of Electric Fields:
- The electric field vectors due to charges at A, B, and C will point away from each charge because they are positive charges.
- The angle between any two electric field vectors at the centroid is 120∘.
5. Resultant Electric Field Calculation:
- Let EA, EB, and EC be the electric fields due to charges at A, B, and C respectively.
- Since EA=EB=EC in magnitude, we can use vector addition to find the resultant electric field.
- The resultant electric field ER at the centroid O due to two charges (say A and B) is given by:
EAB=√E2A+E2B+2EAEBcos(120∘)
- Since cos(120∘)=−12:
EAB=√E2A+E2A+2EAEA(−12)=√E2A+E2A−E2A=EA
- Similarly, the resultant of EAB and EC will also be zero because they are equal in magnitude and symmetrically opposite.
6. Conclusion:
- The electric fields due to the three charges at the centroid O cancel each other out.
- Therefore, the net electric field intensity at the centroid O is:
EO=0
Final Answer:
The electric field intensity at the centroid of the triangle is 0.
- Consider an equilateral triangle ABC with side length a.
- Charges +q are placed at each corner A, B, and C.
- We need to find the electric field intensity at the centroid O of the triangle.
- The electric field due to a single charge +q at a distance r is given by:
E=14πϵ0qr2
- In an equilateral triangle, the distance from each vertex to the centroid O is:
r=a√3
- The electric field due to charge +q at one vertex (say A) at the centroid O is:
EA=14πϵ0q(a√3)2=14πϵ0q⋅3a2=3q4πϵ0a2
- The electric field vectors due to charges at A, B, and C will point away from each charge because they are positive charges.
- The angle between any two electric field vectors at the centroid is 120∘.
- Let EA, EB, and EC be the electric fields due to charges at A, B, and C respectively.
- Since EA=EB=EC in magnitude, we can use vector addition to find the resultant electric field.
- The resultant electric field ER at the centroid O due to two charges (say A and B) is given by:
EAB=√E2A+E2B+2EAEBcos(120∘)
- Since cos(120∘)=−12:
EAB=√E2A+E2A+2EAEA(−12)=√E2A+E2A−E2A=EA
- Similarly, the resultant of EAB and EC will also be zero because they are equal in magnitude and symmetrically opposite.
- The electric fields due to the three charges at the centroid O cancel each other out.
- Therefore, the net electric field intensity at the centroid O is:
EO=0
The electric field intensity at the centroid of the triangle is 0.
Similar Questions
Knowledge Check
Three masses each of mass m are palced at the vertices of an equilateral triangles ABC of side l as shown in figure. The force acting on a mass 2m placed at the centroid O of the triangle is
 AzeroB3Gm2l2C5Gm2l2D7Gm2l2
AzeroB3Gm2l2C5Gm2l2D7Gm2l2
ABC is an equilateral triangle. Charges +q are placed at each corner. The electric field intensity at the centroid of triangle will be
View SolutionThree equal charges, each +q are placed on the corners of an equilatreal triangel . The electric field intensity at the centroid of the triangle is
View SolutionConsider three charges q,−q, (in Sl units) at the vetrices of an equilateral triangle with side length b. The magnitude of electric field at the centroid of the triangle is :
View SolutionThree identical charges, each having a value 1.0×10−8C, are placed at the corners of an equilateral triangle of side 20 cm find the electric field and potential at the centre of the triangle.
View SolutionConsider two charges +q and -q placed at B and C of an equilateral triangle ABC. For this system, the total charge is zero. But the electric field (intensity) at A which is equidistant from B and C is not zero. Why?
View SolutionTwo north poles each of pole strength m and a south pole of pole strength m are placed at the three corners of an equilateral triangle of side a. The intensity of magnetic induction field strength at the centre of the triangle is
View SolutionA current of 2A is flowing in the sides of an equilateral triangle of side 9 cm. The magnetic field at the centroid of the triangle is
View Solution