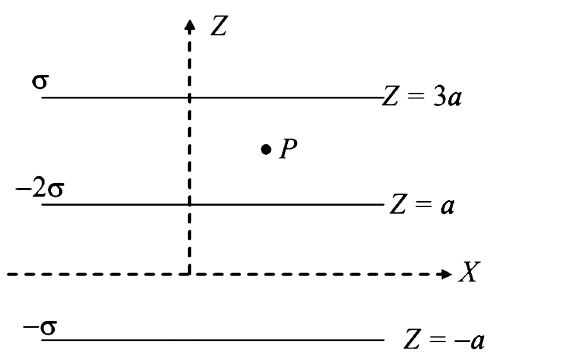
For two infinitely long charged parallel sheets, the electric feild at P will be
σ2x−σ2(r−x)
σ2ε0x+σ2π(r−x)ε0
σε0
Zero
The correct Answer is:D
To solve the problem of finding the electric field at point P between two infinitely long charged parallel sheets, we can follow these steps:
1. Understand the Configuration:
- We have two infinitely long parallel sheets, one positively charged and the other negatively charged. Let's denote the charge density of the positive sheet as σ and that of the negative sheet as −σ.
2. Electric Field Due to a Single Sheet:
- The electric field E due to an infinitely long charged sheet is given by the formula:
E=σ2ϵ0
- This electric field points away from the positively charged sheet and towards the negatively charged sheet.
3. Determine the Direction of the Electric Fields:
- For the positively charged sheet, the electric field E1 at point P (which is between the two sheets) will point away from the sheet (towards the negative sheet).
- For the negatively charged sheet, the electric field E2 at point P will point towards the sheet (also towards the negative sheet).
4. Calculate the Total Electric Field at Point P:
- Since both electric fields E1 and E2 point in the same direction (towards the negative sheet), we can add their magnitudes:
Etotal=E1+E2=σ2ϵ0+σ2ϵ0=σϵ0
5. Conclusion:
- The electric field at point P between the two sheets is:
Etotal=σϵ0
- Therefore, the electric field at point P is not zero; it has a magnitude of σϵ0 directed from the positive sheet to the negative sheet.
- We have two infinitely long parallel sheets, one positively charged and the other negatively charged. Let's denote the charge density of the positive sheet as σ and that of the negative sheet as −σ.
- The electric field E due to an infinitely long charged sheet is given by the formula:
E=σ2ϵ0
- This electric field points away from the positively charged sheet and towards the negatively charged sheet.
- For the positively charged sheet, the electric field E1 at point P (which is between the two sheets) will point away from the sheet (towards the negative sheet).
- For the negatively charged sheet, the electric field E2 at point P will point towards the sheet (also towards the negative sheet).
- Since both electric fields E1 and E2 point in the same direction (towards the negative sheet), we can add their magnitudes:
Etotal=E1+E2=σ2ϵ0+σ2ϵ0=σϵ0
- The electric field at point P between the two sheets is:
Etotal=σϵ0
- Therefore, the electric field at point P is not zero; it has a magnitude of σϵ0 directed from the positive sheet to the negative sheet.
Similar Questions
Knowledge Check
Two point charges of 1μCand−1μC are separated by a distance of 100 Å. A point P is at a distance of 10 cm from the midpoint and on the perpendicular bisector of the line joining the two charges. The electric field at P will be
A9NC−1B0.9NC−1C90NC−1D0.09NC−1Two infinite plane parallel sheets, separated by a distance d have equal and opposite uniform charge densities σ. Electric field at a point between the sheets is
Aσ2ε0Bσε0CzeroDdepends on the location of the point
An infinitely large layer of charge of uniform thickness t is placed normal to an existing uniform electric field. The charge on the sheet alters the electric field so that it still remains uniform on both the sides of the sheet and assumes values E1andE2 as shown in figure. The charge distribution in the layer is not uniform and depends only on the distance from its faces. Find the expressions for the force F per unit experienced by the charge layer.

View SolutionUse Gauss's law to derive the expression for the electric field between two uniformly charged large parallel sheets with surface charge densities σ and −σ respectively.
View SolutionConsider two infinite large parallel current carrying sheet. Current unit width in both sheets is 1√πA/m. If direction of current in both sheets is same than force per unit area on each sheet will be :
View SolutionWhat is the charge per unit area in C/m2 of an infinite plane sheet of charge if the electric field produced by the sheet of charge has magnitude 3.0N/C?
View SolutionA charge particle q is released at a distance R∘ from the infinite long wire of linear charge density λ. Then velocity will be proportional to (At distance R from the wire)
_2019_CBT2_E01_009_Q01.png)
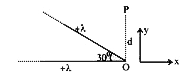
View SolutionAn infinitely long wire with linear charge density +λ is bent and the two parts are inclined at angle 30∘ as shown in fig, the electric field at point P is :
View Solution