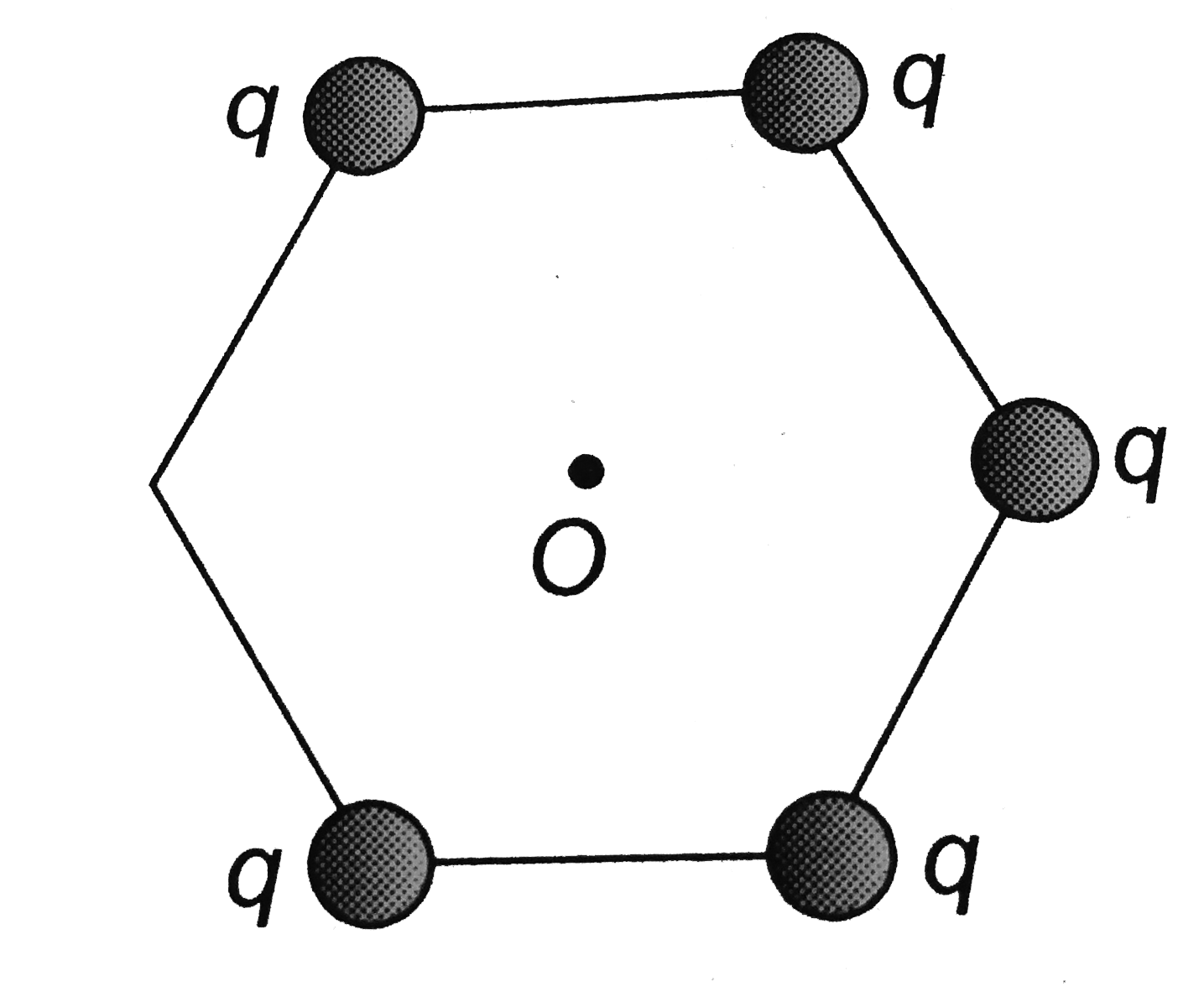
Six point charges are placed at the vertices of a hexagon of side 1 m as shown in figure. Net electric field at the centre of the hexagon is
Zero
6q4πε0
qπε0
q4πε0
The correct Answer is:C
To find the net electric field at the center of a hexagon with point charges placed at its vertices, we can follow these steps:
1. Identify the Configuration:
We have six point charges located at the vertices of a regular hexagon. Let's assume three of these charges are positive (+q) and three are negative (-q).
2. Determine the Distance to the Center:
The distance from each vertex of the hexagon to the center (O) can be calculated. For a hexagon with a side length of 1 m, the distance (r) from the center to a vertex is given by:
r=s√3=1√3 m
where s is the side length of the hexagon.
3. Calculate Electric Field Due to One Charge:
The electric field (E) due to a single point charge at a distance r is given by:
E=k⋅|q|r2
where k is Coulomb's constant. Substituting r:
E=k⋅|q|(1√3)2=3k⋅|q|
4. Consider Symmetry:
Due to the symmetry of the hexagon, the electric fields due to the positive charges will point away from the charges, while the fields due to the negative charges will point towards the charges.
5. Calculate the Net Electric Field:
The electric fields from opposite charges will cancel each other out in pairs. Thus, the net electric field at the center will be the vector sum of the fields from the three positive charges and the three negative charges.
Since the configuration is symmetrical, the net electric field can be simplified:
Enet=0
This is because the contributions from the positive and negative charges will cancel each other out perfectly.
6. Conclusion:
Therefore, the net electric field at the center of the hexagon is zero.
Final Answer:
The net electric field at the center of the hexagon is 0 N/C.
We have six point charges located at the vertices of a regular hexagon. Let's assume three of these charges are positive (+q) and three are negative (-q).
The distance from each vertex of the hexagon to the center (O) can be calculated. For a hexagon with a side length of 1 m, the distance (r) from the center to a vertex is given by:
r=s√3=1√3 m
where s is the side length of the hexagon.
The electric field (E) due to a single point charge at a distance r is given by:
E=k⋅|q|r2
where k is Coulomb's constant. Substituting r:
E=k⋅|q|(1√3)2=3k⋅|q|
Due to the symmetry of the hexagon, the electric fields due to the positive charges will point away from the charges, while the fields due to the negative charges will point towards the charges.
The electric fields from opposite charges will cancel each other out in pairs. Thus, the net electric field at the center will be the vector sum of the fields from the three positive charges and the three negative charges.
Enet=0
This is because the contributions from the positive and negative charges will cancel each other out perfectly.
Therefore, the net electric field at the center of the hexagon is zero.
The net electric field at the center of the hexagon is 0 N/C.
Similar Questions
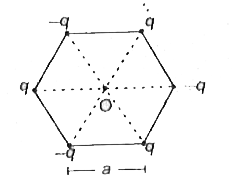
Six point charges are placed at the vertices of a regular hexagon of side a as shown. If E represents electric field and V represents electric potential at O then,
View SolutionFive point charge (+q each) are placed at the five vertices of a regular hexagon of side 2a.what is the magnitude of the net electric field at the centre of the hexazon?
View Solution
Knowledge Check
Six point charges are arrange at the vertices of a regular hexagon of side length a (shown in figure).
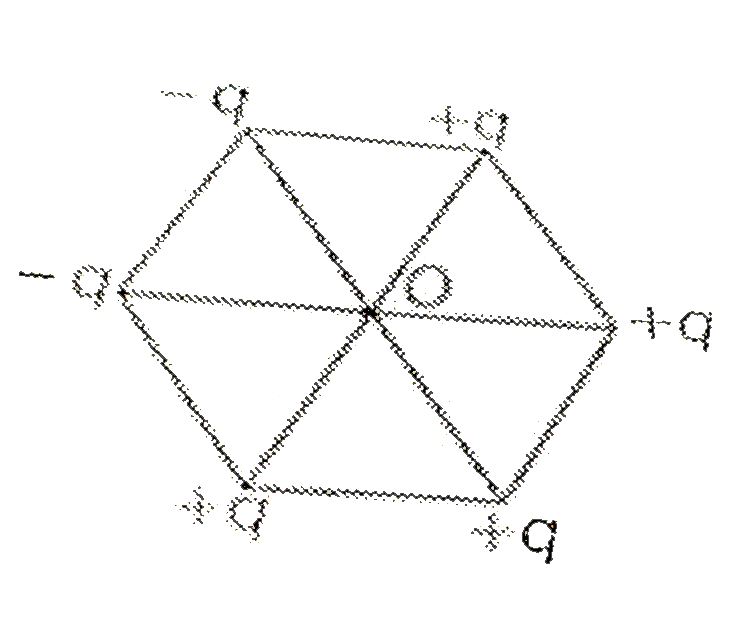
Find the magnitude of electric field at the centre of regular hexagon.A−qB−q6C+1.83qD−1.83q
Six charges are placed at the vertices of a rectangular hexagon as shown in the figure. The electric field on the line passing through point O and perpendicular to the plane of the figure as a function of distance x from point O is (assume x>>>a)

View SolutionFive point charge each having magnitudes q are placed at the corner of hexagon as shown in figure. Net electric field at the centre 'O' is →E. To get net electric field at 'O' be 6→E, charge placed on the remaining sixth corner should be
View SolutionFour charges are arranged at the corners of a square as shown in the figure. The direction of electric field at the centre of the square is along

View SolutionFive equal charges each of value q are placed at the corners of a regular pentagon of side a. The electric field at the centre of the pentagon is

View Solution3 charges are placed in a circle of radius d as shown in figure. Find the electric field along x-axis at centre of circle.

View Solution3 charges are placed in a circle of radius d as shown in figure. Find the electric field along x-axis at centre of circle.

View SolutionFour point charges are placed at the corners of a square ABCD of side 10 cm, as shown in figure. The force on a charge of 1μC placed at the centre of square is

View Solution
