In example 9 if B is the mid point of rod then find $e_{O B} \leq_{B A}$

Video Solution

Text Solution

Verified by Experts

$e_{O B} = \frac{1}{2} B ω (\frac{l^{2}}{4}) = B ω l^{2}$
$e_{B A} = \frac{1}{2} B ω {(x^{2})}_{\frac{l}{2}}^{2} = \frac{1}{2} B ω \times \frac{3 l^{2}}{4} = \frac{3}{8} B ω l^{2}$
$∴ \frac{e_{O B}}{e_{B A}} = \frac{1}{3}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Similar Questions

A(6,1) , B (8,2) and C (9,4) are three vertices of a parallelogram ABCD . If E is the mid - point of DC , then find the area of $△$ ADE.
View Solution
$A (6, 1), B (8, 2) and C (9, 4)$ are three vertices of parallelogram ABCD. If E is the mid-point of DC, then find the area of $Δ A D E$ .
View Solution
In a $△ O A B$ ,E is the mid point of OB and D is the point on AB such that $A D : D B = 2 : 1$ If OD and AE intersect at P then determine the ratio of $O P : P D$ using vector methods
View Solution
Rod $P Q$ of length $2 l$ is rotating about one end $P$ in a uniform magnetic field $B$ which is perpendicular to the plane of rotation of the rod . Point $M$ is the mid- point of the rod. Find the induced emf between $M$ and $Q$ if the potential between $P$ and $Q$ is $100 V$ .

View Solution
Rod $P Q$ of length $2 l$ is rotating about one end $P$ in a uniform magnetic field $B$ which is perpendicular to the plane of rotation of the rod . Point $M$ is the mid- point of the rod. Find the induced emf between $M$ and $Q$ if the potential between $P$ and $Q$ is $100 V$ .

View Solution
$D$ is the mid-point of side $B C$ of $△ A B C$ and $E$ is the mid-point of $B D$ . If $O$ is the mid-point of $A E$ , prove that $a r (△ B O E) = \frac{1}{8} a r (△ A B C)$ .
View Solution
In an equilateral triangle ABC , D is the mid-point of AB and E is the mid-point of AC. Find the ratio between ar ( $△ A B C) : a r (△ A D E)$
View Solution
$A B C$ is a triangle in which $D$ is the mid-point of $B C$ and $E$ is the mid-point of $A D$ . Prove that area of $△ B E D = \frac{1}{4} a r e a o f △ A B C$ . GIVEN : A $△ A B C, D$ is the mid-point of $B C$ and $E$ is the mid-point of the median $A D$ . TO PROVE : $a r (△ B E D) = \frac{1}{4} a r (△ A B C) .$
View Solution
If $A = (1, 2, 3), B = (4, 5, 6), C = (7, 8, 9)$ and D, E, F are the mid points of the triangle ABC, then find the centroid of the triangle DEF.
View Solution
ABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF, prove that $a r (Δ A E R) = a r (Δ A F R)$ .

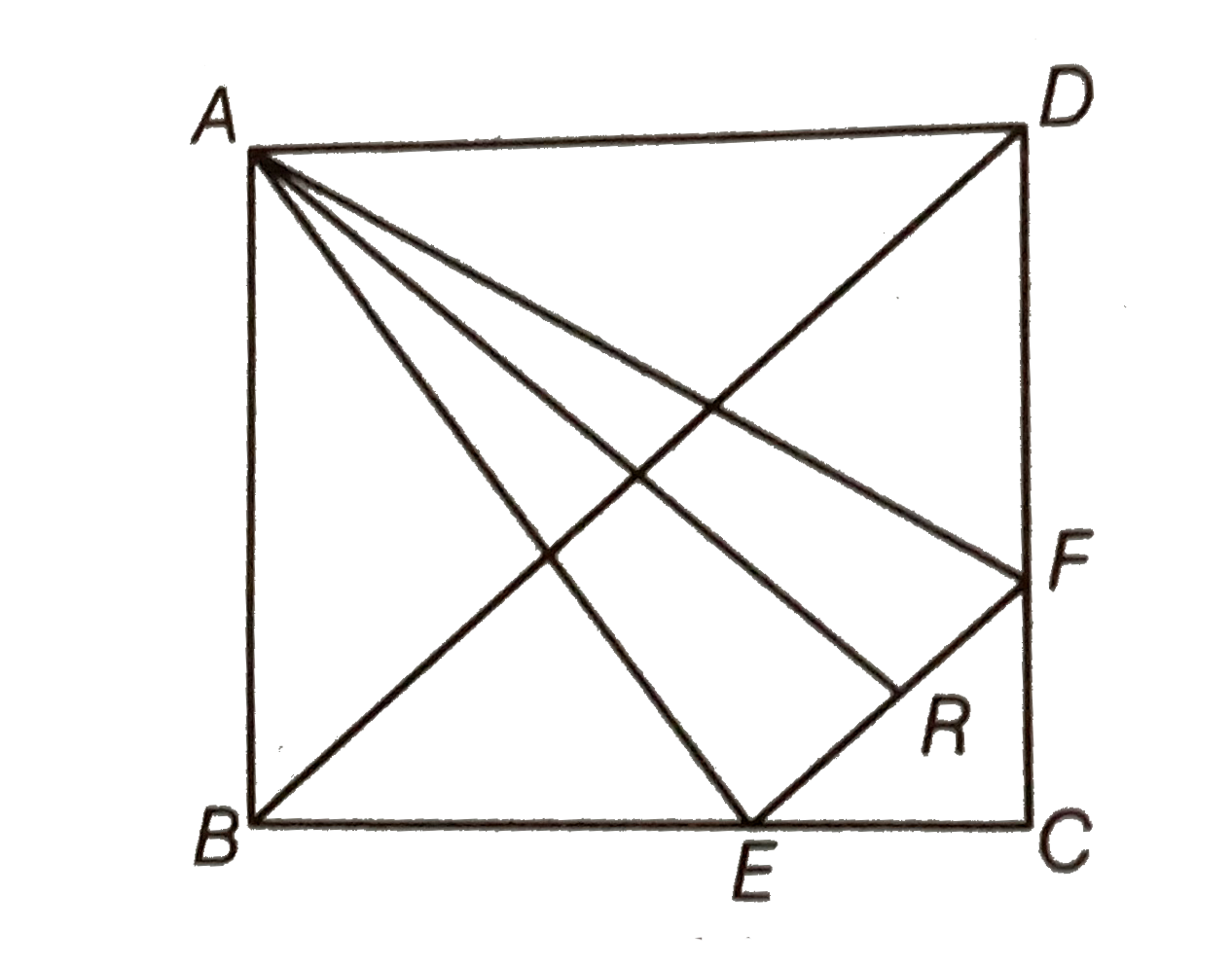View Solution

Recommended Questions

Home
Ask Doubt
Profile