If the frequency of applied source is increased, how will brightness change?
To solve the question of how the brightness changes when the frequency of the applied source is increased, we can follow these steps:
Step 1: Understand the Circuit Configuration
We have a circuit that consists of a bulb (which can be considered as a resistive load) connected in series with an inductor.
Hint: Identify the components of the circuit and their arrangement.
Step 2: Define Impedance
The total impedance (Z) of the circuit is defined as:
Z=√R2+X2L
where R is the resistance and XL is the inductive reactance.
Hint: Recall the formula for impedance in an R-L circuit.
Step 3: Express Inductive Reactance
The inductive reactance (XL) is given by:
XL=ωL=2πfL
where f is the frequency and L is the inductance.
Hint: Remember that inductive reactance depends on frequency.
Step 4: Analyze the Effect of Increasing Frequency
When the frequency (f) is increased, the inductive reactance (XL) also increases because XL is directly proportional to f.
Hint: Consider how changes in frequency affect reactance.
Step 5: Determine the Change in Impedance
As XL increases, the total impedance Z of the circuit also increases since it is a part of the impedance formula.
Hint: Think about how increasing one component in the impedance formula affects the overall impedance.
Step 6: Relate Impedance to Power and Brightness
The power (P) consumed in the circuit can be expressed as:
P=V2Z
where V is the voltage across the circuit. As Z increases, the power P decreases.
Hint: Remember that brightness of the bulb is related to the power consumed by it.
Step 7: Conclude the Effect on Brightness
Since the power decreases as the impedance increases, the brightness of the bulb will also decrease.
Hint: Summarize how changes in power relate to brightness.
Final Conclusion
When the frequency of the applied source is increased, the brightness of the bulb decreases.
---
We have a circuit that consists of a bulb (which can be considered as a resistive load) connected in series with an inductor.
The total impedance (Z) of the circuit is defined as:
Z=√R2+X2L
where R is the resistance and XL is the inductive reactance.
The inductive reactance (XL) is given by:
XL=ωL=2πfL
where f is the frequency and L is the inductance.
When the frequency (f) is increased, the inductive reactance (XL) also increases because XL is directly proportional to f.
As XL increases, the total impedance Z of the circuit also increases since it is a part of the impedance formula.
The power (P) consumed in the circuit can be expressed as:
P=V2Z
where V is the voltage across the circuit. As Z increases, the power P decreases.
Since the power decreases as the impedance increases, the brightness of the bulb will also decrease.
When the frequency of the applied source is increased, the brightness of the bulb decreases.
Similar Questions
If number of turns in the coil is increased, how will brightness change ?
View SolutionConsider an ac circuit where an incandescent light bulb is in series with an inductor. If the frequency of generator is increased, what will happen to the brightness of bulb ?
View SolutionTwo similar bulbs of wattage 100W/50√2V are connected in circuit as shown when frequency of source is varies, brightness of B2 changes it is observed that at 50 Hz frequency both the bulbs have same brightness. Select correct alternative/s
 View Solution
View SolutionA given LCR series circuit satisfes the condition for resonance with a given AC source. If the angular frequency of the AC source is increased by 100% then in order to establish resonance, and without changing the value of inductance, capacitance must be
View SolutionA given LCR series circuit satisfes the condition for resonance with a given AC source. If the angular frequency of the AC source is increased by 100% then in order to establish resonance, and without changing the value of inductance, capacitance must be
View SolutionFrequency of a character increase when it is
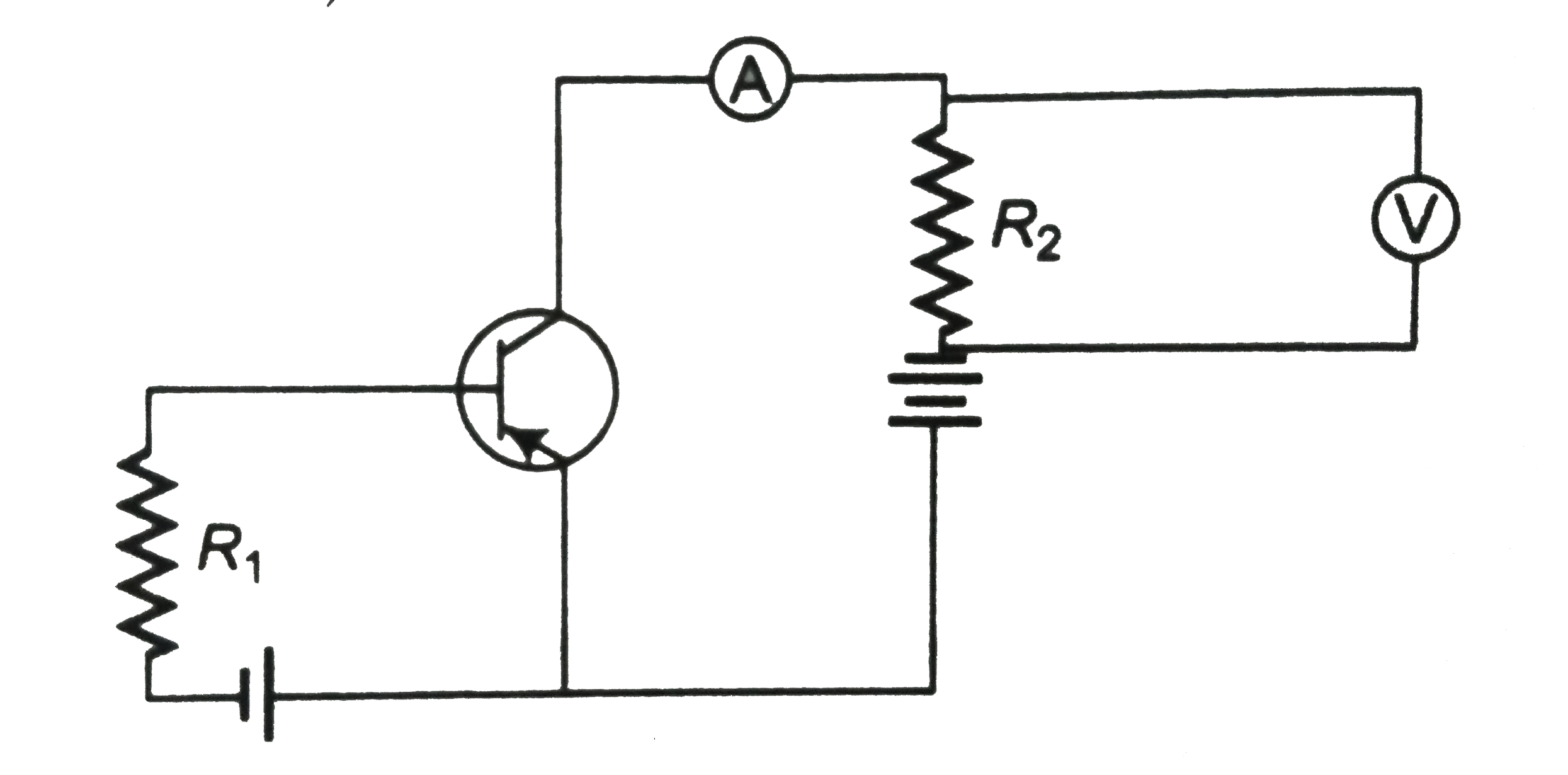
View SolutionIf the resistance R1 is increased , how will the readings of the ammeter and voltmeter change?
 View Solution
View SolutionAn a.c. source of angular frequency ω is fed across a resistor R and a capacitor C in series. The current registered is I. If now the frequency of the source is changed to ω/3 (but maintaining the same voltage), the current in the circuit is found to be halved. calculate the ratio of reactance to resistance at the original frequency ω.
View SolutionIncrease in frequency of urination is
View SolutionAn AC voltage source is applied across an R-C circuit. Angular frequency of the source is ω, resistance is R and capacitance is C. The current registered is I. If now the frequency of source is changed to ω2 (but maintaining the same voltage), the current in the circuit is found to be two third. calculate the ratio of reactance to resistance at the original frequency ω .
View Solution

