If instantaneous current in a circuit is given by A, then the effective value of resulting current in the circuit is
A
A
A
The correct Answer is:A
To find the effective (RMS) value of the instantaneous current given by I(t)=2+3sin(ωt) A, we will follow these steps:
Step 1: Understand the formula for RMS current
The effective (RMS) value of a current I(t) over one complete cycle is given by:
Irms=√1T∫T0I2(t)dt
where T is the period of the function.
Step 2: Determine the period T
The function sin(ωt) has a period of T=2πω.
Step 3: Substitute I(t) into the formula
We need to calculate I2(t):
I(t)=2+3sin(ωt)
I2(t)=(2+3sin(ωt))2=4+12sin(ωt)+9sin2(ωt)
Step 4: Integrate I2(t) over one period
Now we can calculate the integral:
∫T0I2(t)dt=∫T0(4+12sin(ωt)+9sin2(ωt))dt
This can be split into three separate integrals:
∫T04dt+∫T012sin(ωt)dt+∫T09sin2(ωt)dt
Step 5: Calculate each integral
1. First integral:
∫T04dt=4T=4⋅2πω=8πω
2. Second integral:
∫T012sin(ωt)dt=0(since the integral of sin over a full period is zero)
3. Third integral:
Using the identity sin2(θ)=1−cos(2θ)2:
∫T09sin2(ωt)dt=9∫T01−cos(2ωt)2dt=92(T−0)=92⋅2πω=9πω
Step 6: Combine the results
Now we can combine the results of the integrals:
∫T0I2(t)dt=8πω+0+9πω=17πω
Step 7: Substitute back into the RMS formula
Now we substitute this back into the RMS formula:
Irms=√1T∫T0I2(t)dt=√12πω⋅17πω=√17ω2
Step 8: Final result
Thus, the effective value of the resulting current in the circuit is:
Irms=√172 A
The effective (RMS) value of a current I(t) over one complete cycle is given by:
Irms=√1T∫T0I2(t)dt
where T is the period of the function.
The function sin(ωt) has a period of T=2πω.
We need to calculate I2(t):
I(t)=2+3sin(ωt)
I2(t)=(2+3sin(ωt))2=4+12sin(ωt)+9sin2(ωt)
Now we can calculate the integral:
∫T0I2(t)dt=∫T0(4+12sin(ωt)+9sin2(ωt))dt
This can be split into three separate integrals:
∫T04dt+∫T012sin(ωt)dt+∫T09sin2(ωt)dt
1. First integral:
∫T04dt=4T=4⋅2πω=8πω
∫T012sin(ωt)dt=0(since the integral of sin over a full period is zero)
Using the identity sin2(θ)=1−cos(2θ)2:
∫T09sin2(ωt)dt=9∫T01−cos(2ωt)2dt=92(T−0)=92⋅2πω=9πω
Now we can combine the results of the integrals:
∫T0I2(t)dt=8πω+0+9πω=17πω
Now we substitute this back into the RMS formula:
Irms=√1T∫T0I2(t)dt=√12πω⋅17πω=√17ω2
Thus, the effective value of the resulting current in the circuit is:
Irms=√172 A
Similar Questions
The current I in the circuit is

View SolutionThe current in the given circuit is
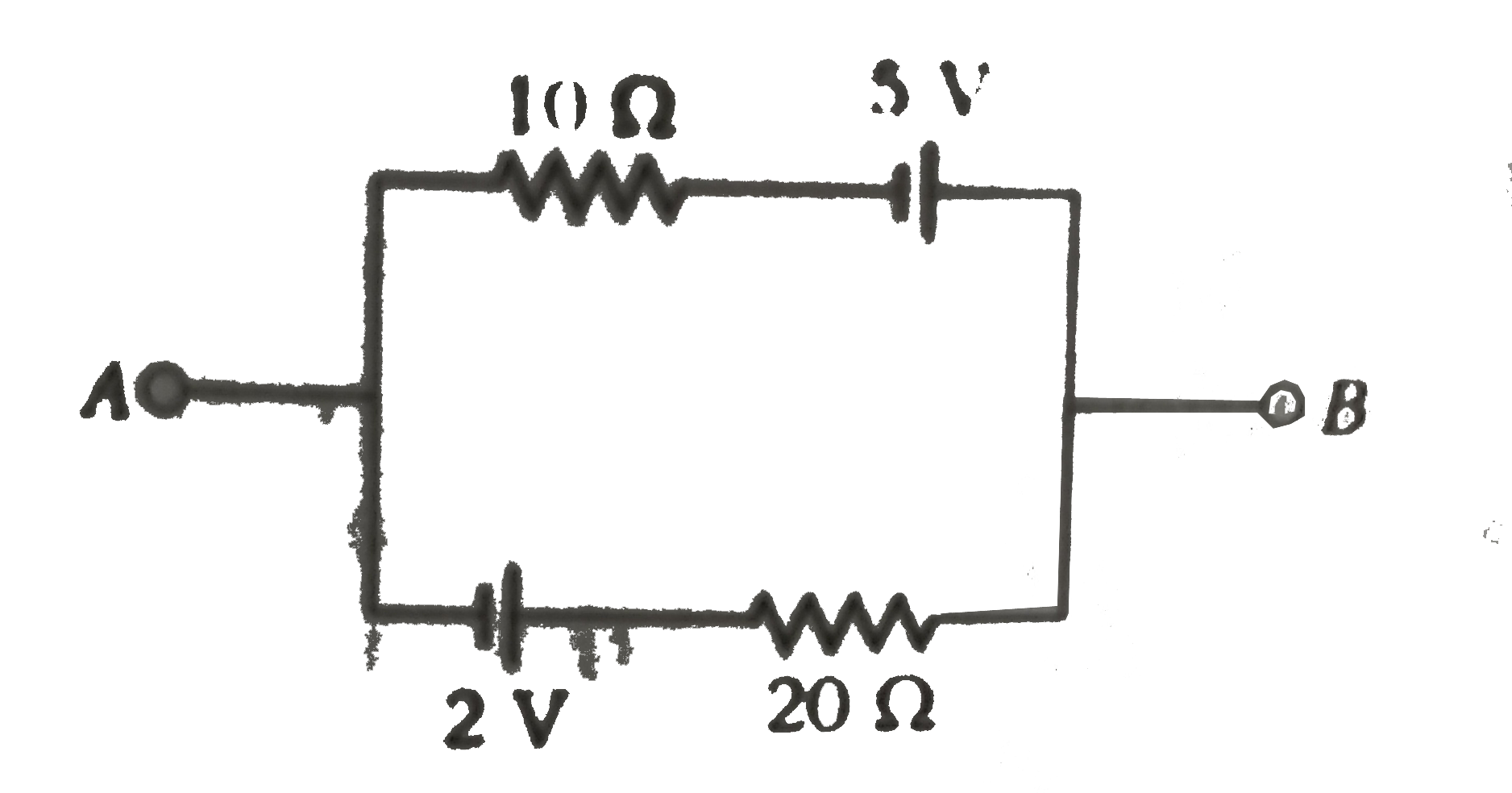
View SolutionThe value of current I in the circuit will be
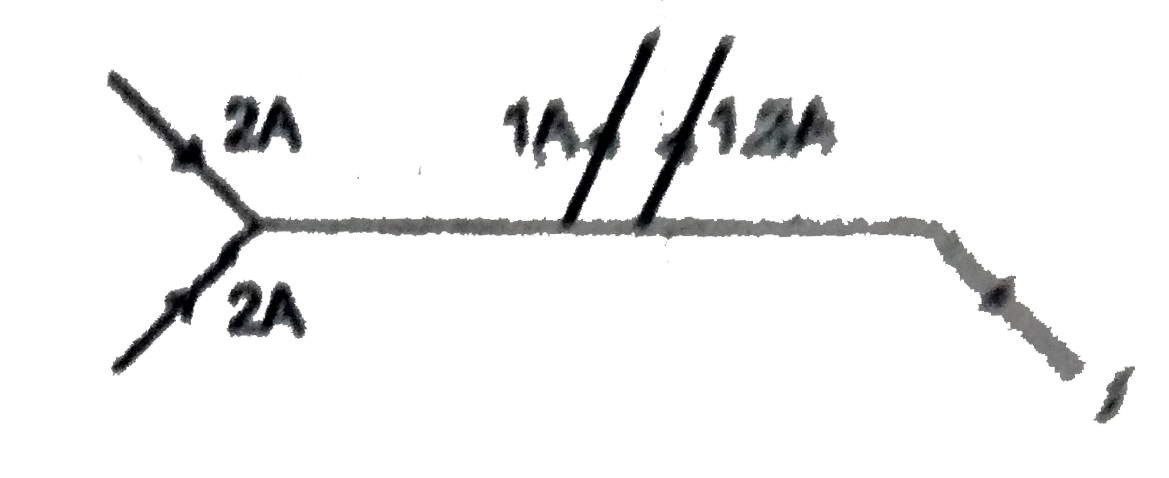
View SolutionThe current I shown in the circuit is
View SolutionCurrent in an ac circuit is given by I=3sinωt+4cosωt, then
View SolutionThe value of current i1 in the given circuit is
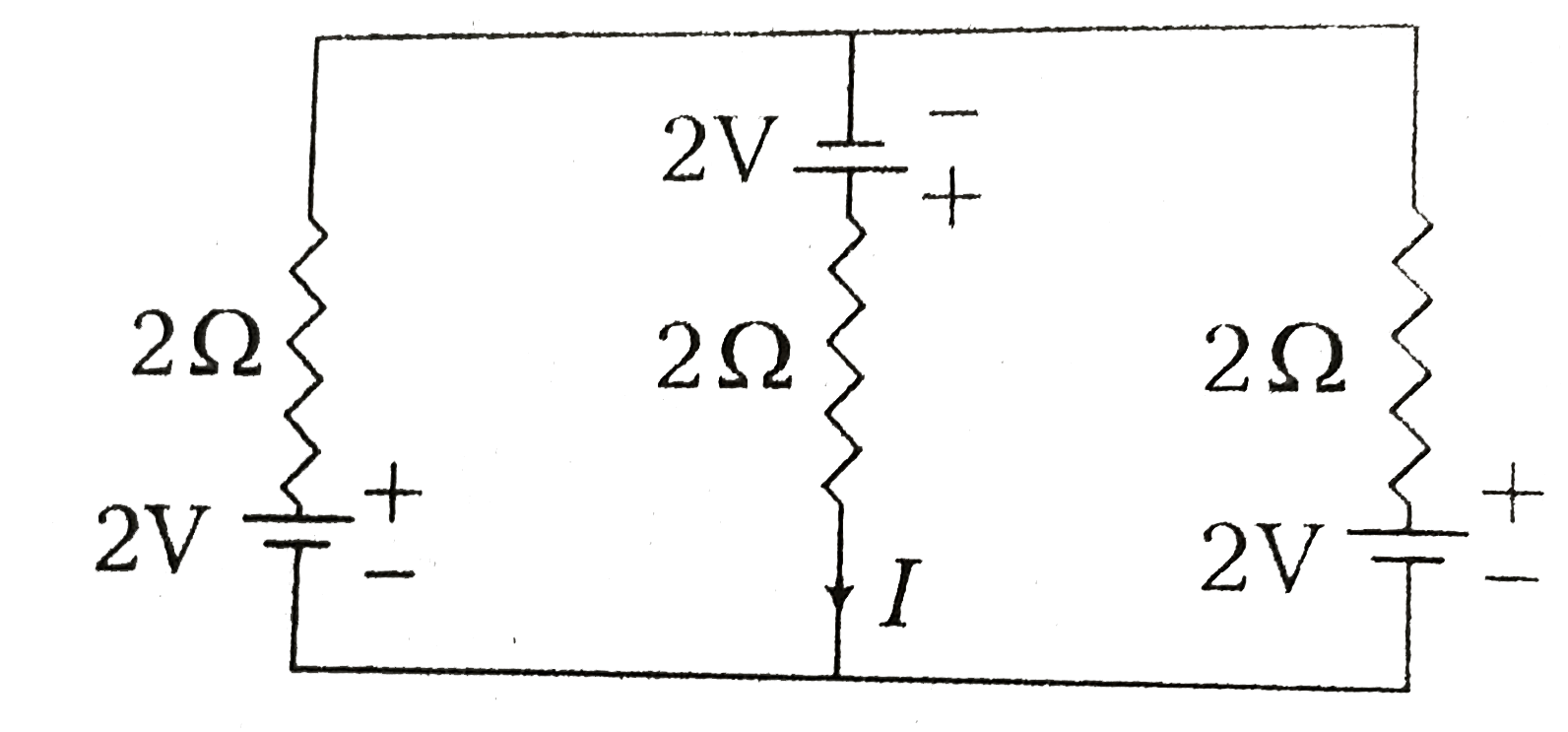
View SolutionValue of current i in the follwing circuit is:
View SolutionAn AC current is given by i= 3+4 sinwt ,then its effective value
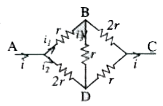
View SolutionWhat is value of current I in given circuit
View SolutionWhat is the value of current I in given circuits
(a)_S01_050_Q01.png)
View Solution
