If the power factor in an AC circuit changes from 13 to 19 then by what percent reactance will change (approximately), If resistance remains constant?
Increase by 200%
Decrease by 200%
Increased by 100%
Decrease by 100%
The correct Answer is:A
To solve the problem, we need to find the percentage change in reactance when the power factor changes from 13 to 19, while keeping the resistance constant.
1. Understanding Power Factor:
The power factor (PF) is defined as:
PF=cos(ϕ)
where ϕ is the phase angle between the voltage and current.
2. Calculate the Angles:
For the initial power factor of 13:
cos(ϕ1)=13⟹ϕ1=cos−1(13)
For the new power factor of 19:
cos(ϕ2)=19⟹ϕ2=cos−1(19)
3. Relate Reactance to Resistance and Angle:
The reactance X can be expressed as:
X=Rtan(ϕ)
Therefore, we can express the reactance for both cases:
X1=Rtan(ϕ1)
X2=Rtan(ϕ2)
4. Calculate Tangent Values:
Using the identity tan(ϕ)=sin(ϕ)cos(ϕ) and knowing sin2(ϕ)+cos2(ϕ)=1:
- For ϕ1:
sin(ϕ1)=√1−(13)2=√1−19=√89=2√23
tan(ϕ1)=sin(ϕ1)cos(ϕ1)=2√2313=2√2
- For ϕ2:
sin(ϕ2)=√1−(19)2=√1−181=√8081=4√59
tan(ϕ2)=sin(ϕ2)cos(ϕ2)=4√5919=4√5
5. Calculate Reactance Values:
Now we can find the reactance values:
X1=R⋅2√2
X2=R⋅4√5
6. Calculate Percentage Change:
The percentage change in reactance is given by:
Percentage Change=X2−X1X1×100
Substituting the values:
Percentage Change=R⋅4√5−R⋅2√2R⋅2√2×100
Simplifying this:
=4√5−2√22√2×100=(24√5−2√22√2)×100
=(24√52√2−1)×100=(2√10−1)×100
Approximating √10≈3.16:
=(6.32−1)×100≈532%
Final Answer:
The percentage change in reactance is approximately 200%.
The power factor (PF) is defined as:
PF=cos(ϕ)
where ϕ is the phase angle between the voltage and current.
For the initial power factor of 13:
cos(ϕ1)=13⟹ϕ1=cos−1(13)
For the new power factor of 19:
cos(ϕ2)=19⟹ϕ2=cos−1(19)
The reactance X can be expressed as:
X=Rtan(ϕ)
Therefore, we can express the reactance for both cases:
X1=Rtan(ϕ1)
X2=Rtan(ϕ2)
Using the identity tan(ϕ)=sin(ϕ)cos(ϕ) and knowing sin2(ϕ)+cos2(ϕ)=1:
- For ϕ1:
sin(ϕ1)=√1−(13)2=√1−19=√89=2√23
tan(ϕ1)=sin(ϕ1)cos(ϕ1)=2√2313=2√2
- For ϕ2:
sin(ϕ2)=√1−(19)2=√1−181=√8081=4√59
tan(ϕ2)=sin(ϕ2)cos(ϕ2)=4√5919=4√5
Now we can find the reactance values:
X1=R⋅2√2
X2=R⋅4√5
The percentage change in reactance is given by:
Percentage Change=X2−X1X1×100
Substituting the values:
Percentage Change=R⋅4√5−R⋅2√2R⋅2√2×100
Simplifying this:
=4√5−2√22√2×100=(24√5−2√22√2)×100
=(24√52√2−1)×100=(2√10−1)×100
=(6.32−1)×100≈532%
The percentage change in reactance is approximately 200%.
Similar Questions
The power factor of an AC circuit having resistance (R) and inductance (L) connected in series and an angular velocity ω is
View SolutionThe power factor of an R-L circuit is 1/√2 if the frequency of AC is doubled , what will be the power
View SolutionIf a copper wire is stretched to make it 0.1% longer, then the percentage change in resistance is approximately -
View SolutionThe power factor of the circuit in fig. is 1/√2. The capacitance of the circuit is equal to
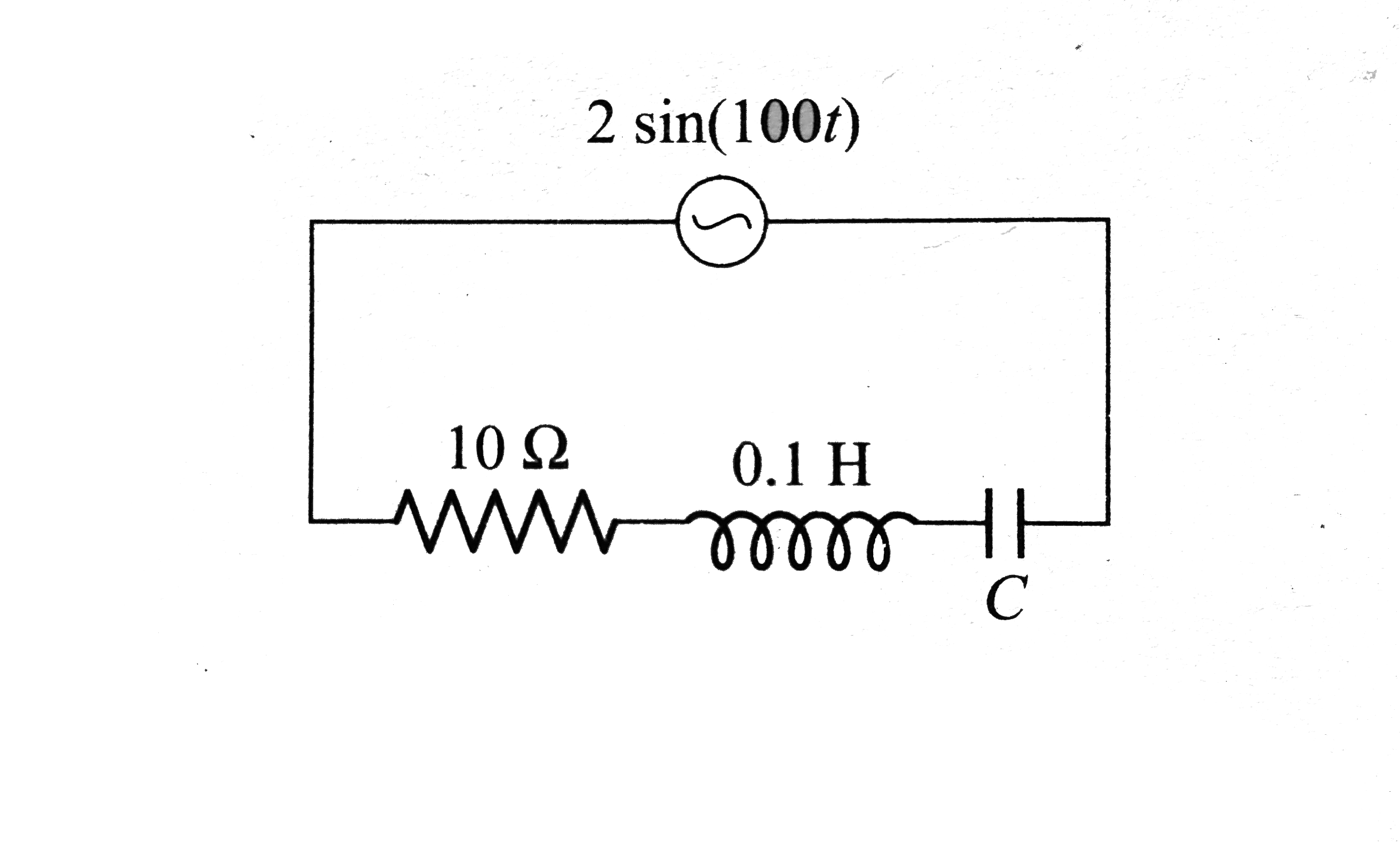
View SolutionIf y=sinxandx change from π2→2214, what is the approximate change in y?
View SolutionIf y=sinx and x changes from π/2 to 22/14 , what is the approximate change in y ?
View SolutionA choke coil is connected to an AC source. Some power is dissipated in coil. Now a capacitor is connected in series with the coil and source is same, then average power dissipated in the circuit does not changes. If ratio of inductive reactance of coil and capacitive reactance of capacitor is1x then find x
View SolutionPower factor of an L-R series circuit is 0.6 and that of a C-R series circuit is 0.5. If the element (L. C, and R) of the two circuits are joined in series the power factor of this circuit is found to be 1. The ratio of the resistance in the L-R circuit to the resistance in the C-R circuit is
View SolutionIn a RLC circuit capacitance is changed from C to 2 C. For the resonant frequency to remain unchanged, the inductance should be changed from L to
View SolutionAs the ray of light passes from air to glass , state how the wavelength of light changes does it increase , decrease or remain constant ?
View Solution
