Two optical media of refractive indices n1 and n2 contain x and y waves of the same colour in the same thickness. Then their relative refractive index n1/n2
xy
yx
xy
y−xx
The correct Answer is:B
To find the relative refractive index n1n2 of two optical media containing waves of the same color, we can follow these steps:
Step 1: Understand the relationship between refractive index and wave properties
The refractive index n of a medium is defined as:
n=cv
where c is the speed of light in vacuum and v is the speed of light in the medium.
Step 2: Relate speed of light to wavelength and frequency
The speed of light in a medium can also be expressed in terms of wavelength λ and frequency f:
v=f⋅λ
Thus, we can rewrite the refractive index in terms of wavelength:
n=cf⋅λ
Step 3: Write the relationship for both media
For the first medium with refractive index n1 and thickness x:
x=Tλn1⟹x=T⋅n1λ
For the second medium with refractive index n2 and thickness y:
y=Tλn2⟹y=T⋅n2λ
Step 4: Set the thicknesses equal
Since the thicknesses x and y are the same, we can equate the two expressions:
T⋅n1λ=T⋅n2λ
Here, T and λ cancel out, leading to:
n1=n2⋅xy
Step 5: Rearrange to find the relative refractive index
Rearranging the above equation gives us:
n1n2=xy
Conclusion
Thus, the relative refractive index n1n2 is equal to the ratio of the thicknesses of the two media:
n1n2=xy
Final Answer
The relative refractive index n1n2 is xy.
---
The refractive index n of a medium is defined as:
n=cv
where c is the speed of light in vacuum and v is the speed of light in the medium.
The speed of light in a medium can also be expressed in terms of wavelength λ and frequency f:
v=f⋅λ
Thus, we can rewrite the refractive index in terms of wavelength:
n=cf⋅λ
For the first medium with refractive index n1 and thickness x:
x=Tλn1⟹x=T⋅n1λ
For the second medium with refractive index n2 and thickness y:
y=Tλn2⟹y=T⋅n2λ
Since the thicknesses x and y are the same, we can equate the two expressions:
T⋅n1λ=T⋅n2λ
Here, T and λ cancel out, leading to:
n1=n2⋅xy
Rearranging the above equation gives us:
n1n2=xy
Thus, the relative refractive index n1n2 is equal to the ratio of the thicknesses of the two media:
n1n2=xy
The relative refractive index n1n2 is xy.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSIGNMENT (SECTION - D)
16 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSIGNMENT (SECTION - B)
35 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
- SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )EXERCISE - Assignment SECTION - D (Assertion & reason type Question)
10 Videos
Similar Questions
A biconvex thin lens is prepared from glass of refractive index μ2=32. The two conducting surfaces have equal radii of 20 cm each. One of the the surface is silvered from outside to make it reflecting. It is placed in a medium of refractive index μ1=53. It acts as a
View SolutionA light ray moving in medium-I (of refractive index n1) is incident on interface of two media and it is totally internally reflected at the interface. Now, refractive index n2 of medium-II is decreased, then

View SolutionA ray of light is incident on the left vertical face of glass cube of refractive index n2, as shown in figure. The plane of incidence is the plane of the page, and the cube is surrounded by liquid (refractive index=n1). What is the largest angle of incidence θ1 for which total internal reflection occurs at the top surfaces?

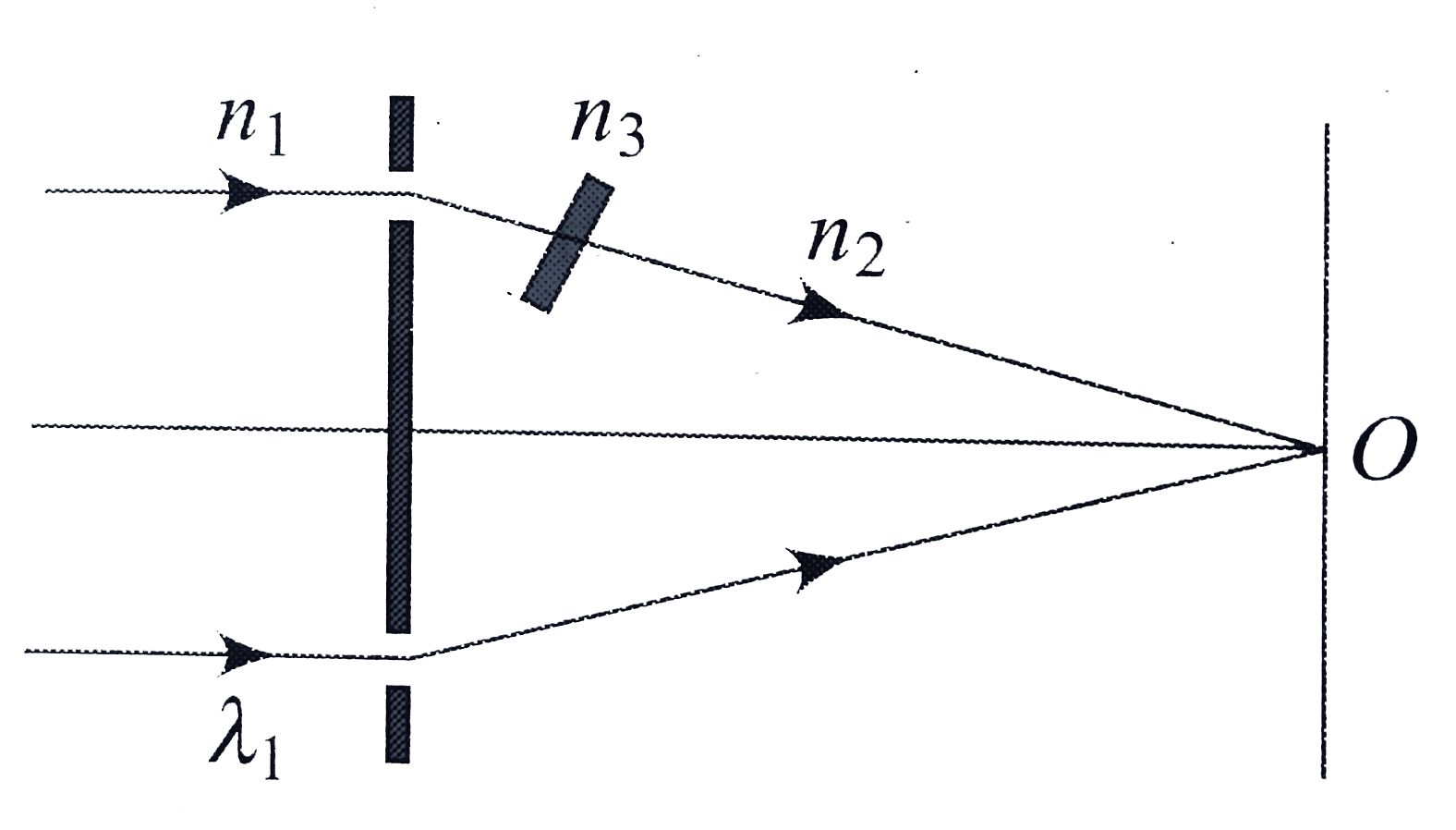
View SolutionIn YDSE shown in figure a parallel beam of light is incident on the slits from a medium of refractive index n1. The wavelength of light in this medium is λ1. A transparent slab of thickness t and refractive index n3 is put in front of one slit. The medium between the screen and the plane of the slits is n2. The phase difference between the light waves reaching point O (symmetrical, relative to the slits) is
View SolutionWhen a lens of refractive index n1, then the lens looks to be dissapeared only, if
View SolutionAn equiconvex lens of refractive index n2 is placed such that the refractive index of the surrouding media is as shown. The lens :
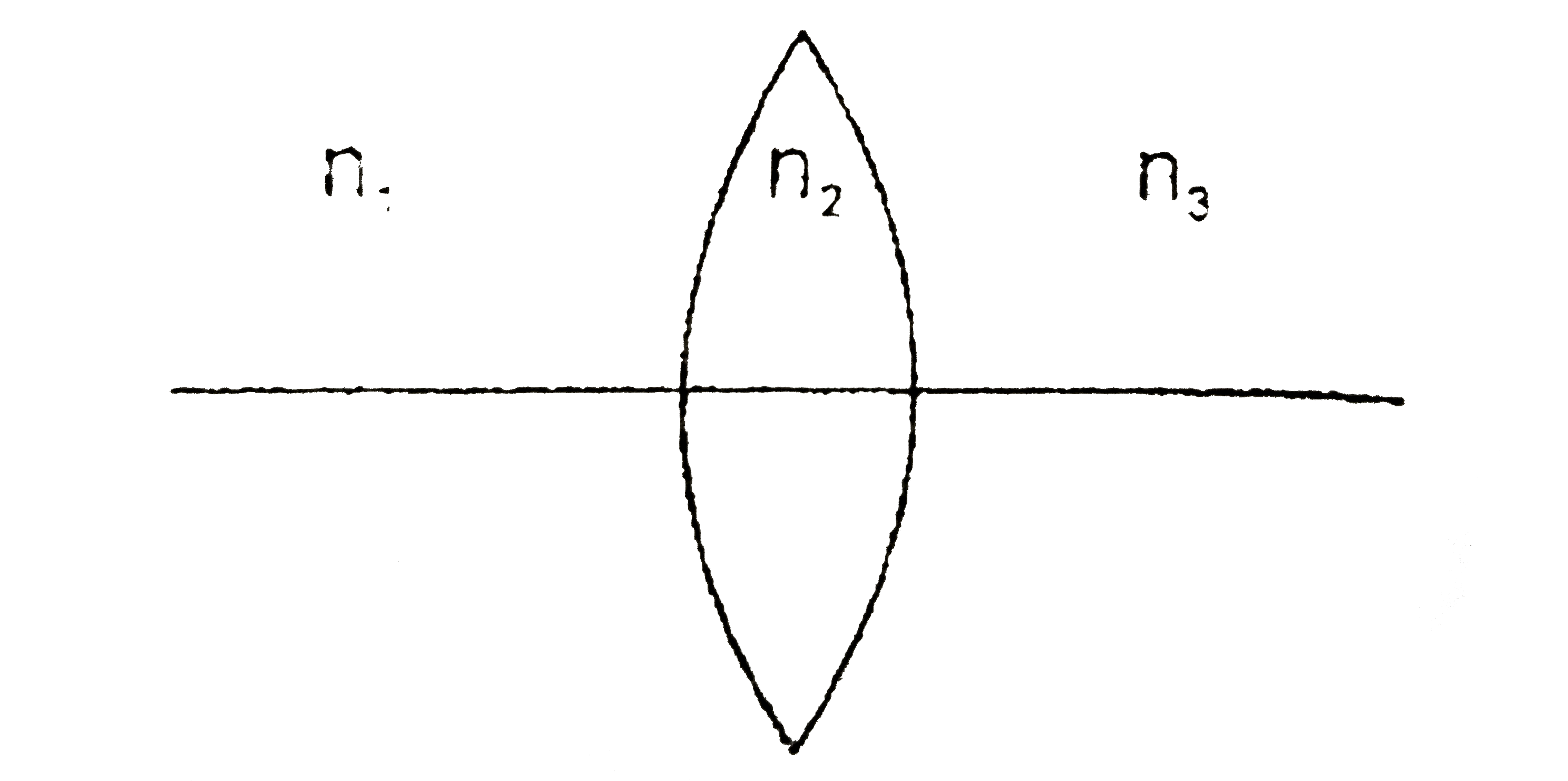
View SolutionA tranparent sphere of radius 20cm and refractive index 1.6 is fixed in a hole of the partition separating the two media: A(refractive index n1=1.2) and B ( refractive index n3=1.7). A luminous point object is placed 120cm from the surface of the sphere iin medium A. it is viewed from D in medium B in a direction normal to the sphere. Find the position of the image formed by the rays, from point N.

View SolutionThe refractive index of the material of a concave lens is n. It is immersed in a medium of refractive index n1. A paprallel beam of light is incident on the lens. Trace the path of emerged rays in each of the following cases :
(a) n1>n (b) n1<n ( c) n1=n.
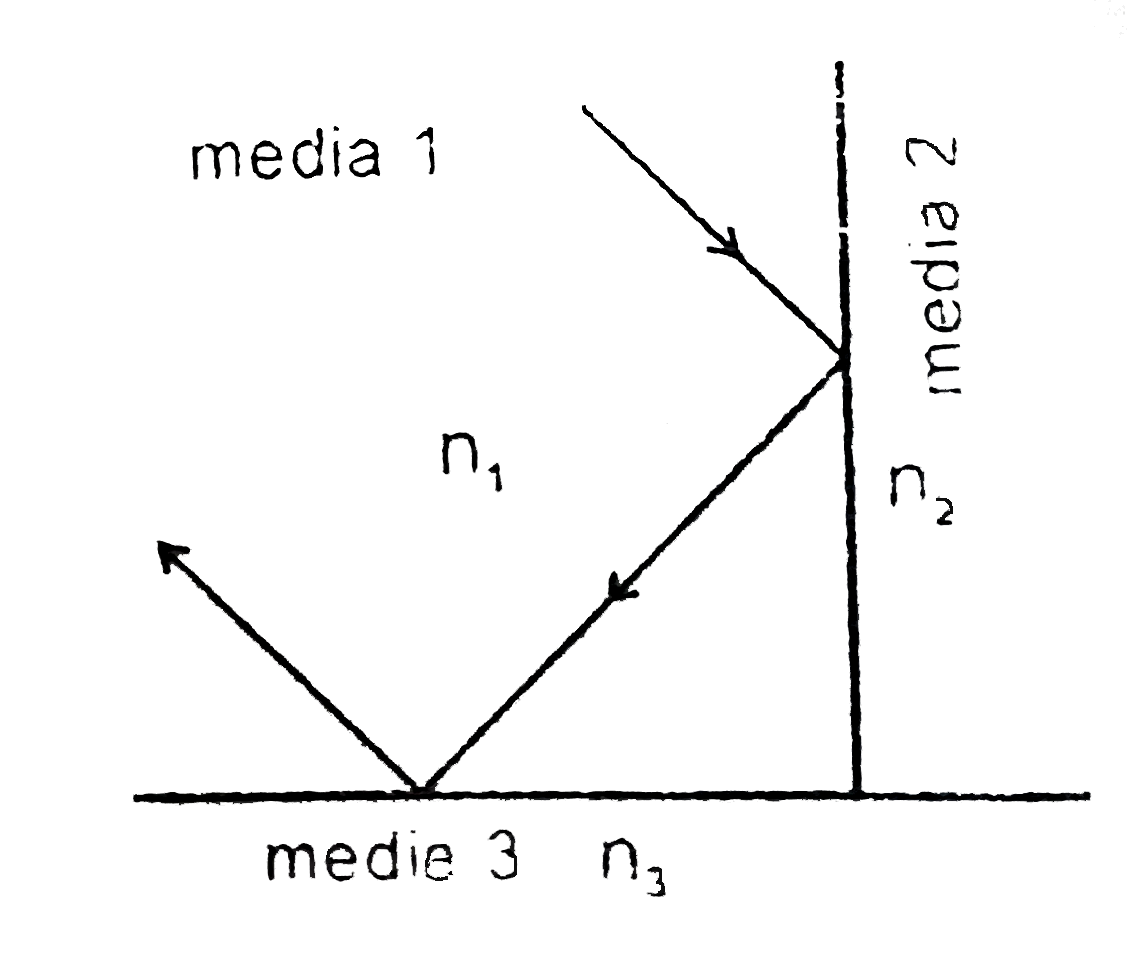
View SolutionIn the diagram shown, light is incident on the interface between media 1 (refractive index n1) and 2 (refractive index n2) at angle slightly greater than the critical angle, and is totally reflected. The light is then also totally reflected at the interface between media 1 and 3 (refractive index n3), after which it travels in a direction opposite to its initial direction, The media must have a refractive indices such that.
 .
.
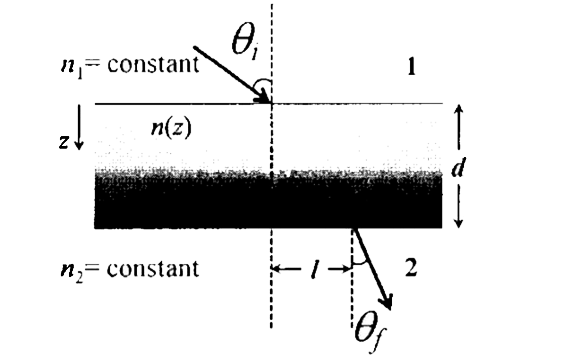
View SolutionA transparent slab of thickness d has a refractive index n(z) that increases with z. Here z is the vertical distance inside the slab, measured from the top. The slab is placed between two media with uniform refractive indices n1 and n2(>n1), θ0, from medium 1 and emerges in medium 2 with refraction angle θtwith a lateral displacement l.
Which of the following statement(s) is (are) true?
View Solution