Figure shows four situations in which an electron is moving in electric / magnetic field . In which case the de Broglie wavelength of electron is increasing ?

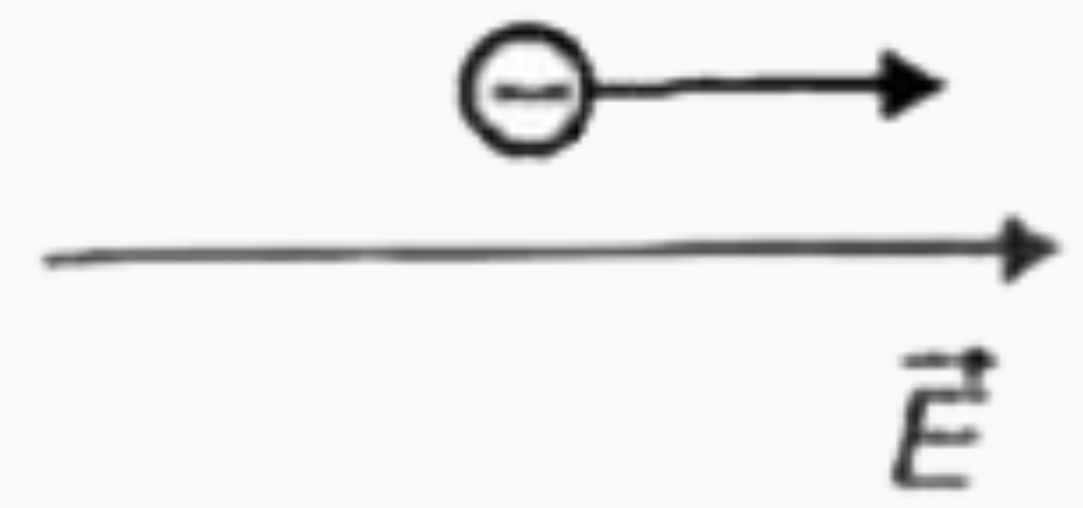
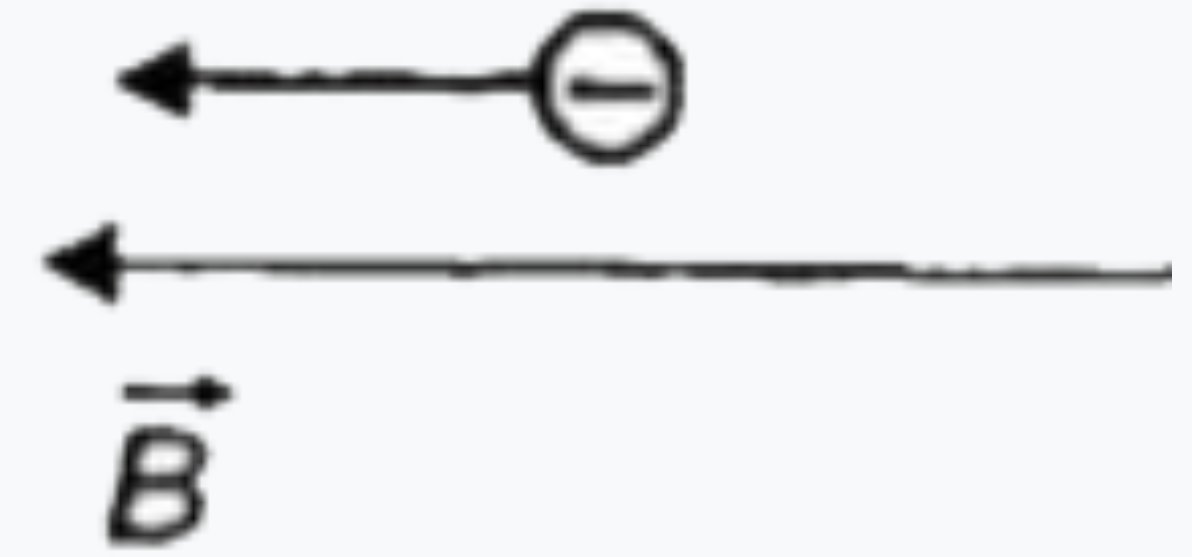
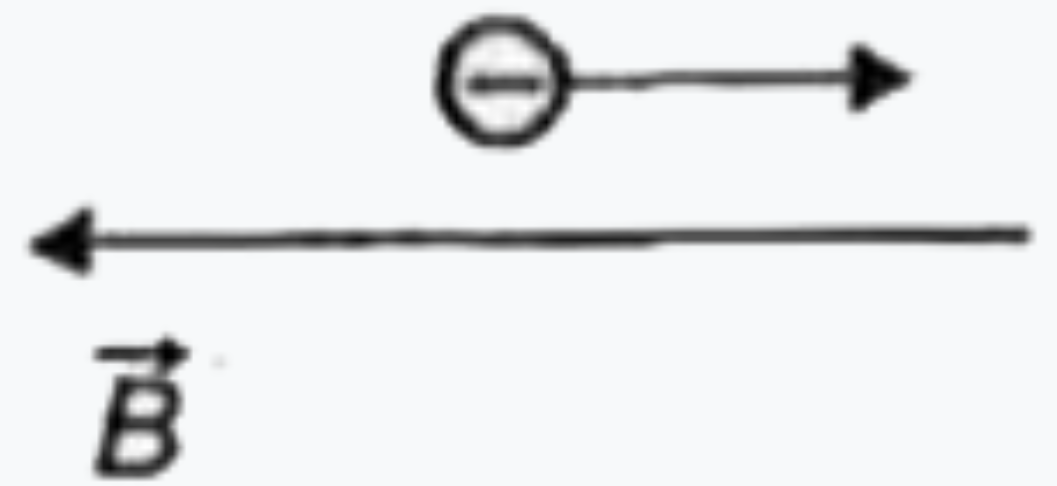
The correct Answer is:B
To determine in which case the de Broglie wavelength of an electron is increasing, we can analyze the relationship between the kinetic energy of the electron and its de Broglie wavelength. The de Broglie wavelength (λ) is given by the formula:
λ=h√2mK.E.
where:
- h is Planck's constant,
- m is the mass of the electron,
- K.E. is the kinetic energy of the electron.
From this formula, we can see that the de Broglie wavelength is inversely proportional to the square root of the kinetic energy. This means that if the kinetic energy of the electron decreases, the de Broglie wavelength will increase.
1. Identify the Relationship: Recall that the de Broglie wavelength is inversely proportional to the square root of the kinetic energy of the electron. Thus, if the kinetic energy increases, the wavelength decreases, and if the kinetic energy decreases, the wavelength increases.
2. Analyze Each Situation: For each of the four situations provided in the figure, we need to determine whether the kinetic energy of the electron is increasing or decreasing based on the forces acting on it.
3. Situation 1: If the force acting on the electron is in the same direction as the electric field, the kinetic energy of the electron will increase. Therefore, the de Broglie wavelength will decrease.
4. Situation 2: If the force acting on the electron is opposite to the direction of the electric field, the kinetic energy of the electron will decrease. Therefore, the de Broglie wavelength will increase.
5. Situation 3: Analyze the forces and directions similarly. If the force causes the electron to speed up, the kinetic energy increases, and the wavelength decreases. If the force slows it down, the kinetic energy decreases, and the wavelength increases.
6. Situation 4: Again, check the direction of the force relative to the electric field. Determine if the kinetic energy is increasing or decreasing.
7. Conclusion: After analyzing all four situations, we find that in Situation 2, the kinetic energy of the electron decreases, leading to an increase in the de Broglie wavelength.
Final Answer:
The de Broglie wavelength of the electron is increasing in Situation 2.
- h is Planck's constant,
- m is the mass of the electron,
- K.E. is the kinetic energy of the electron.
The de Broglie wavelength of the electron is increasing in Situation 2.
Topper's Solved these Questions
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Try Yourself
15 Videos
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Assignment (Section - A) ( Objective Type Questions ( One option is correct))
40 Videos
- ATOMSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ATOMSEXERCISE - ASSIGNMENT SECTION J (Aakash Challengers )
5 Videos
Similar Questions
Knowledge Check
The de-Broglie wavelength of an electron in the first Bohr orbit is
Aequal to one- fourth the circumference of the first orbitBequal to half the circumference of first orbitCequal to twice the circumference of first orbit.Dequal to the circumference of the first orbit.When the velocity of an electron increases, its de Broglie wavelength
AincreasesBdecreasesCremains sameDmay increase or decreaseIf a proton and electron have the same de Broglie wavelength, then
Akinetic energy of electron < kinetic energy of protonBkinetic energy of electron = kinetic energy of protonCmomentum of electron = momentum of protonDmomentum of electron < momentum of proton
A moving electron has 5×10−25Jof kinetic energy .What is the de Broglie wavelength ?
View SolutionAn electron is moving through a field. It is moving (i) opposite an electric field (ii) perpendicular to a magnetic field as shown. For each situation the de - Broglie wave length of electron
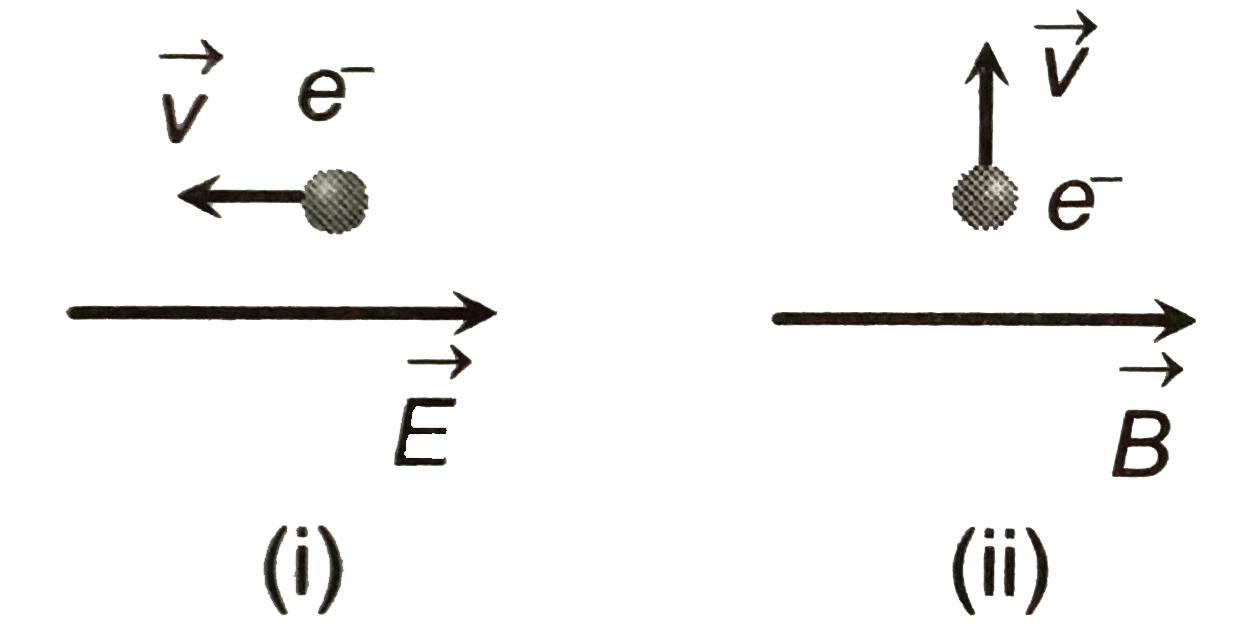
View Solutionde Broglie wavelength of electron in second orbit of Li2+ ion will be equal to de Broglie's wavelength of electron in :
View SolutionThe de-Broglie wavelength of electron in gound state of an hydrogen atom is
View SolutionA proton and an electron have same kinetic energy. Which one has greater de-Broglie wavelength and why ?
View Solution
