In Rutherford's experiment, number of particles scattered at 90∘ angel are x per second. Number particles scattered per second at angle 60∘ is
x
4x
8x
16x
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Understand the relationship between scattering angles and the number of particles.
In Rutherford's experiment, the number of particles scattered at different angles is related to the sine of half the scattering angle. Specifically, the number of particles scattered per second (N) is inversely proportional to the sine of half the angle raised to the fourth power. This can be expressed as:
N∝1sin4(ϕ/2)
Step 2: Define the variables.
Let:
- N1 be the number of particles scattered at 90∘ (which is given as x).
- N2 be the number of particles scattered at 60∘.
- ϕ1=90∘
- ϕ2=60∘
Step 3: Set up the proportionality equation.
From the relationship established, we can write:
N1N2=sin4(ϕ2/2)sin4(ϕ1/2)
Step 4: Calculate the sine values for the angles.
- For ϕ1=90∘:
sin(90∘/2)=sin(45∘)=√22
- For ϕ2=60∘:
sin(60∘/2)=sin(30∘)=12
Step 5: Substitute the sine values into the equation.
Now substituting these values into the equation gives:
xN2=(12)4(√22)4
Step 6: Simplify the equation.
Calculating the right-hand side:
- (12)4=116
- (√22)4=2216=416=14
So the equation becomes:
xN2=11614=116×4=14
Step 7: Solve for N2.
Cross-multiplying gives:
x⋅4=N2
Thus:
N2=4x
Final Answer:
The number of particles scattered per second at an angle of 60∘ is 4x.
---
In Rutherford's experiment, the number of particles scattered at different angles is related to the sine of half the scattering angle. Specifically, the number of particles scattered per second (N) is inversely proportional to the sine of half the angle raised to the fourth power. This can be expressed as:
N∝1sin4(ϕ/2)
Let:
- N1 be the number of particles scattered at 90∘ (which is given as x).
- N2 be the number of particles scattered at 60∘.
- ϕ1=90∘
- ϕ2=60∘
From the relationship established, we can write:
N1N2=sin4(ϕ2/2)sin4(ϕ1/2)
- For ϕ1=90∘:
sin(90∘/2)=sin(45∘)=√22
- For ϕ2=60∘:
sin(60∘/2)=sin(30∘)=12
Now substituting these values into the equation gives:
xN2=(12)4(√22)4
Calculating the right-hand side:
- (12)4=116
- (√22)4=2216=416=14
xN2=11614=116×4=14
Cross-multiplying gives:
x⋅4=N2
Thus:
N2=4x
The number of particles scattered per second at an angle of 60∘ is 4x.
Similar Questions
In Rutherford experiments on α-ray scattering the number of particles scattered at 900angle be 28 per minute. Then the number of particles scattered per minute by the same foil, but at 600 is
View SolutionIn the Rutherford scattering experiment the number of α particles scattered at anangle θ=60∘ is 12 per min. The number of α particles per minute when scattered at an angle of 90∘ are
View Solution
Knowledge Check
The graph of the total number of α-particles scattered at different angles in a given interval of time for α- particles scattering in the geiger- marsden experiment is given by
A B
B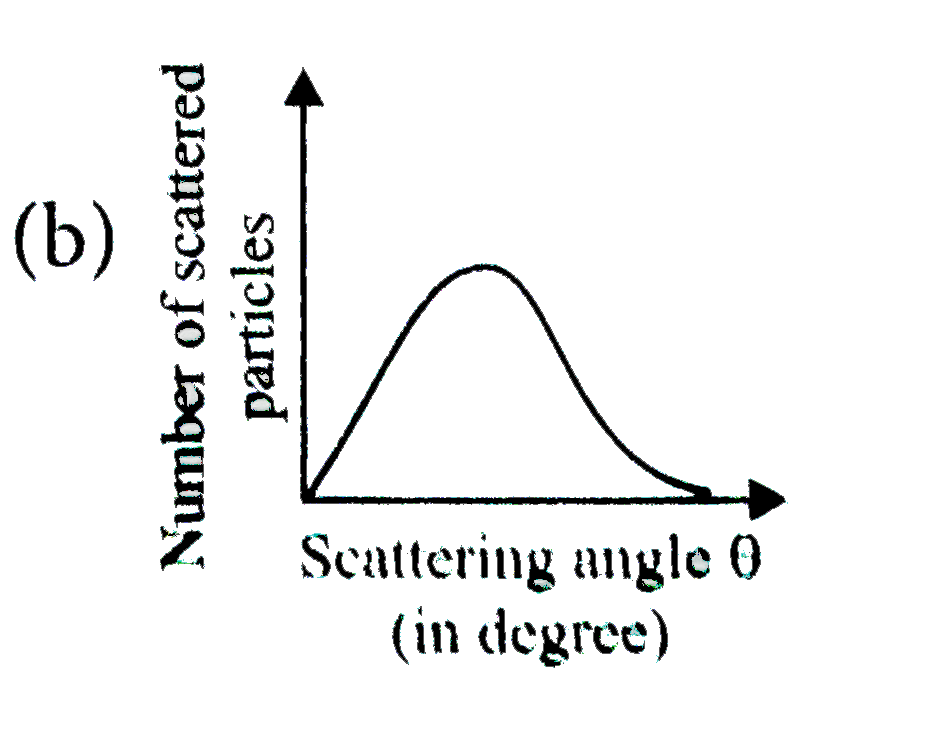 C
C D
D
In scattering experiment , α -particles were deflected by
View SolutionWhen a silver foil (Z = 47) was used in an α ray scattering experiment , the number of α-particles scattered at 30∘ was found to be 200 per minute. If the silver foil is replaced by alumninium (z = 13) foil of same thickness, the number of α-particles scattered per minute at 30∘ is nearly equal to
View SolutionIn Rutherford scattering experiment for scattering angle of 180∘, what be the value of impact parameter?
View SolutionRutherford's alpha-particle scattering experiment discovered
View SolutionRutherford's experiment on the scattering of α particle showed for the first time that the atom has
View SolutionRutherford's experiment on the scattering of α particle showed for the first time that the atom has
View SolutionIn Rutherford's alpha-rays scattering experiment, the alpha particles are detected using a screen coated with
View Solution