If force is applied on a particle along x = axis, then find the work done by it during motion of particle from x = 0 to x = 2 m.
To find the work done by the force F=(2x+3x2)N on a particle moving from x=0 to x=2m, we can follow these steps:
Step 1: Write the expression for work done
The work done W by a force when moving an object along a path is given by the integral of the force over the distance moved. Mathematically, this is expressed as:
W=∫x2x1Fdx
where F is the force and x1 and x2 are the initial and final positions.
Step 2: Substitute the force into the integral
Given F=2x+3x2, we substitute this into the work integral:
W=∫20(2x+3x2)dx
Step 3: Split the integral
We can split the integral into two parts:
W=∫202xdx+∫203x2dx
Step 4: Calculate the first integral
The first integral is:
∫2xdx=2⋅x22=x2
Evaluating from 0 to 2:
(x2)20=22−02=4−0=4
Step 5: Calculate the second integral
The second integral is:
∫3x2dx=3⋅x33=x3
Evaluating from 0 to 2:
(x3)20=23−03=8−0=8
Step 6: Combine the results
Now we can combine the results of both integrals to find the total work done:
W=4+8=12J
Final Answer
The work done by the force as the particle moves from x=0 to x=2m is:
12J
The work done W by a force when moving an object along a path is given by the integral of the force over the distance moved. Mathematically, this is expressed as:
W=∫x2x1Fdx
where F is the force and x1 and x2 are the initial and final positions.
Given F=2x+3x2, we substitute this into the work integral:
W=∫20(2x+3x2)dx
We can split the integral into two parts:
W=∫202xdx+∫203x2dx
The first integral is:
∫2xdx=2⋅x22=x2
Evaluating from 0 to 2:
(x2)20=22−02=4−0=4
The second integral is:
∫3x2dx=3⋅x33=x3
Evaluating from 0 to 2:
(x3)20=23−03=8−0=8
Now we can combine the results of both integrals to find the total work done:
W=4+8=12J
The work done by the force as the particle moves from x=0 to x=2m is:
12J
Similar Questions
A force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=+2a. Where, k is a positive constant.
View SolutionA force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=2a. Here, k is a positive constant.
View Solution
Knowledge Check
- Question 1 - Select One
A force F is related to the position of a particle by the relation F=(10x2)N . Find the work done by the force when the particle moves from x=2m→x=4m.
A563 JB560 JC5603 JD3560 J
A force f=10+2x acts on a particle moving in straight line on x axis the work done by this force during a displacement from x=0 and x=3m
View SolutionForce acting on a particle varies with displacement as shown is Fig. Find the work done by this force on the particle from x=−4m to x = + 4m.
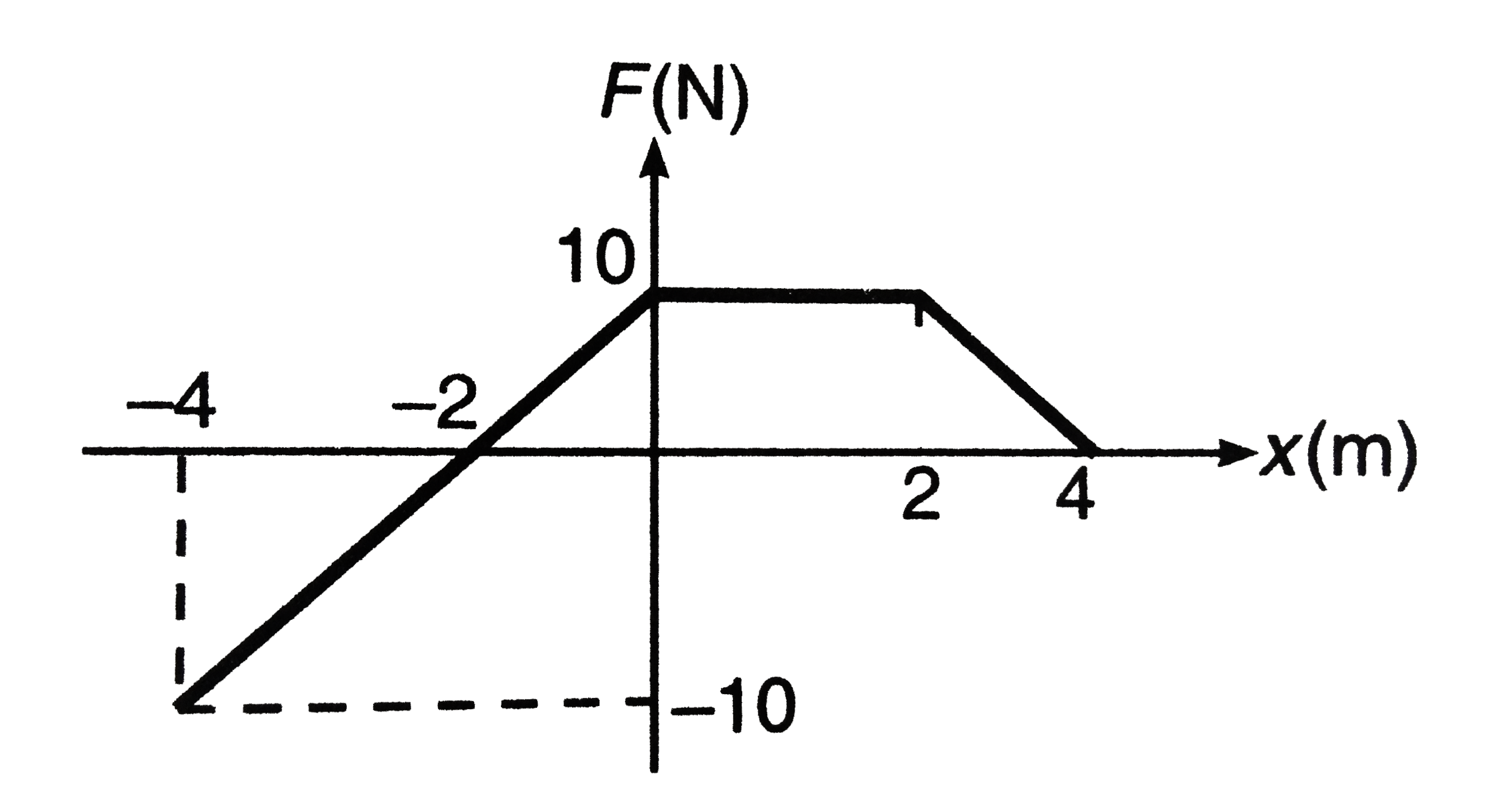 . View Solution
. View SolutionForce on a particle varies with position (x) of particle as shown, calculate work done by force from x=0 to x=30 m.
 View Solution
View SolutionA block is constrained to move along x-axis under a forc F=4x2(x≠0). Here, F is in newton and x in metre. Find the work done by this force when the block is displaced from x=4 m to x=2m.
View SolutionA force F=(5+2x) acts on a particle in x direction where F is in newtown and x is meter. Find the work done by this force during displacement from x=0 to x=1m.
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from
 View Solution
View SolutionA force F=(5+2x) acts on a particle in x direction where F is in Newtown and x is in meter. Find the work done by this force during displacement from x=0 to x=1m.
View Solution

