A hydrogen balloon is flying eastward with speed , when wind starts blowing from north to south with speed what is the resultant velocity of balloon ?
To find the resultant velocity of the hydrogen balloon flying eastward while the wind blows from north to south, we can follow these steps:
Step 1: Identify the velocities
- The velocity of the balloon flying eastward is Vb=12m/s (in the positive x-direction).
- The wind is blowing from north to south with a speed of Vw=5m/s (in the negative y-direction).
Step 2: Represent the velocities as vectors
- We can represent the velocity of the balloon as a vector:
→Vb=12^i+0^j
- The wind's velocity can be represented as:
→Vw=0^i−5^j
Step 3: Calculate the resultant velocity vector
- The resultant velocity →Vr of the balloon with respect to the ground can be found by adding the two vectors:
→Vr=→Vb+→Vw=(12^i+0^j)+(0^i−5^j)=12^i−5^j
Step 4: Calculate the magnitude of the resultant velocity
- The magnitude of the resultant velocity vector can be calculated using the Pythagorean theorem:
|→Vr|=√(12)2+(−5)2=√144+25=√169=13m/s
Step 5: Determine the direction of the resultant velocity
- The direction can be found using the tangent function:
tan(θ)=oppositeadjacent=−512
- This angle can be calculated using the arctangent function:
θ=tan−1(−512)
Final Result
- The resultant velocity of the balloon is 13m/s at an angle θ south of east.
- The velocity of the balloon flying eastward is Vb=12m/s (in the positive x-direction).
- The wind is blowing from north to south with a speed of Vw=5m/s (in the negative y-direction).
- We can represent the velocity of the balloon as a vector:
→Vb=12^i+0^j
- The wind's velocity can be represented as:
→Vw=0^i−5^j
- The resultant velocity →Vr of the balloon with respect to the ground can be found by adding the two vectors:
→Vr=→Vb+→Vw=(12^i+0^j)+(0^i−5^j)=12^i−5^j
- The magnitude of the resultant velocity vector can be calculated using the Pythagorean theorem:
|→Vr|=√(12)2+(−5)2=√144+25=√169=13m/s
- The direction can be found using the tangent function:
tan(θ)=oppositeadjacent=−512
- This angle can be calculated using the arctangent function:
θ=tan−1(−512)
- The resultant velocity of the balloon is 13m/s at an angle θ south of east.
Similar Questions
The S.I. unit of speed is ms−1
View SolutionA car is moving towards south with a speed of 20ms−1. A motorcycst is moving towards east with a speed of 15ms−1. At a crttain instant, the motorcyclistis due south of the car and is at a distance of 50mfrom the car.
The shortest distance between the motorcyclist and the car is.View Solution
Knowledge Check
- Question 1 - Select One
A river is flowing due east with a speed 3ms−1. A swimmer can swim in still water at a speed of 4ms−1. If swimmer starts swimming due north, then the resultant velocity of the swimmer is a) 3 m/s b) 5 m/s c) 7 m/s d) 2 m/s
A3 m s−1B5 m s−1C7 m s−1D2 m s−1 - Question 2 - Select One
A train approaching a railway platform with a speed of 20 m s−1 starts blowing the whistle. Speed of sound in air is 340 ms−1. If the frequency of the emitted sound from the whistle is 640 Hz, the frequency of sound as heard by person standing on the platform
A600 HzB640 HzC680 HzD720 Hz
A river is flowing due east with a speed 3ms−1 A swimmer can swim in still water at a speed of 4ms−1 If swimmer starts swimming due north what will be his resultant velocity (magnitude and direction )?
View SolutionA bird is fying due east with a velocity of 4ms−1. The starts to blow with a velocity of 3ms−1 due north. What is the magnituide of relative velocity of bird w.r.t. wind ? Find out its direction also.
View SolutionRain is falling vertically with a speed of 30 m/s. wind starts blowing after some time with a speed of 15 m/s in east to west direction. In which direction should a boy waiting at a bus hold his umbrella ?
View SolutionA balloon is moving along with constant upward acceleration of 1m/s2. A stone is thrown from the balloon downwards with speed 10m/s with respect to the balloon. At the time of projectile balloon is at height 120m from the ground and is moving with speed 20m/s. Find the time required to fall on the ground by the stone after the projection.
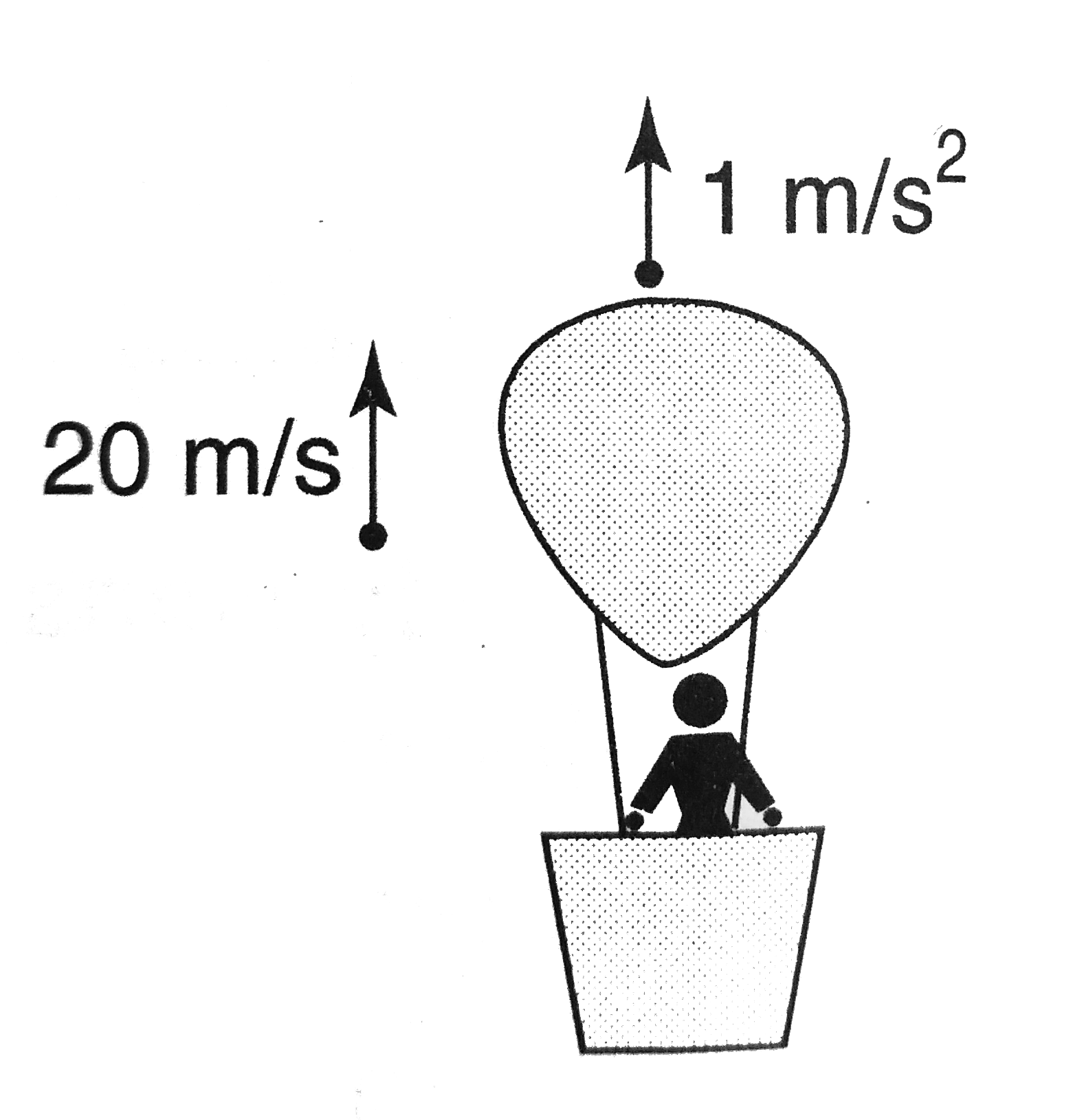 View Solution
View SolutionThe wind is blowing from south at 10 ms−1, but to a cyclist it appears blowing from the east at 10 ms−1. The velocity of cyclist is
View SolutionA ship is steaming towards east with a speed of 8 m/s. A women runs across the deck at a speed of 6ms−1 towards north. What is the velocity of the women relative to the sea ?
View Solution

