Frequency of a wave is 6×1015 Hz. The wave is
105cm−1
2×107m−1
2×107cm−1
2×105m−1
The correct Answer is:B
To determine the nature of the wave with a frequency of 6×1015 Hz, we can follow these steps:
Step 1: Understand the relationship between frequency, wavelength, and the speed of light.
The relationship between frequency (ν), wavelength (λ), and the speed of light (c) is given by the equation:
ν=cλ
where:
- ν is the frequency in hertz (Hz),
- c is the speed of light in vacuum, approximately 3×108 meters per second,
- λ is the wavelength in meters.
Step 2: Rearrange the formula to find the wavelength.
From the equation, we can rearrange it to find the wavelength:
λ=cν
Step 3: Substitute the known values into the equation.
Substituting the values of c and ν:
λ=3×108 m/s6×1015 Hz
Step 4: Calculate the wavelength.
Now, we perform the calculation:
λ=3×1086×1015=36×108−15=0.5×10−7 m=5×10−8 m
Step 5: Determine the type of wave.
The wavelength 5×10−8 meters (or 50 nm) falls within the electromagnetic spectrum, specifically in the ultraviolet (UV) range. Waves in this range are often associated with high energy and are capable of causing ionization.
Conclusion:
Thus, the wave with a frequency of 6×1015 Hz is an ultraviolet wave.
---
The relationship between frequency (ν), wavelength (λ), and the speed of light (c) is given by the equation:
ν=cλ
where:
- ν is the frequency in hertz (Hz),
- c is the speed of light in vacuum, approximately 3×108 meters per second,
- λ is the wavelength in meters.
From the equation, we can rearrange it to find the wavelength:
λ=cν
Substituting the values of c and ν:
λ=3×108 m/s6×1015 Hz
Now, we perform the calculation:
λ=3×1086×1015=36×108−15=0.5×10−7 m=5×10−8 m
The wavelength 5×10−8 meters (or 50 nm) falls within the electromagnetic spectrum, specifically in the ultraviolet (UV) range. Waves in this range are often associated with high energy and are capable of causing ionization.
Thus, the wave with a frequency of 6×1015 Hz is an ultraviolet wave.
Topper's Solved these Questions
- STRUCTURE OF ATOMBook:AAKASH INSTITUTE ENGLISHChapter:STRUCTURE OF ATOMExercise:ASSIGNMENT (SECTION -B) Objective type questions
Explore 34 Videos
- STRUCTURE OF ATOMBook:AAKASH INSTITUTE ENGLISHChapter:STRUCTURE OF ATOMExercise:ASSIGNMENT (SECTION -C) Previous Years Questions
Explore 47 Videos
- STRUCTURE OF ATOMBook:AAKASH INSTITUTE ENGLISHChapter:STRUCTURE OF ATOMExercise:EXERCISE
Explore 40 Videos
- STATES OF MATTERBook:AAKASH INSTITUTE ENGLISHChapter:STATES OF MATTERExercise:ASSIGNMENT (SECTION-D)
Explore 14 Videos
- STRUCTURE OF ATOM Book:AAKASH INSTITUTE ENGLISHChapter:STRUCTURE OF ATOM Exercise:ASSIGNMENT ( SECTION -J) Aakash Challengers Questions
Explore 12 Videos
Similar Questions
In an electromagnetic wave, the amplitude of electric field is 1V/m. The frequency of wave is 5×1014Hz. The wave is propagating along z-axis. The average energy density of electric field, in joule/m3,will be
View SolutionA plane light wave in the visible region is moving along the Z-direction. The frequency of the wave is0.5×1015 Hz and the electric field at any point is varying sinusoidally with time with an amplitude of 1V/m. Calculate the energy densities of the electric and magnetic fields.
View Solution
Knowledge Check
A light wave, travelling at 3×108m/s has a frequency of 6×1015 Hz. What is its wavelength?
A5×10−8mB2×10−7mC5×10−7mD5×10−6mFigure given shows a sinusoidal wave on a string. If the frequency of the wave is 150 Hz, what is the velocity and wavelength of the given wave?
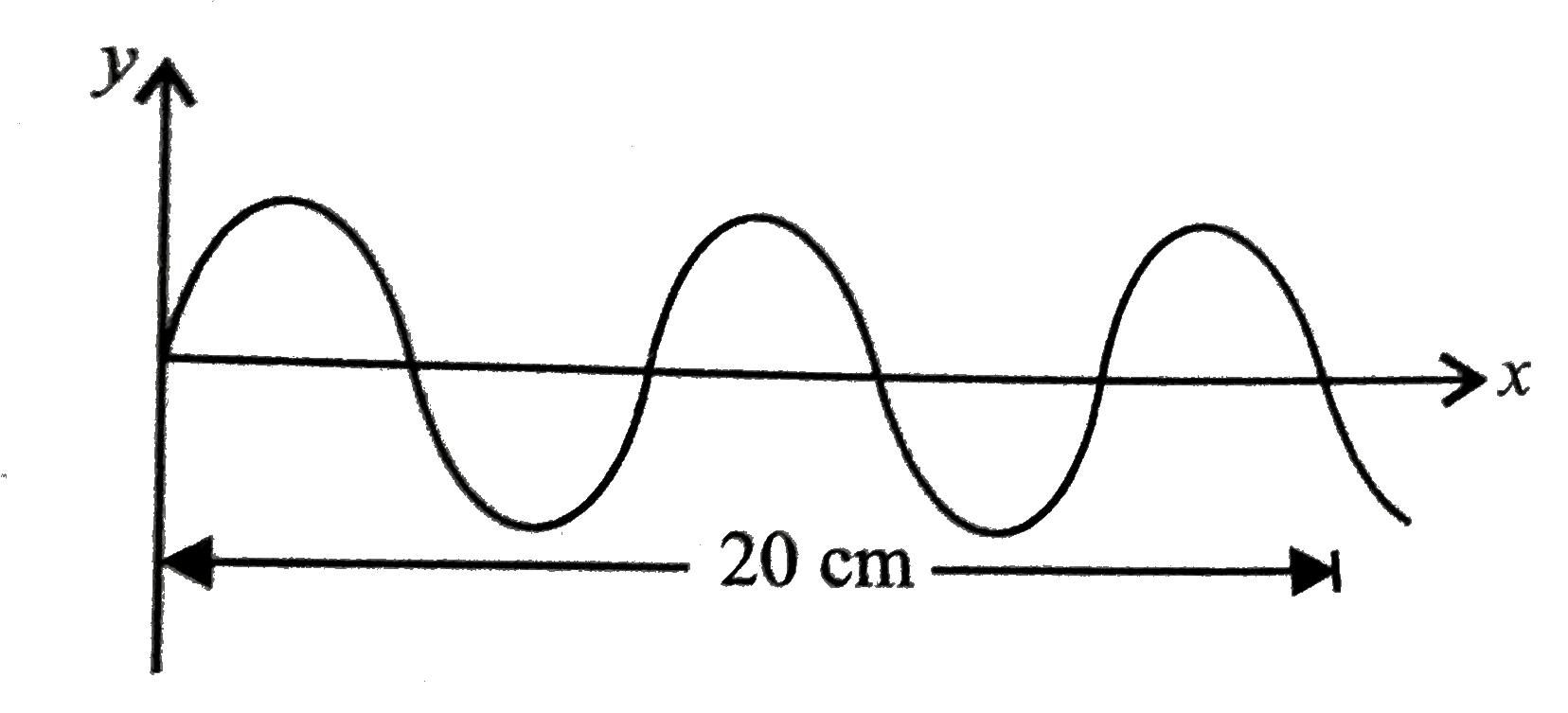 A0.04m,10ms−1B0.06m,12ms−1C0.08m,10ms−1D0.08m,12ms−1
A0.04m,10ms−1B0.06m,12ms−1C0.08m,10ms−1D0.08m,12ms−1
In an orbit of radius 0.5A0 an electron revolves with a frequency of 6.25×1015 Hz. The magnetic induction field at its centre is
View SolutionThe frequency of a radiation belonging to radio waves is 3×107Hz. Find the wave number and wavelength of the radiation.
View SolutionA wave has a frequency of 3×1015sec−1. The energy of that photon is
View SolutionAn EMW is travelling along z-axis →B=5×10−8ˆjT, C=3×108ms & Frequency of wave is 25 Hz, then electric field in volt/m.
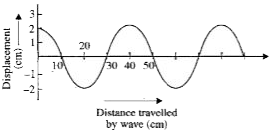
View SolutionA wave travelling along the length of a string is shown in Fig. 14.4.12. Using the scale on the given axis, find
(i) The amplitude of the wave
(ii) The wavelength of the wave
(iii) If the frequency of the wave is 10 Hz, What is the speed of the wave?
(iv) What is the initial phase of the wave ?
(v) What is the phase difference between two points separated by a distance 10 cm ?
(vi) If this wave is made to travel through water what is the wavelength of the wave, if the speed of, the waves in water is 10 m/s.
View SolutionThe frequency of plane progressive wave is 100 Hz. After how much time the same point will be 90∘ out of phase ?
View Solution
