An ideal gas is allowed to expand from 5 L to 15 L once rapidly and once very slowly. The magnitude of work done in two processes are W1 and W2, they are related as
W1=W2
W1>W2
W1<W2
Data is insufficient
The correct Answer is:C
To solve the problem, we need to analyze the work done during the expansion of an ideal gas in two different scenarios: one rapid and one slow.
1. Understanding Work Done in Gas Expansion:
The work done (W) by an ideal gas during expansion can be expressed mathematically as:
W=∫PdV
where P is the pressure and dV is the change in volume.
2. Rapid Expansion (W1):
In the case of rapid expansion, the gas expands quickly, and the pressure drops significantly during the process. This can be approximated as an irreversible expansion where the pressure remains constant until the gas reaches the new volume. However, since the expansion is rapid, the work done can be approximated as:
W1=Pinitial×(Vfinal−Vinitial)
where Vinitial=5L and Vfinal=15L.
3. Slow Expansion (W2):
In the case of slow expansion, the gas expands gradually, allowing the system to remain in equilibrium. The pressure changes continuously, and the work done can be calculated as:
W2=∫VfinalVinitialPdV
In this case, the work done is greater than in the rapid expansion because the pressure is higher at the initial volume and decreases gradually to the final volume.
4. Comparison of Work Done:
Since the work done in the slow process (W2) involves a gradual change in pressure, the area under the pressure-volume curve will be larger than in the rapid process (W1). Therefore, we can conclude:
W2>W1
5. Final Relationship:
The relationship between the work done in the two processes is:
W2>W1
Conclusion:
The magnitude of work done in the two processes is related as W2>W1.
---
The work done (W) by an ideal gas during expansion can be expressed mathematically as:
W=∫PdV
where P is the pressure and dV is the change in volume.
In the case of rapid expansion, the gas expands quickly, and the pressure drops significantly during the process. This can be approximated as an irreversible expansion where the pressure remains constant until the gas reaches the new volume. However, since the expansion is rapid, the work done can be approximated as:
W1=Pinitial×(Vfinal−Vinitial)
where Vinitial=5L and Vfinal=15L.
In the case of slow expansion, the gas expands gradually, allowing the system to remain in equilibrium. The pressure changes continuously, and the work done can be calculated as:
W2=∫VfinalVinitialPdV
In this case, the work done is greater than in the rapid expansion because the pressure is higher at the initial volume and decreases gradually to the final volume.
Since the work done in the slow process (W2) involves a gradual change in pressure, the area under the pressure-volume curve will be larger than in the rapid process (W1). Therefore, we can conclude:
W2>W1
The relationship between the work done in the two processes is:
W2>W1
The magnitude of work done in the two processes is related as W2>W1.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (Section - A) Objective Type Questions
55 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (Section - B) Objective Type Questions
35 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - SECTION-J
7 Videos
- THE SOLID STATE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THE SOLID STATE EXERCISE - Assignment (SECTION - D) (ASSERTION-REASON TYPE QUESTION)
20 Videos
Similar Questions
An ideal gas is allowed to expand against a constant pressure of 2 bar from 10L to 50 L in one step. Calculate the amount of work done by the gas. If the same expansion were carried out reversibly, will the work done be higher or lower than the earlier case ?
(Give that, 1 L bar = 100 J)
View SolutionAn ideal gas is allowed to expand from 1L to 10 L against a constant external pressure of 1 bar. The work done in x×10yJ. The numerical value of x is_____.
View Solution
Knowledge Check
A gas expands from i to f along the three paths indicated. The work done along the three paths denoted by W1,W2andW3 have the relationship
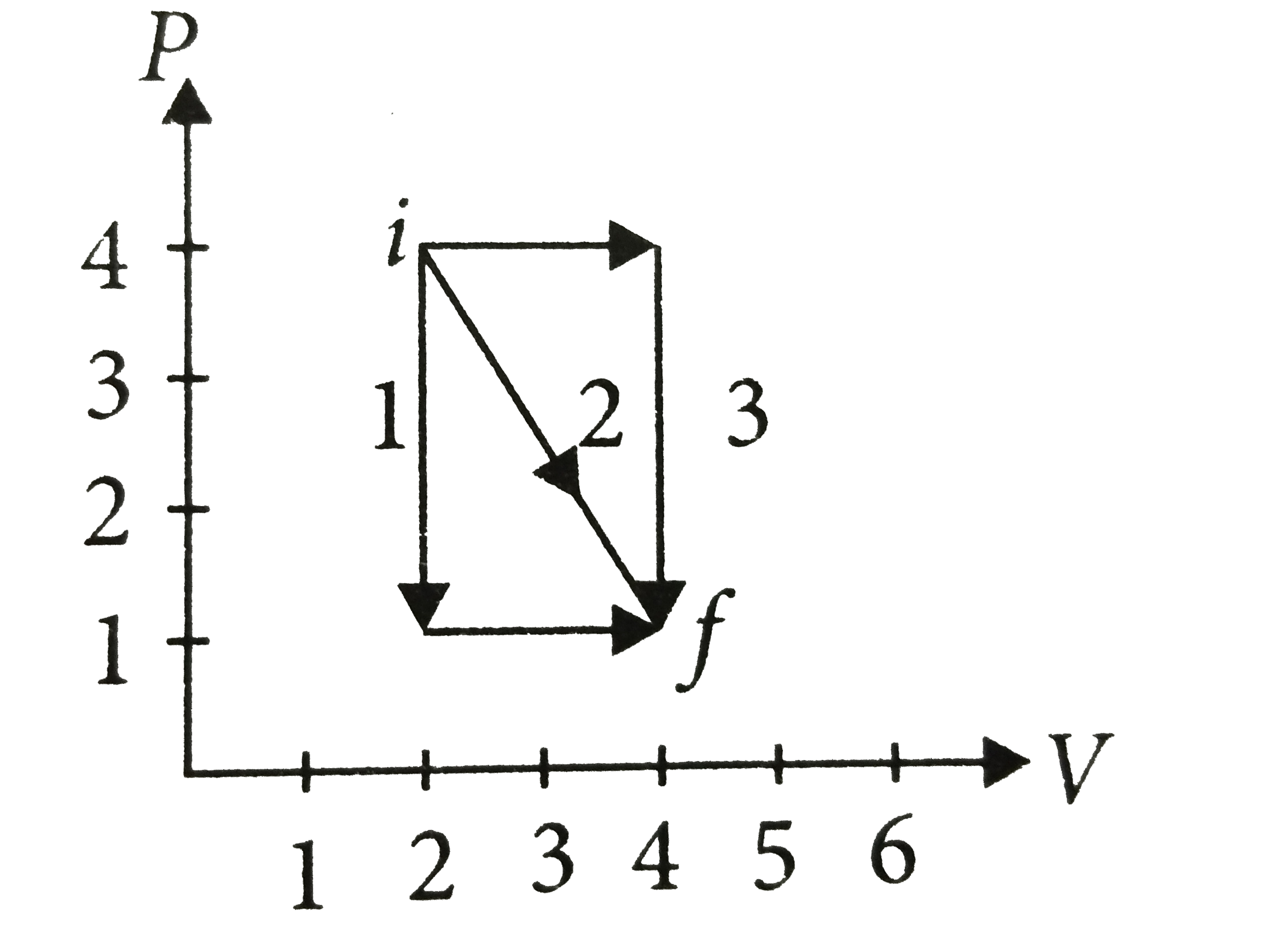 AW1<W2<W3BW2<W1=W3CW2<W1<W3DW1>W2>W3
AW1<W2<W3BW2<W1=W3CW2<W1<W3DW1>W2>W3Starting from the same initial conditions, an ideal gas expands from volume V1→V2 in three different ways. The work done by the gas is W1 if he process is purely isothermal, W2 if purely isobaric and W3 if purely adiabatic. Then
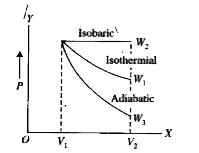 AW2>W1>W3BW2>W3>W1CW1>W2>W3DW1>W3>W2
AW2>W1>W3BW2>W3>W1CW1>W2>W3DW1>W3>W2
One mole of an ideal gas is allowed to expand reversible and adiabatically from a temperatureof27∘C)if the work done during the process is3kJ,the final temperature will be equal to(Cv=20JK−1)
View SolutionOne mole of an ideal gas is expanded from a volume of 3L to 5L under a constant pressure of 1 atm. Calculate the work done by the gas.
View Solution5mol of an ideal gas at 27∘C expands isothermally and reversibly from a volume of 6L to 60L. The work done in kJ is
View Solution5mol of an ideal gas at 27∘C expands isothermally and reversibly from a volume of 6L to 60L. The work done in kJ is
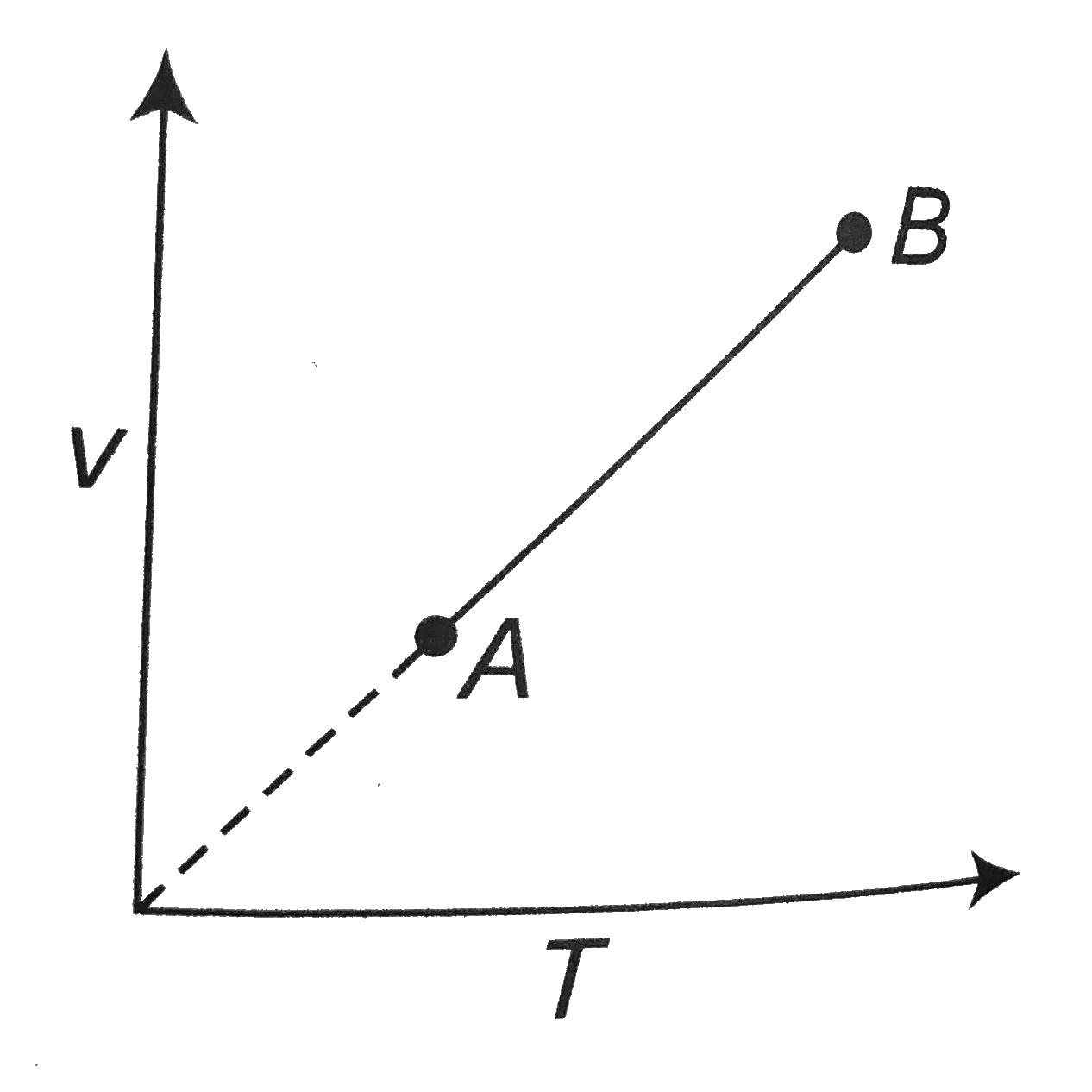
View SolutionAn ideal monoatomic gas undergoes the process AB as shown in the figure. If the heat supplied and the work done in the process are ΔQ and Delta Wrespectively.TheratioDeltaQ : DeltaW is
View Solution2 mol of an ideal gas at 27∘C expand isothermally and reversibly
from a volume of 2L to 20L. The work done (in KJ) by the gas is :-
View Solution
