For the reaction
aA(s)+bB(g)→dD(s)+cC(g). Then
ΔH−ΔE=(b−d)RT
ΔH−ΔE=(c−b)RT
ΔH−ΔE=(a+b)−(c+d)RT
ΔH−ΔE=(a−d)RT
The correct Answer is:B
To solve the problem, we need to find the relationship between the change in enthalpy (ΔH) and the change in internal energy (ΔE) for the given reaction:
aA(s)+bB(g)→dD(s)+cC(g)
1. Identify the Reaction Components:
- We have solid A and D, and gases B and C in the reaction.
- The stoichiometric coefficients are a, b, c, and d.
2. Write the Relationship Between ΔH and ΔE:
- The relationship between the change in enthalpy (ΔH) and the change in internal energy (ΔE) is given by the equation:
ΔH=ΔE+ΔNGRT
where ΔNG is the change in the number of moles of gas.
3. Calculate ΔN_G:
- To find ΔNG, we need to determine the change in the number of moles of gaseous products minus the change in the number of moles of gaseous reactants.
- From the reaction:
- Gaseous products: c moles of C
- Gaseous reactants: b moles of B
- Thus, we can calculate ΔNG as:
ΔNG=(moles of gaseous products)−(moles of gaseous reactants)=c−b
4. Substitute ΔN_G into the ΔH and ΔE Relationship:
- Now, substituting ΔNG back into the equation:
ΔH−ΔE=ΔNGRT
- Replacing ΔNG with c−b:
ΔH−ΔE=(c−b)RT
5. Final Result:
- Therefore, the relationship between ΔH and ΔE for the given reaction is:
ΔH−ΔE=(c−b)RT
- We have solid A and D, and gases B and C in the reaction.
- The stoichiometric coefficients are a, b, c, and d.
- The relationship between the change in enthalpy (ΔH) and the change in internal energy (ΔE) is given by the equation:
ΔH=ΔE+ΔNGRT
where ΔNG is the change in the number of moles of gas.
- To find ΔNG, we need to determine the change in the number of moles of gaseous products minus the change in the number of moles of gaseous reactants.
- From the reaction:
- Gaseous products: c moles of C
- Gaseous reactants: b moles of B
- Thus, we can calculate ΔNG as:
ΔNG=(moles of gaseous products)−(moles of gaseous reactants)=c−b
- Now, substituting ΔNG back into the equation:
ΔH−ΔE=ΔNGRT
- Replacing ΔNG with c−b:
ΔH−ΔE=(c−b)RT
- Therefore, the relationship between ΔH and ΔE for the given reaction is:
ΔH−ΔE=(c−b)RT
Topper's Solved these Questions
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (Section - B) Objective Type Questions
35 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (Section - C) Previous Years Questions
60 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercise
50 Videos
- THE SOLID STATE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THE SOLID STATE EXERCISE - Assignment (SECTION - D) (ASSERTION-REASON TYPE QUESTION)
20 Videos
Similar Questions
For the reaction PCl5(g)→PCl3(g)+Cl2(g)
View SolutionFor the reaction 18S8(s)+32O2(g)→SO3(g), the difference of heat change at constant pressure and constant volume at 27∘C will be.
View SolutionFor the reaction
N2(g)+3H2→2NH3(g)
ΔH=−85.4kJandΔS=−188.3Jk−1
Calculate the temperature at which Gibs energy change(ΔG) is equal to zero. Predict the nature of the reaction at this temperature and above it.
View SolutionFor the reaction
PCI3(g)+CI2(g)→PCI5(g),ΔH=−xkJ
If the ΔH∘fPCI3is−ykJ, what is ΔH∘fPCI5 ?
View SolutionFor the reaction, A(s)+3B(g)→4C(g)+d(l)ΔHandΔU are related as :
View SolutionFor the reversible reaction.
A(s)+B(g)⇔C(g)+D(g),△G∘=−350kJ
Which one of the following statement is true?
View SolutionA schematic representation of enthalpy changes for the reaction,Cgraphite+12O2(g)→CO(g) is given below. The missing value is
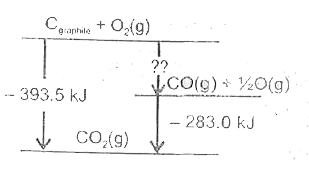
View SolutionFor the reaction
C3H8(g)+5O2(g)→3CO2(g)+4H2O(l) at constant temperature , ΔH−ΔE is
View SolutionFor the given reaction.
2A(s)+B(g)⇔C(g)+2D(s)+E(s)
the degree of dissociation of B was found to be 20% at 300k and 24% at 500 k the rate of backward reaction
View SolutionThe ΔS for the reaction
2H2(g)+O2(g)→2H2O(I)at500K when
S∘H2(g)=126.6,SO∘2(g)=201.20,
SH2O(I)=68.0JK−1mol−1 respectively is
View Solution