A solid with formula ABC3 would probably have
A at body centre, B at face centres and C at corners of the cube
A at corners of cube, B at body centre C at face centre
A at corners of hexagon, B at centres of the hexagon and C inside the hexagonal unit cell
A at corner, B at face centre, C at body centre
The correct Answer is:B
To determine the probable arrangement of atoms in a solid with the formula ABC3, we need to analyze the positions of the atoms A, B, and C based on the given options. Here’s a step-by-step breakdown of the solution:
Step 1: Analyze the given formula
The formula ABC3 indicates that:
- There is 1 atom of A
- There is 1 atom of B
- There are 3 atoms of C
Step 2: Evaluate the first option
The first option states:
- A is at the body center
- B is at the face centers
Calculating contributions:
- A (body center): There is 1 body center atom contributing 1 atom of A.
- B (face centers): There are 6 face centers, and each contributes 12. Thus, total contribution from B = 6×12=3.
Total atoms from this option:
- A = 1
- B = 3
- C = 0 (not mentioned)
This does not match the formula ABC3. Hence, this option is incorrect.
Step 3: Evaluate the second option
The second option states:
- A is at the corners
- B is at the body center
- C is at the face centers
Calculating contributions:
- A (corners): There are 8 corner atoms, each contributing 18. Thus, total contribution from A = 8×18=1.
- B (body center): There is 1 body center atom contributing 1 atom of B.
- C (face centers): There are 6 face centers, and each contributes 12. Thus, total contribution from C = 6×12=3.
Total atoms from this option:
- A = 1
- B = 1
- C = 3
This matches the formula ABC3. Hence, this option is correct.
Conclusion
The correct arrangement for the solid with the formula ABC3 is:
- A at corners
- B at body center
- C at face centers
The formula ABC3 indicates that:
- There is 1 atom of A
- There is 1 atom of B
- There are 3 atoms of C
The first option states:
- A is at the body center
- B is at the face centers
- A (body center): There is 1 body center atom contributing 1 atom of A.
- B (face centers): There are 6 face centers, and each contributes 12. Thus, total contribution from B = 6×12=3.
- A = 1
- B = 3
- C = 0 (not mentioned)
The second option states:
- A is at the corners
- B is at the body center
- C is at the face centers
- A (corners): There are 8 corner atoms, each contributing 18. Thus, total contribution from A = 8×18=1.
- B (body center): There is 1 body center atom contributing 1 atom of B.
- C (face centers): There are 6 face centers, and each contributes 12. Thus, total contribution from C = 6×12=3.
- A = 1
- B = 1
- C = 3
The correct arrangement for the solid with the formula ABC3 is:
- A at corners
- B at body center
- C at face centers
Topper's Solved these Questions
- THE SOLID STATE Book:AAKASH INSTITUTE ENGLISHChapter:THE SOLID STATE Exercise:Assignment (SECTION - B) (OBJECTIVE TYPE QUESTION)
Explore 25 Videos
- THE SOLID STATE Book:AAKASH INSTITUTE ENGLISHChapter:THE SOLID STATE Exercise:Assignment (SECTION - C) (PREVIOUS YEARS QUESTION)
Explore 41 Videos
- THE SOLID STATE Book:AAKASH INSTITUTE ENGLISHChapter:THE SOLID STATE Exercise:EXERCISE
Explore 30 Videos
- THE S-BLOCK ELEMENTSBook:AAKASH INSTITUTE ENGLISHChapter:THE S-BLOCK ELEMENTSExercise:Assignment (Section-J)
Explore 10 Videos
- THERMODYNAMICSBook:AAKASH INSTITUTE ENGLISHChapter:THERMODYNAMICSExercise:ASSIGNMENT (Section -D) Assertion-Reason Type Questions
Explore 15 Videos
Similar Questions
In period 2, element 'A' is to the right of element 'B'.
The element 'A' would probably have a ____ [smaller/larger] atomic size than 'B'.
View SolutionIn period 2, element 'A' is to the right of element 'B'.
The element 'B' would probably have ____[lower/higher] ionisation potential than 'A'.
View SolutionElement X forms a chloride with the formula XCl2, which is a solid with a high melting point. X would most likely be in the same group of the Periodic Table as
View SolutionIn the pedigree shown below, individuals with the solid symbols suffers from albinism. You would counsel the couple A & B that the probability that each of their child will have the disease is :-
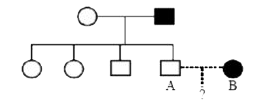
View SolutionA DNA with unequal nitrogen bases would most probably be
View SolutionWhat would be the formula of the compound formed by A and B, where A has the valence 3 and B has the valence 3 ?
View SolutionThe phosphate of a metal has the formula MHPO4. The formula of its chloride would be
View SolutionThe phosphate of a metal has the formula MHPO4. The formula of its chloride would be :
View SolutionA solid sphere and a solid hemi-sphere have the same total surface area. Find the ratio between their volumes.
View SolutionAmorphous solids have
View Solution