1 m aq. Solution of a salt shows elevation in boiling point equal to 3 times of its Kb. Determine
(i) Freezing point of solution
(ii) Osmotic pressure at 27∘C
To solve the problem step by step, we will determine the freezing point of the solution and the osmotic pressure at 27°C.
Given Data:
- Molality (M) = 1 molar
- Elevation in boiling point (ΔT_b) = 3 * K_b
- Van't Hoff factor (i) = 3 (as derived from the boiling point elevation)
Step 1: Calculate the Freezing Point of the Solution
Formula:
The depression in freezing point (ΔT_f) can be calculated using the formula:
ΔTf=i⋅Kf⋅M
Where:
- Kf for water = 1.86 °C kg/mol (standard value)
- M = 1 molar
- i = 3
Calculation:
Substituting the values into the formula:
ΔTf=3⋅1.86⋅1
ΔTf=5.58°C
Since the normal freezing point of water is 0 °C, the freezing point of the solution (T_f) will be:
Tf=0−ΔTf
Tf=0−5.58
Tf=−5.58°C
Step 2: Calculate the Osmotic Pressure at 27°C
Formula:
The osmotic pressure (π) can be calculated using the formula:
π=i⋅C⋅R⋅T
Where:
- C = concentration (1 molar)
- R = universal gas constant = 0.0821 L·atm/(K·mol)
- T = temperature in Kelvin = 27°C + 273 = 300 K
- i = 3
Calculation:
Substituting the values into the formula:
π=3⋅1⋅0.0821⋅300
π=3⋅0.0821⋅300
π=73.89atm
Final Answers:
(i) Freezing point of the solution = -5.58 °C
(ii) Osmotic pressure at 27°C = 73.89 atm
- Molality (M) = 1 molar
- Elevation in boiling point (ΔT_b) = 3 * K_b
- Van't Hoff factor (i) = 3 (as derived from the boiling point elevation)
The depression in freezing point (ΔT_f) can be calculated using the formula:
ΔTf=i⋅Kf⋅M
- Kf for water = 1.86 °C kg/mol (standard value)
- M = 1 molar
- i = 3
Substituting the values into the formula:
ΔTf=3⋅1.86⋅1
ΔTf=5.58°C
Tf=0−ΔTf
Tf=0−5.58
Tf=−5.58°C
The osmotic pressure (π) can be calculated using the formula:
π=i⋅C⋅R⋅T
- C = concentration (1 molar)
- R = universal gas constant = 0.0821 L·atm/(K·mol)
- T = temperature in Kelvin = 27°C + 273 = 300 K
- i = 3
Substituting the values into the formula:
π=3⋅1⋅0.0821⋅300
π=3⋅0.0821⋅300
π=73.89atm
(i) Freezing point of the solution = -5.58 °C
(ii) Osmotic pressure at 27°C = 73.89 atm
Topper's Solved these Questions
- SOLUTIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SOLUTIONSEXERCISE - ASSIGMENT (SECTION-A)
50 Videos
- SOLUTIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SOLUTIONSEXERCISE - ASSIGMENT (SECTION-B)
21 Videos
- SOLUTIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SOLUTIONSEXERCISE - ASSIGMENT (SECTION-J) AAKASH CHALLENGERS QUESTIONS
10 Videos
- REDOX REACTIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - REDOX REACTIONSEXERCISE - ASSIGNMENT SECTION - D
10 Videos
- SOME BASIC CONCEPT OF CHEMISTRYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SOME BASIC CONCEPT OF CHEMISTRYEXERCISE - ASSIGNMENT( SECTION - D) Assertion-Reason Type Questions
15 Videos
Similar Questions
Knowledge Check
A solution of urea in water has a boiling point of 100.18∘C . Calculate the freezing point of the solution.
A−0.4539∘CB−0.6539∘CC−0.4859∘CD−0.5539∘C
If for a sucrose, elevation in boiling point is 1.0∘C, then what will be the boiling point of NaCl solution for same molal concentration?
View SolutionA 0.1 molal aqueous solution of a weak acid is 30% ionized. If Kf for water is 1.86∘C/m, the freezing point of the solution will be.
View SolutionEquimolal solutions A and B show depression in freezing point in the ratio 2:1. A remains in the normal state in solution. B will be
View SolutionThe boiling point of 0.1MKCl solution is ………..than 100∘C.
View SolutionAn aqueous solution freezes at −0.2∘C. What is the molality of the solution ?
Determine also (i) elevation in the boiling point
(ii) lowering in vapour pressure at 25∘C, given that Kf=1.86∘C kg mol−1,Kb=0.512∘C kg mol−1, and vapour pressure of water at 25∘C is 23.756 mm.
View SolutionConsider following figure and answer the questions at the end of it. Figure explains elevation in boiling point when a non-volatile solute is added to a solvent.
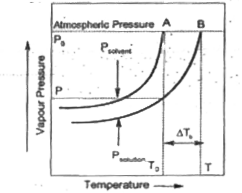
Variation of vapour pressure with temperature and showing elevation in boiling point.
Given that ΔTb is the elevation in boiling point of the solvent in a solution of molality m then Ltm→0(ΔTbm) is equal to
View SolutionConsider following figure and answer the questions at the end of it. Figure explains elevation in boiling point when a non-volatile solute is added to a solvent.
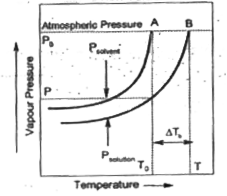
Variation of vapour pressure with temperature and showing elevation in boiling point.
Elevation in boiling point of an aqueous urea solution is 0.52∘.(Kb=0.52∘mol−1kg). Hence, mole fraction of urea in this solution is:
View Solution
