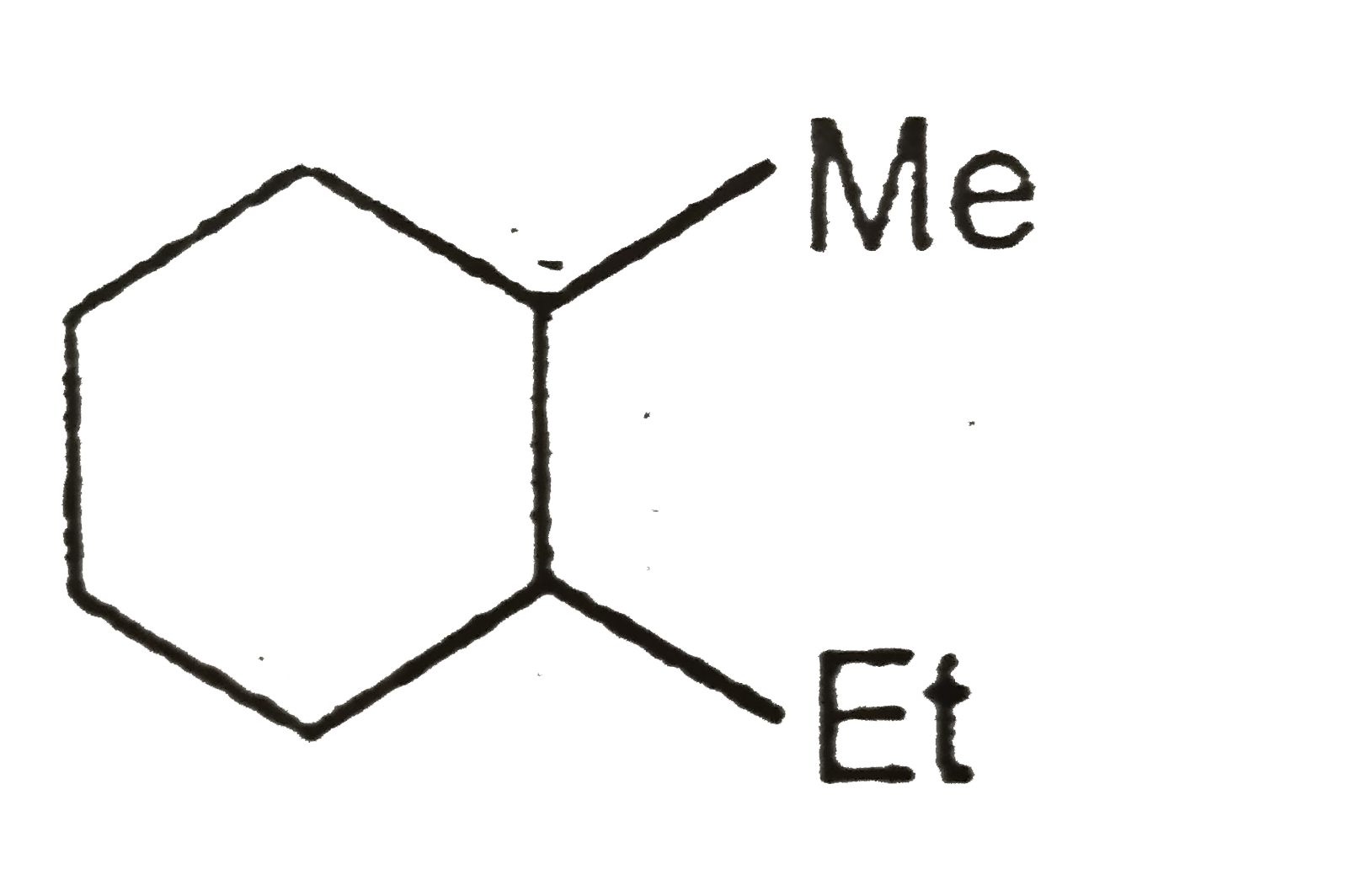
Number of geometrical isomers possible for[MABCDEF] are
6
10
15
12
The correct Answer is:C
To determine the number of geometrical isomers possible for the complex (MABCDEF), we can follow these steps:
Step 1: Identify the Geometry of the Complex
The complex (MABCDEF) has six ligands (A, B, C, D, E, F), which indicates that it adopts an octahedral geometry.
Hint: Remember that octahedral complexes can have different arrangements of ligands leading to geometrical isomers.
Step 2: Understand Geometrical Isomers
Geometrical isomers arise when ligands can occupy different positions relative to each other. In octahedral complexes, we typically consider cis and trans arrangements.
Hint: Geometrical isomers can be classified as cis (adjacent ligands) and trans (opposite ligands).
Step 3: Fix Two Ligands
To find the number of geometrical isomers, we can fix two ligands in specific positions. For example, we can fix ligands A and B at the top and bottom of the octahedron.
Hint: Fixing two ligands helps simplify the arrangement of the remaining ligands.
Step 4: Calculate the Combinations of Remaining Ligands
After fixing two ligands, we have four remaining ligands (C, D, E, F) that can be arranged in various ways. We can calculate the number of ways to choose 2 ligands from the 6 to fix their positions.
The formula for combinations is given by:
C(n,r)=n!r!(n−r)!
Where n is the total number of ligands and r is the number of ligands to choose.
Hint: Use the combination formula to determine how many pairs of ligands can be fixed.
Step 5: Apply the Combination Formula
For our case:
- Total ligands n=6
- Ligands to fix r=2
Calculating C(6,2):
C(6,2)=6!2!(6−2)!=6!2!⋅4!=6×5×4!2!×4!=302=15
Hint: Factorials can simplify the calculation significantly, especially when terms cancel out.
Step 6: Conclusion
Thus, the total number of geometrical isomers for the complex (MABCDEF) is 15.
Final Answer: The correct option is C: 15.
The complex (MABCDEF) has six ligands (A, B, C, D, E, F), which indicates that it adopts an octahedral geometry.
Geometrical isomers arise when ligands can occupy different positions relative to each other. In octahedral complexes, we typically consider cis and trans arrangements.
To find the number of geometrical isomers, we can fix two ligands in specific positions. For example, we can fix ligands A and B at the top and bottom of the octahedron.
After fixing two ligands, we have four remaining ligands (C, D, E, F) that can be arranged in various ways. We can calculate the number of ways to choose 2 ligands from the 6 to fix their positions.
C(n,r)=n!r!(n−r)!
Where n is the total number of ligands and r is the number of ligands to choose.
For our case:
- Total ligands n=6
- Ligands to fix r=2
C(6,2)=6!2!(6−2)!=6!2!⋅4!=6×5×4!2!×4!=302=15
Thus, the total number of geometrical isomers for the complex (MABCDEF) is 15.
Topper's Solved these Questions
- ALCOHOLS, PHENOLS AND ETHERSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALCOHOLS, PHENOLS AND ETHERSEXERCISE - Try yourself
5 Videos
- ALCOHOLS, PHENOLS AND ETHERSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALCOHOLS, PHENOLS AND ETHERSEXERCISE - Exercise
40 Videos
- ALCOHOLS, PHENOLS AND ETHERS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALCOHOLS, PHENOLS AND ETHERS EXERCISE - Try Yourself
5 Videos
Similar Questions
Knowledge Check
Geometrical isomers are possible for :
ACH3CH2−C∣∣NOH−CH2CH3BCH3CH2−C∣∣O−CH3CCH3CH2−C∣∣NOH−CH3DC6H5−C∣∣O−C6H5Geometrical isomerism is possible in :
A B
B C
C D
D
Geometrical isomerism is possible in :
A B
B C
C D
D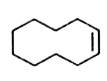
How many geometrical isomers are possible for

View SolutionGeometrical isomers differ in
View SolutionFind the number of geometrical isomers possible of the following compounds.

View SolutionThe number of geometric isomers possible for the complex [CoL2Cl2]−(L=H2NCH2CH2O−) is
View SolutionGeometrical isomers differ in:
View Solution