α−(D) glucose ⇔β−(D) glucose, equilibrium constant for this s 1.8. The percentage of α−(D) glucose at equilibrium is
35.7
55.6
44.4
64.3
The correct Answer is:A
To solve the problem of calculating the percentage of α-(D) glucose at equilibrium when it converts to β-(D) glucose with an equilibrium constant (K) of 1.8, we can follow these steps:
1. Define Initial Concentrations:
- Let the initial concentration of α-(D) glucose be 1 (1 mole).
- The initial concentration of β-(D) glucose is 0.
2. Define Change at Equilibrium:
- At equilibrium, let the concentration of α-(D) glucose be α.
- Therefore, the concentration of β-(D) glucose at equilibrium will be 1−α.
3. Write the Expression for Equilibrium Constant (K):
- The equilibrium constant K is given by the formula:
K=(α-(D) glucose)(β-(D) glucose)
- Substituting the equilibrium concentrations, we have:
K=α1−α
- Given that K=1.8, we can set up the equation:
α1−α=1.8
4. Solve for α:
- Cross-multiply to solve for α:
α=1.8(1−α)
α=1.8−1.8α
α+1.8α=1.8
2.8α=1.8
α=1.82.8≈0.642
5. Calculate the Concentration of β-(D) Glucose:
- The concentration of β-(D) glucose at equilibrium is:
1−α=1−0.642=0.358
6. Calculate the Percentage of α-(D) Glucose:
- The percentage of α-(D) glucose at equilibrium is given by:
Percentage of α-(D) glucose=α×100=0.642×100≈64.2%
7. Final Answer:
- The percentage of α-(D) glucose at equilibrium is approximately 64.2%.
- Let the initial concentration of α-(D) glucose be 1 (1 mole).
- The initial concentration of β-(D) glucose is 0.
- At equilibrium, let the concentration of α-(D) glucose be α.
- Therefore, the concentration of β-(D) glucose at equilibrium will be 1−α.
- The equilibrium constant K is given by the formula:
K=(α-(D) glucose)(β-(D) glucose)
- Substituting the equilibrium concentrations, we have:
K=α1−α
- Given that K=1.8, we can set up the equation:
α1−α=1.8
- Cross-multiply to solve for α:
α=1.8(1−α)
α=1.8−1.8α
α+1.8α=1.8
2.8α=1.8
α=1.82.8≈0.642
- The concentration of β-(D) glucose at equilibrium is:
1−α=1−0.642=0.358
- The percentage of α-(D) glucose at equilibrium is given by:
Percentage of α-(D) glucose=α×100=0.642×100≈64.2%
- The percentage of α-(D) glucose at equilibrium is approximately 64.2%.
Topper's Solved these Questions
- BIOMOLECULESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - BIOMOLECULESEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
5 Videos
- BIOMOLECULESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - BIOMOLECULESEXERCISE - EXERCISE (ASSIGNMENT) SECTION - C Previous Years Questions
25 Videos
- AMINES BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - AMINES EXERCISE - Assignment Section -J (Aakash Challengers Questions)
9 Videos
- CHEMICAL BONDING AND MOLECULAR STRUCTURE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CHEMICAL BONDING AND MOLECULAR STRUCTURE EXERCISE - Assignment Section J (Aakash Challengers Questions)
10 Videos
Similar Questions
Knowledge Check
α-D(+)-glucose and β-D(+) glucose are
AanomersBenantiomersCgeometrical isomersDepimersD (+) Glucose has melting point 146∘C and specific rotation [α]25D is + 112∘C. Another D(+) Glucose has melting point 150∘C and specific rotational [α]25Dis +18.7∘C. The two form have significantly different optical rotation but when an aqueous solution of either form is allowed to stand, it rotation changes. The specific rotation of one form decreases and rotation of other increases until both solution show the same value +52.7∘. The change in rotation towards an equilibrium value is called mutarotation.
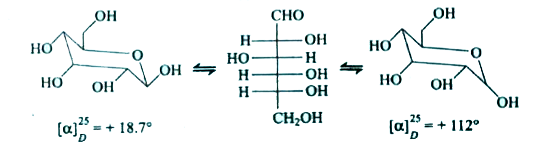
What percentage of β-D-(+) glucopyranose found at equilibrium in the aqueous solution?A50%B≈100%C38%D64%
Correct statement for α-D-glucose is
View SolutionDraw the structures of α-D-glucose and β-D-glucose
View Solutionα-D-Glucopyranose and β-D-Glucopyranose are
View SolutionWhich component of starch is a branched polymer of α−glucose and insoluble in water ?
View SolutionFollowing enthalpy changes are given:
α−Dglucose(s)→α−Dglucoes(aq),ΔH=10.72kJ
β−Dglucose(s)→β−Dglucose(aq),ΔH=4.68kJ
α−Dglucose(aq)→β−Dglucose(aq),ΔH=1.16kJ
Calculate enthalpy change in
α−Dglucose(s)→β−Dglucose(s)
View SolutionThe enthalpy changes of some process are given below
α−Dglucose(s)+H2O→α−D−glucose(aq) Heat of dissolution =10.84kJ
β−Dglucose(s)+H2O→β−D−glucose(aq) Heat of dissolution = 4.68kJ
α−Dglucose(aq)→β−D−glucose(aq) Heat of mutarotation =−1.16kJ
The ΔH0for α−Dglucose(s)→β−Dglucose(s) is
View Solution
