A parallel plate capacitor of capacitance C has been charged, so that the potential difference between its plates is V. Now, the plates of this capacitor are connected to another uncharged capacitor of capacitance 2C. Find the common potential acquired by the system and loss of energy.
To solve the problem of the parallel plate capacitor, we will follow these steps:
Step 1: Understand the initial conditions
The initial capacitance of the first capacitor is C and it is charged to a potential difference V. The initial charge Q on the capacitor can be calculated using the formula:
Q=C⋅V
Step 2: Connect the charged capacitor to the uncharged capacitor
When the charged capacitor is connected to an uncharged capacitor of capacitance 2C, the total capacitance of the system becomes:
Ctotal=C+2C=3C
Step 3: Calculate the common potential
The total charge in the system remains conserved. The total charge before connecting the capacitors is Q=C⋅V. After connecting the capacitors, the common potential Vf across both capacitors can be found using the formula:
Q=Ctotal⋅Vf
Substituting the values we have:
C⋅V=3C⋅Vf
Solving for Vf:
Vf=C⋅V3C=V3
Step 4: Calculate the loss of energy
The initial energy stored in the first capacitor is given by:
Ui=12CV2
The energy stored in the system after connecting the capacitors, with the common potential Vf, is:
Uf=12CV2f+12(2C)V2f=12C(V3)2+12(2C)(V3)2
Calculating Uf:
Uf=12C⋅V29+C⋅V29=12⋅V29C+22⋅V29C=32⋅V29C=V2C6
Step 5: Find the loss of energy
The loss of energy ΔU in the system is given by:
ΔU=Ui−Uf
Substituting the values:
ΔU=12CV2−V2C6
Finding a common denominator (which is 6):
ΔU=36CV2−16CV2=26CV2=13CV2
Final Answers
- The common potential acquired by the system is V3.
- The loss of energy is 13CV2.
The initial capacitance of the first capacitor is C and it is charged to a potential difference V. The initial charge Q on the capacitor can be calculated using the formula:
Q=C⋅V
When the charged capacitor is connected to an uncharged capacitor of capacitance 2C, the total capacitance of the system becomes:
Ctotal=C+2C=3C
The total charge in the system remains conserved. The total charge before connecting the capacitors is Q=C⋅V. After connecting the capacitors, the common potential Vf across both capacitors can be found using the formula:
Q=Ctotal⋅Vf
Substituting the values we have:
C⋅V=3C⋅Vf
Solving for Vf:
Vf=C⋅V3C=V3
The initial energy stored in the first capacitor is given by:
Ui=12CV2
The energy stored in the system after connecting the capacitors, with the common potential Vf, is:
Uf=12CV2f+12(2C)V2f=12C(V3)2+12(2C)(V3)2
Calculating Uf:
Uf=12C⋅V29+C⋅V29=12⋅V29C+22⋅V29C=32⋅V29C=V2C6
The loss of energy ΔU in the system is given by:
ΔU=Ui−Uf
Substituting the values:
ΔU=12CV2−V2C6
Finding a common denominator (which is 6):
ΔU=36CV2−16CV2=26CV2=13CV2
- The common potential acquired by the system is V3.
- The loss of energy is 13CV2.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXERCISE20videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - A44videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-J Aakash Challengers Questions5videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions25videos
ELECTROMAGNETIC WAVES
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)15videos
GRAVITATION
Similar Questions
In a parallel plate capacitor of capacitor 1μF two plates are given charges 2μC and 4μC the potential difference between the plates of the capacitor is
_2019_CBT2_E01_002_Q01.png) View Solution
View SolutionA capacitor of capacitance C is charged to a potential differece V0. The terminals of the charged capacitor are then connected to those of an uncharged capacitor of capacitance C/2.
a. Compute the original charge of the system.
b. Find the final potential differce across each capacitor.
c. Find the final energy of the system.
d. Calculate the decrease in energy when the capacitors are connected.
e. Where did the ''lost'' energy go?View SolutionTwo parallel conducting plates of a capacitor of capacitance C containing charges Q and -2Q at a distance d apart. Find out potential difference between the plates of capacitors.
View SolutionA parallel plate capacitor of capacitane C is charged to a potential V. It is then connected to another uncharged capacitor with the same capacitance. Find out the ratio of the energy stored in the combined system to that stored initially in the single capacitor.
View SolutionA parallel plate air capacitor has capcity C distance of separtion between plates is d and potential difference V is applied between the plates force of attraction between the plates of the parallel plate air capacitor is
View SolutionA capacitor of capacitance C is charged to a potential difference V0. The charged battery is disconnected and the capacitor is connected to a capacitor of unknown capacitance Cx. The potential difference across the combination is V. The value of Cx should be
View SolutionOne plate of a capacitor of capacitance 2μF has total charge +10μC and its other plate has total charge +40μC. The potential difference between the plates is (in Volt).
View SolutionA parallel plate capacitor of capacitance C (without dielectric) is filled by dielectric slabs as shown in figure. Then the new capacitance of the capacitor is
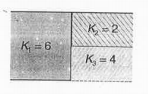 View Solution
View SolutionA capacitor of capacitance C1 is charged to a potential difference V and then connected with an uncharged capacitor of capacitance C2 a resistance R. The switch is closed at t = 0. Choose the correct option(s):
View SolutionA capacitor of capacity 20microF is charged upto 500V and and disconnected from cell. Now this charged capacitor is connected to another capacitor of capacitance C If final common potential is 20V then find the capacitance C.
View Solution

