An uncharged capacitor is fully charged with a battery . The ratio of energy stored in the capacitor to the work done by the battery in this process is
1:2
2:1
1:1
2:3
The correct Answer is:A
To solve the problem of finding the ratio of energy stored in a capacitor to the work done by the battery when charging the capacitor, we can follow these steps:
Step 1: Understand the basic concepts
- An uncharged capacitor is charged by a battery.
- The capacitance of the capacitor is denoted as C.
- The voltage of the battery is denoted as V.
Step 2: Calculate the charge on the capacitor
The charge Q stored in the capacitor when fully charged is given by the formula:
Q=C×V
Step 3: Calculate the energy stored in the capacitor
The energy U stored in the capacitor can be calculated using the formula:
U=Q22C
Substituting Q=C×V into the energy formula:
U=(C×V)22C=C2V22C=12CV2
Step 4: Calculate the work done by the battery
The work done W by the battery while charging the capacitor can be calculated as:
W=Q×V
Substituting Q=C×V:
W=(C×V)×V=CV2
Step 5: Find the ratio of energy stored to work done
Now, we need to find the ratio of the energy stored in the capacitor to the work done by the battery:
Ratio=UW=12CV2CV2
This simplifies to:
Ratio=12
Conclusion
Thus, the ratio of the energy stored in the capacitor to the work done by the battery is:
Ratio=12
- An uncharged capacitor is charged by a battery.
- The capacitance of the capacitor is denoted as C.
- The voltage of the battery is denoted as V.
The charge Q stored in the capacitor when fully charged is given by the formula:
Q=C×V
The energy U stored in the capacitor can be calculated using the formula:
U=Q22C
Substituting Q=C×V into the energy formula:
U=(C×V)22C=C2V22C=12CV2
The work done W by the battery while charging the capacitor can be calculated as:
W=Q×V
Substituting Q=C×V:
W=(C×V)×V=CV2
Now, we need to find the ratio of the energy stored in the capacitor to the work done by the battery:
Ratio=UW=12CV2CV2
This simplifies to:
Ratio=12
Thus, the ratio of the energy stored in the capacitor to the work done by the battery is:
Ratio=12
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - A
44 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - B
38 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXAMPLE
138 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
Similar Questions
A battery is used to charge a parallel plate capacitor till the potential differece between the plates becomes equal to the electromotive force of the battery. The ratio of the energy stored in the capacitor and the work done by the battery will be
View SolutionA 12 pF capacitor is connected to a 50 V battery. How much electrostatic energy is stored in the capacitor ?
View Solution
Knowledge Check
A capacitor of capacitance 700 pF is charged by 100 V battery. The electrostatic energy stored by the capacitor is
A2.5×10−8JB3.5×10−6JC2.5×10−4JD3.5×10−4J
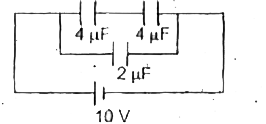
If initial charge on all the capacitors were zero , work done by the battery in the circuit shown is
View SolutionAssertion : When an uncharged capacitor is charged by a battery only 50% of the energy supplied is stored in the capacitor.
Reason : Rest 50% is lost.
View SolutionAnswer the following:
(a) Describe briefly the process of transferring charge between the two plates of a parallel plate capacitor when connected to a battery. Derive an expression for the energy stored in a capacitor.
(b) A parallel plate capacitor is connected to a battery of potential difference V. It is disconnected from battery and then connected to another uncharged capacitor of the same capacitance. Calculate the ratio of the energy stored in the combination to the initial energy on the single capacitor.
View SolutionA 900 pF capacitor is charged by 100V battery.
(a) How much electrostatic energy is strored by the capacitor ? The capacitor is disconnected from the battery and connected to another 900 pF capacitor. How much is the electrostatic energy stored in the system ?
View SolutionA parallel plate capacitor of capacitane C is charged to a potential V. It is then connected to another uncharged capacitor with the same capacitance. Find out the ratio of the energy stored in the combined system to that stored initially in the single capacitor.
View SolutionAn uncharged capacitor is connected to a battery. Show that half the energy supplied by the battery is lost as heat while charging the capacitor.
View SolutionA parallel plate capacitor of capacity C0 is charged to a potential V0,E1 is the energy stored in the capacitor when the battery is disconnected and the plate separation is doubled, and E2 is the energy stored in the capacitor when the charging battery is kept connected and the separation between the capacitor plates is dounled. find the ratio E1/E2.
View Solution
