considering the electron of outermost orbital of CU match the items given the column I with their values given in column II. Column-I { (A) orbital angular momentum, (B) angular momentum in an orbit, (C) spin angular momentum} Column - II ( I. 4h, II. 0, III. 0.86h, IV. 1.73)
A(II),B(I), C(III)
A(III),B(IV),C(II)
A(I),B(IV),C(II)
A(I),B(II),C(III)
The correct Answer is:A
To solve the problem of matching the items in Column I with their corresponding values in Column II for the outermost electron of copper (Cu), we will follow these steps:
Step 1: Determine the electronic configuration of copper
Copper (Cu) has an atomic number of 29. The electronic configuration is:
- 1s² 2s² 2p⁶ 3s² 3p⁶ 3d¹⁰ 4s¹
The outermost electrons are in the 4s and 3d orbitals.
Step 2: Identify the outermost orbital
The outermost orbital for the electron in copper is the 4s orbital, which contains one electron.
Step 3: Calculate the orbital angular momentum (L)
The formula for orbital angular momentum is given by:
L=l⋅ℏ
where l is the azimuthal quantum number. For the s orbital, l=0.
However, since we are considering the outermost orbital (4s), we need to calculate the total orbital angular momentum for the outermost electron:
- For the 4s orbital, l=0
- Therefore, the orbital angular momentum L=0⋅ℏ=0
Step 4: Calculate the total angular momentum in an orbit
The total angular momentum in an orbit is also determined by the quantum number l. Since the outermost electron is in the s orbital:
- L=0
Step 5: Calculate the spin angular momentum (S)
The formula for spin angular momentum is:
S=√s(s+1)⋅ℏ
where s is the spin quantum number. For an electron, s=12.
Calculating the spin angular momentum:
S=√12(12+1)⋅ℏ=√12⋅32⋅ℏ=√34⋅ℏ=√32⋅ℏ
Using the approximate value of √3≈1.73:
S≈0.86ℏ
Step 6: Match the values from Column I to Column II
Now we can match the calculated values with those in Column II:
- (A) Orbital angular momentum: 0 (matches with II)
- (B) Angular momentum in an orbit: 0 (matches with II)
- (C) Spin angular momentum: 0.86ℏ (matches with III)
Final Matching
- A matches with II (0)
- B matches with I (4h)
- C matches with III (0.86h)
Thus, the final matches are:
- A → II
- B → I
- C → III
Copper (Cu) has an atomic number of 29. The electronic configuration is:
- 1s² 2s² 2p⁶ 3s² 3p⁶ 3d¹⁰ 4s¹
The outermost orbital for the electron in copper is the 4s orbital, which contains one electron.
The formula for orbital angular momentum is given by:
L=l⋅ℏ
where l is the azimuthal quantum number. For the s orbital, l=0.
- For the 4s orbital, l=0
- Therefore, the orbital angular momentum L=0⋅ℏ=0
The total angular momentum in an orbit is also determined by the quantum number l. Since the outermost electron is in the s orbital:
- L=0
The formula for spin angular momentum is:
S=√s(s+1)⋅ℏ
where s is the spin quantum number. For an electron, s=12.
S=√12(12+1)⋅ℏ=√12⋅32⋅ℏ=√34⋅ℏ=√32⋅ℏ
S≈0.86ℏ
Now we can match the calculated values with those in Column II:
- (A) Orbital angular momentum: 0 (matches with II)
- (B) Angular momentum in an orbit: 0 (matches with II)
- (C) Spin angular momentum: 0.86ℏ (matches with III)
- A matches with II (0)
- B matches with I (4h)
- C matches with III (0.86h)
- A → II
- B → I
- C → III
Topper's Solved these Questions
Similar Questions
match the items given in column I with the items given in column II.
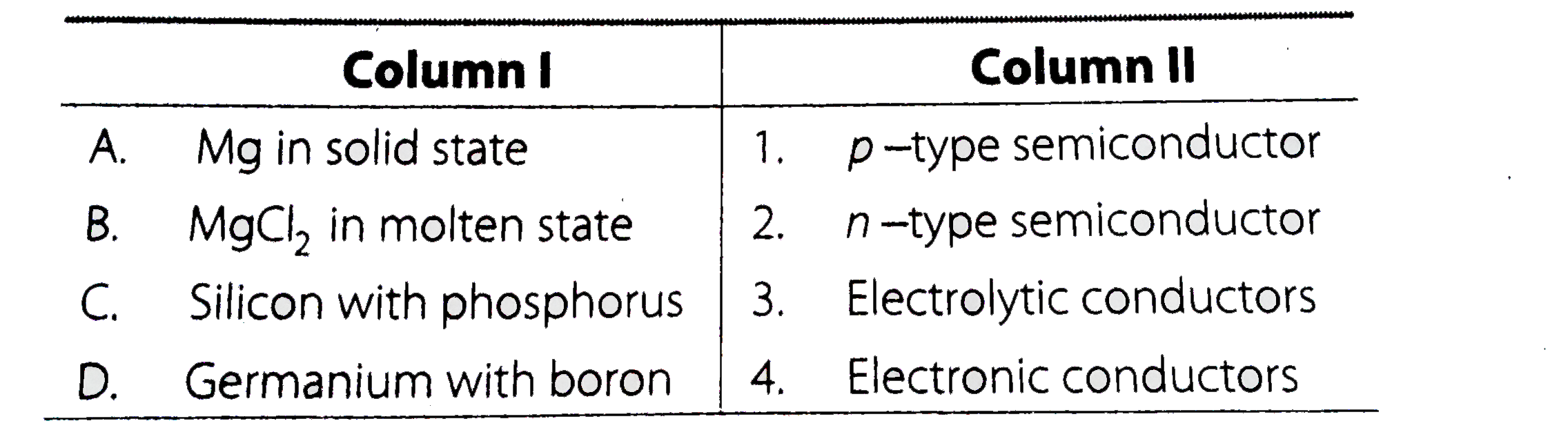
View Solutionmatch the items given in column I with the items given in column II.
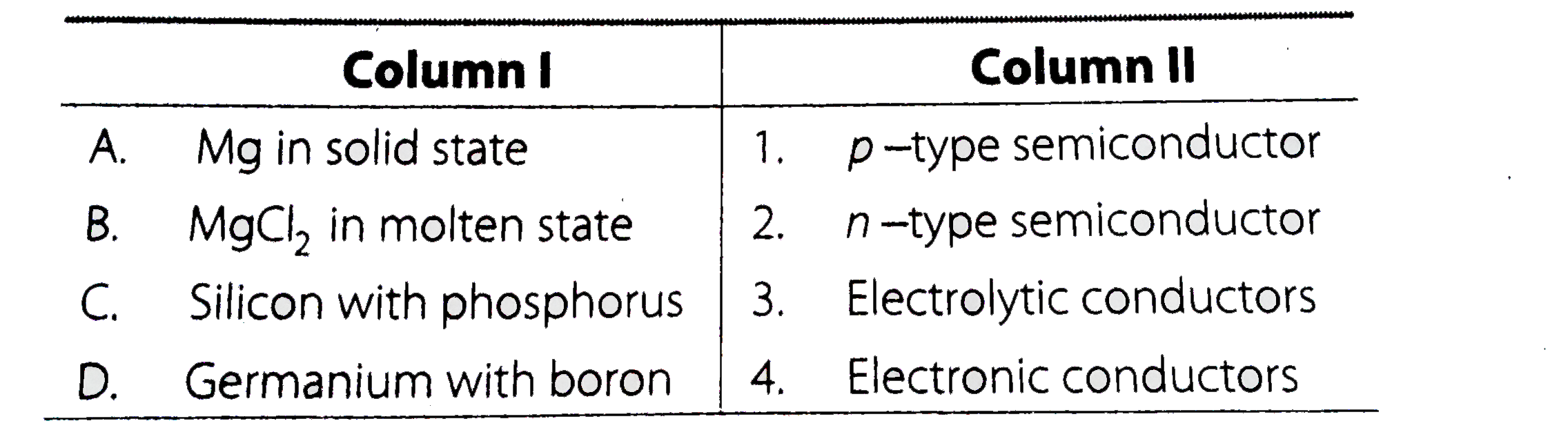
View SolutionMatch the reactions given in Column I with the names given in Column II.
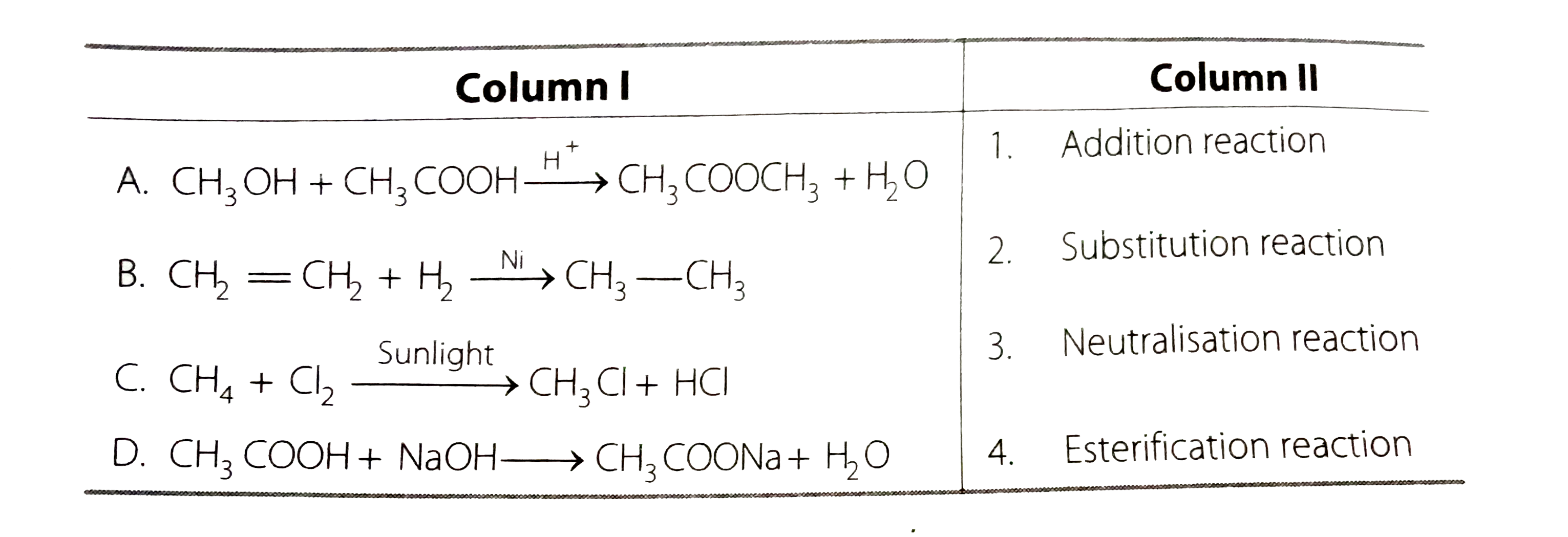
View SolutionMatch materials given in column I with the polymers given in column II

View SolutionMatch the items given in column i with example given in Column II

View SolutionMatch the properties given in Column I with the metals given in Column II.
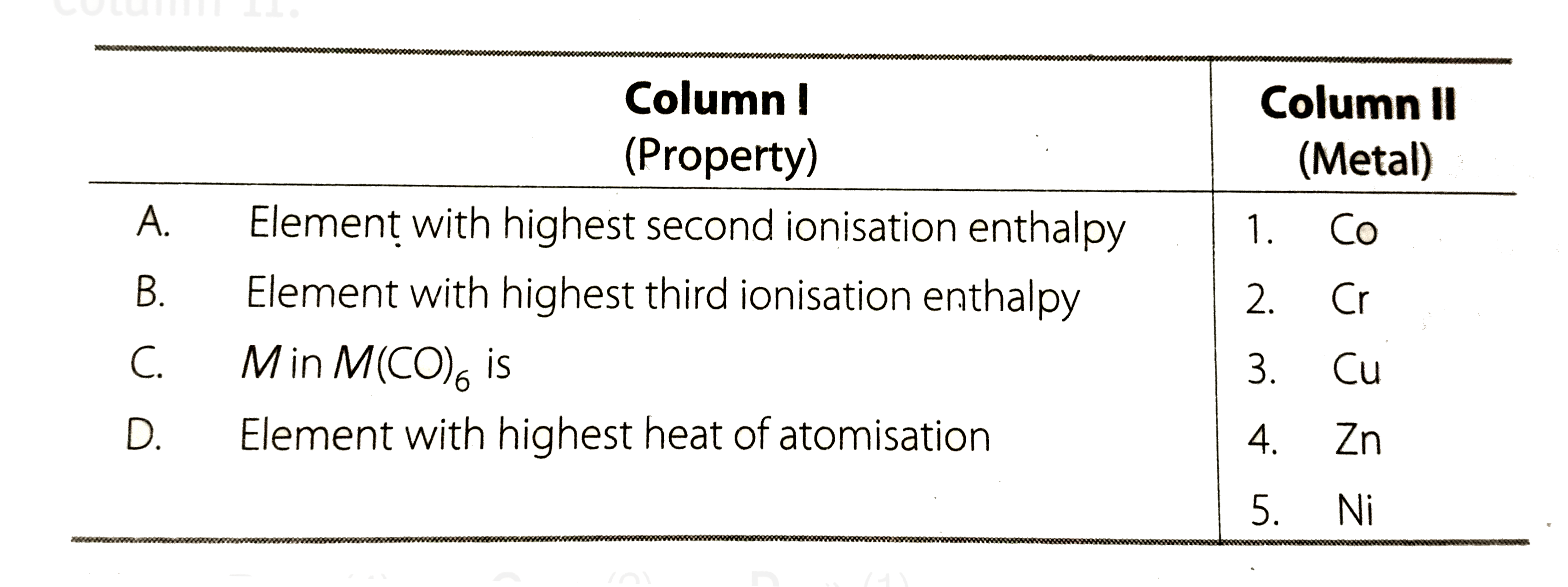
View SolutionMatch the properties given in Column I with the metals given in Column II

View SolutionMatch the property given in Column I with the element given in Column II.

View SolutionMatch the pollutants given in Column I with their effects given in Column II.
View SolutionMatch the compounds given in Column-I with the items given in Column - II.

View Solution