What is the value of rate constant k if the value of the activation energy Ea and the frequency factor A are 49 kJ / mol and 9 × 1010S−1 respectively? (T = 313 K)
6 × 102S−1
9 × 102S−1
3 × 102S−1
6 × 10−2S−1
The correct Answer is:C
To find the value of the rate constant k using the Arrhenius equation, we can follow these steps:
Step 1: Write down the Arrhenius equation
The Arrhenius equation relates the rate constant k to the activation energy Ea, the frequency factor A, and the temperature T:
k=Ae−EaRT
where:
- k = rate constant
- A = frequency factor
- Ea = activation energy
- R = universal gas constant (8.314 J/(mol·K))
- T = temperature in Kelvin
Step 2: Convert activation energy to the correct units
The activation energy Ea is given as 49 kJ/mol. We need to convert this to Joules per mole:
Ea=49kJ/mol=49×103J/mol=49000J/mol
Step 3: Substitute the known values into the equation
Given:
- A=9×1010s−1
- R=8.314J/(mol⋅K)
- T=313K
Now we can substitute these values into the Arrhenius equation:
k=9×1010e−490008.314×313
Step 4: Calculate the exponent
First, calculate the denominator:
RT=8.314×313≈2600.602J/mol
Now calculate the exponent:
−EaRT=−490002600.602≈−18.84
Step 5: Calculate e−EaRT
Now, calculate e−18.84:
e−18.84≈1.3×10−9
Step 6: Calculate the rate constant k
Now substitute this back into the equation for k:
k=9×1010×1.3×10−9≈1.17×102s−1
Step 7: Finalize the result
Thus, the value of the rate constant k is approximately:
k≈117s−1≈1.17×102s−1
Summary
The value of the rate constant k is approximately 117s−1.
---
The Arrhenius equation relates the rate constant k to the activation energy Ea, the frequency factor A, and the temperature T:
k=Ae−EaRT
where:
- k = rate constant
- A = frequency factor
- Ea = activation energy
- R = universal gas constant (8.314 J/(mol·K))
- T = temperature in Kelvin
The activation energy Ea is given as 49 kJ/mol. We need to convert this to Joules per mole:
Ea=49kJ/mol=49×103J/mol=49000J/mol
Given:
- A=9×1010s−1
- R=8.314J/(mol⋅K)
- T=313K
k=9×1010e−490008.314×313
First, calculate the denominator:
RT=8.314×313≈2600.602J/mol
Now calculate the exponent:
−EaRT=−490002600.602≈−18.84
Now, calculate e−18.84:
e−18.84≈1.3×10−9
Now substitute this back into the equation for k:
k=9×1010×1.3×10−9≈1.17×102s−1
Thus, the value of the rate constant k is approximately:
k≈117s−1≈1.17×102s−1
The value of the rate constant k is approximately 117s−1.
Topper's Solved these Questions
Similar Questions
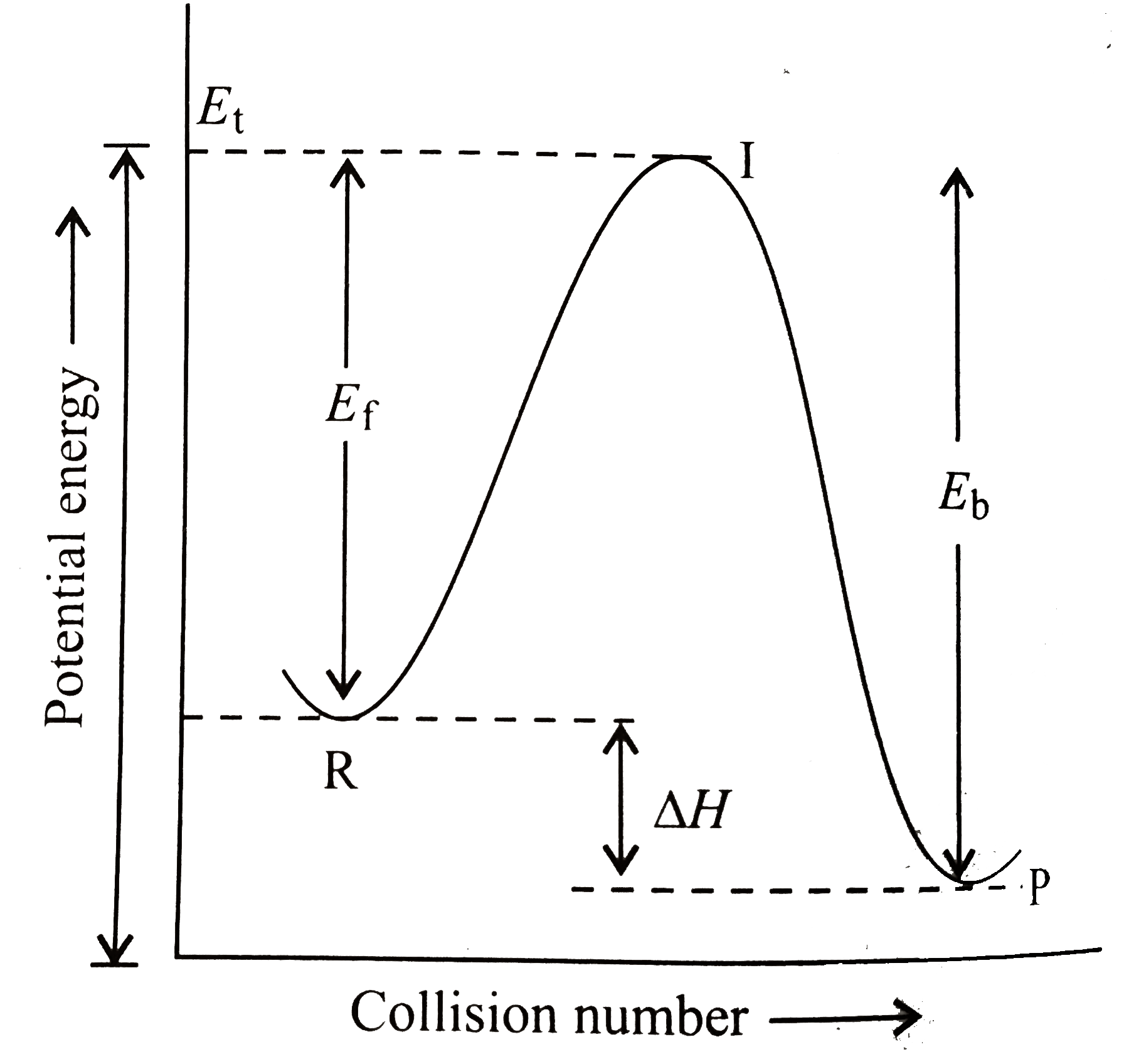
A colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy Ea Large the value of activation energy, smaller the value of rate constant k. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant k.

Ef= Activation energy of forward reaction
Eb= Activation energy of backward reaction
ΔH=Ef−Eb
Ef= threshold energy
In a hypothetical reaction A→B, the activation energies for the forward and backward reactions are 15 and 9kJmol−1, respectively. The potential energy of A is 10kJmol−1. Which of the following is wrong?
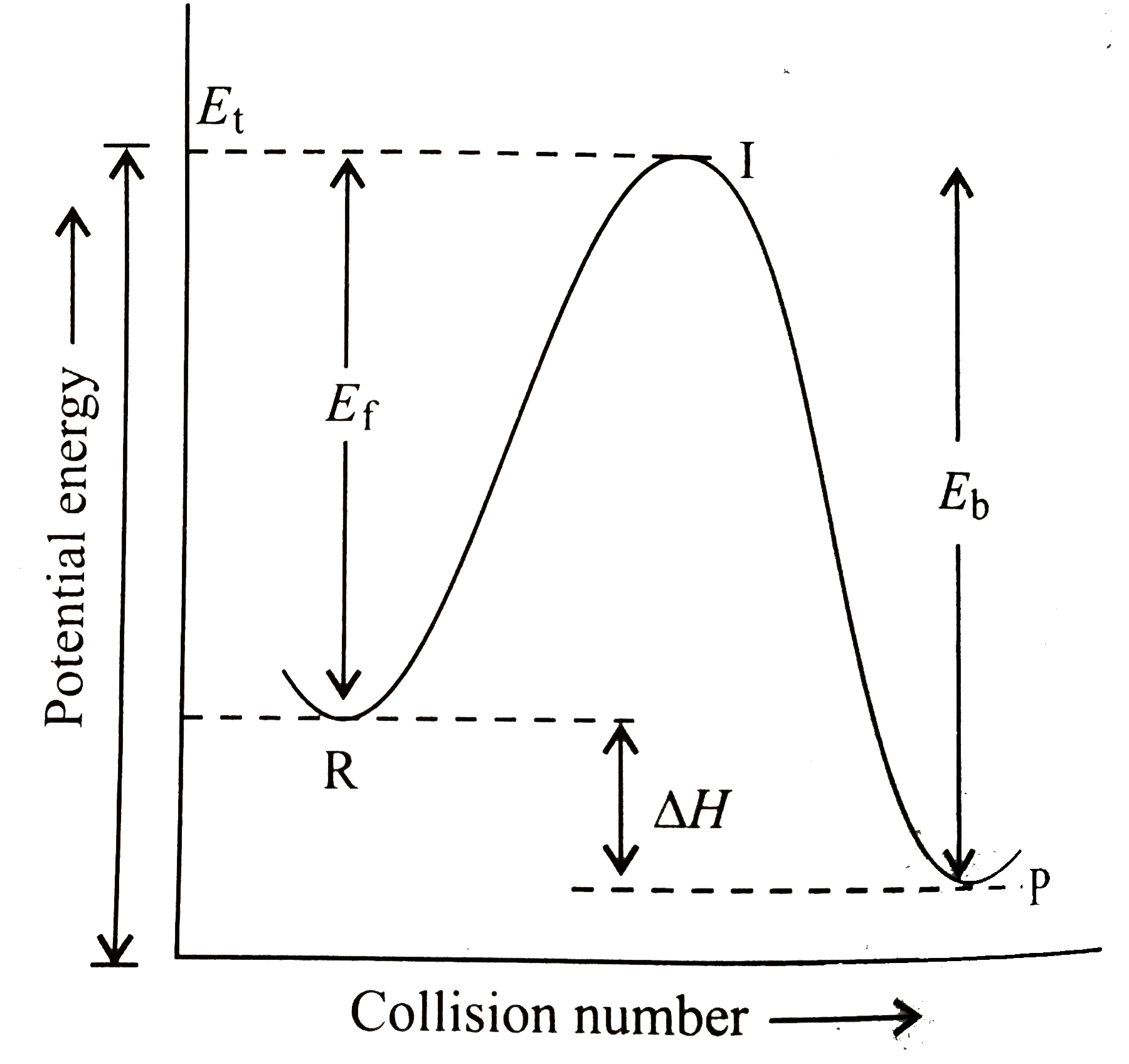
View SolutionA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy Ea Large the value of activation energy, smaller the value of rate constant k. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant k.

Ef= Activation energy of forward reaction
Eb= Activation energy of backward reaction
ΔH=Ef−Eb
Ef= threshold energy
The activation eneries for forward and backward reactions in a chemical reaction are 30.5 and 45.4kJmol−1 respectively. The reaction is
View SolutionA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy Ea Large the value of activation energy, smaller the value of rate constant k. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant k.
Ef= Activation energy of forward reaction
Eb= Activation energy of backward reaction
ΔH=Ef−Eb
Ef= threshold energy
The rate constant of a certain reaction is given by k=Ae−Ea/RT
(where A= Arrhenius constant). Which factor should be lowered so that the rate of reaction may increase?
View SolutionA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy Ea Large the value of activation energy, smaller the value of rate constant k. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant k.
Ef= Activation energy of forward reaction
Eb= Activation energy of backward reaction
ΔH=Ef−Eb
Ef= threshold energy
If a reaction A+B→C is exothermic to the extent 30kJmol−1 and the forward reaction has an activation energy of 249kJmol−1 the activation energy for reverse reaction in kJmol−1 is
View SolutionThe rate constant , the activation energy and Arrhenius parameter of a chemical reaction at 25∘C are x, 10x kJ/ mol and 2xs−1 . Value of rate constant as T→∞ is
View SolutionThe rate constant, activation energy, and Arrphenius parameter of a chemical reaction are 3.0×10−4s−1,104.4KJmol−1, and 6.0×1014s−1, respectively. The value of rate constant as T→∞ is
View SolutionThe rate of decomposition for methyl nitrite and ethyl nitrite can be given in terms of rate constant k1 and k2 respectively. The energy of activation for the two reactions are 152.30kJmol−1 and 157.7kJmol−1 as well as frequency factors are 1013 and 1014 respectively for the decomposition of methyl and ethyl nitrite. Calculate the temperature at which rate constant will be same for the two reactions.
View SolutionIn the Arrhenius equation for a centrain, the value of A and Ea (activation energy ) are 4×1013s−1 and 98.6 kJ mol51 respectively. If the reaction is of first order, at what termperature will its half-life preriod be 10 min ?
View SolutionKp for a reaction at 25∘C is 10 atm. The activation energy for forward and reverse reactions are 12 and 20kJmol−1 respectively. The Kc for the reaction at 40∘C will be:
View SolutionFor a reaction the activation energy Ea=0 and the rate constant=3.2×106sec−1 at 300K. What is the value of rate constant at 310K?
View Solution
