Addition of two vectors, is represented in which of the following options correctly?
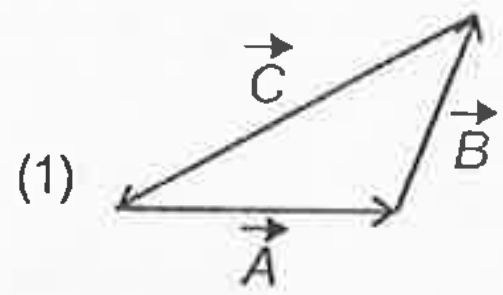
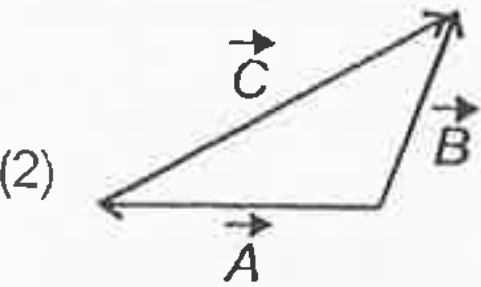
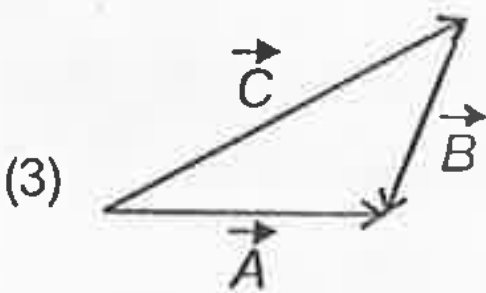
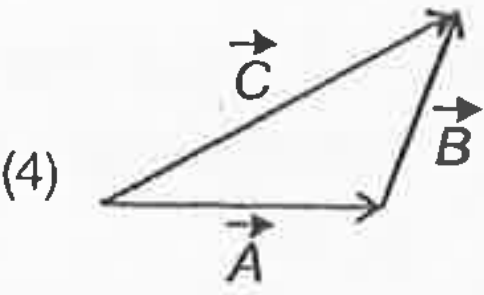
The correct Answer is:D
To solve the question regarding the addition of two vectors →A+→B=→C and to determine which option represents this correctly, we can follow these steps:
1. Understanding Vector Addition:
- Vector addition can be visualized using the triangle law of vector addition. According to this law, if two vectors are represented as two sides of a triangle, the resultant vector is represented by the third side of the triangle.
2. Drawing the Vectors:
- Start by drawing the first vector →A. This vector can be drawn as an arrow starting from a point O and pointing to a point A.
- Next, draw the second vector →B. This vector should start from the head (the endpoint) of the first vector →A. So, if →A ends at point A, then →B should start from point A and point to another point B.
3. Identifying the Resultant Vector:
- The resultant vector →C is drawn from the tail of the first vector →A (which is point O) to the head of the second vector →B (which is point B). This vector →C represents the sum of →A and →B.
4. Analyzing the Options:
- Now, we need to look at the provided options and see which one correctly represents this arrangement.
- Check each option to see if →A starts at a point, →B starts at the head of →A, and →C connects the tail of →A to the head of →B.
5. Selecting the Correct Option:
- After analyzing the options, identify the one that matches the arrangement described above. The correct option will show →A leading into →B and →C as the resultant vector.
- Vector addition can be visualized using the triangle law of vector addition. According to this law, if two vectors are represented as two sides of a triangle, the resultant vector is represented by the third side of the triangle.
- Start by drawing the first vector →A. This vector can be drawn as an arrow starting from a point O and pointing to a point A.
- Next, draw the second vector →B. This vector should start from the head (the endpoint) of the first vector →A. So, if →A ends at point A, then →B should start from point A and point to another point B.
- The resultant vector →C is drawn from the tail of the first vector →A (which is point O) to the head of the second vector →B (which is point B). This vector →C represents the sum of →A and →B.
- Now, we need to look at the provided options and see which one correctly represents this arrangement.
- Check each option to see if →A starts at a point, →B starts at the head of →A, and →C connects the tail of →A to the head of →B.
- After analyzing the options, identify the one that matches the arrangement described above. The correct option will show →A leading into →B and →C as the resultant vector.
Topper's Solved these Questions
Similar Questions
If →a,→band→c are three vectors of which every pair is non colinear. If the vector →a+→band→b+→c are collinear with the vector →c and →a respectively then which one of the following is correct? (A) →a+→b+→c is a nul vector (B) →a+→b+→c is a unit vector (C) →a+→b+→c is a vector of magnitude 2 units (D) →a+→b+→c is a vector of magnitude 3 units
View SolutionLet →a,→b,→c be unit vectors such that →a+→b+→c=→0. Which of the following is correct?
View SolutionTwo vectors →A and →B are such that →A+→B=→C and A2+B2=C2. Which of the following statements, is correct:-
View SolutionIf →A×→B=→C, then choose the incorrect option : [→Aand→B are non zero vectors]
View SolutionIf →a,→band→c are three non-zero, non-coplanar vectors,then find the linear relation between the following four vectors : →a−2→b+3→c,2→a−3→b+4→c,3→a−4→b+5→c,7→a−11→b+15→c.
View SolutionThe vector (→a.→b)→c−(→a.→c)→b is perpendicular to
View SolutionTwo vectors →a and →b add to give a resultant →c=→a+→b. In which of these cases angle between →a and →b is maximum: (a,b,c represent the magnitudes of respective vectors )
View SolutionLet →A,→Band→C be vectors of legth , 3,4and 5 respectively. Let →A be perpendicular to →B+→C,→B to →C+→Aand→C to→A+→B then the length of vector →A+→B+→C is __________.
View SolutionIf →a,→band→c are non - zero vectors such that →a.→b=→a.→c,then find the goemetrical relation between the vectors.
View SolutionIf →aand→b be two non collinear vectors such that →a=→c+→d, where →c is parallel to →b and →d is perpendicular to →b obtain expression for →cand→d in terms of →aand→b as: →d=→a−(→a.→b)→bb2,→c=(→a.→b)→bb2
View Solution
