a bus is moving towards and stationary observer with speed 20 m/s blows a horn of frequency 200 Hz. the frequency of sound heard by the observer is approximately ( take speed of sound 320 m/s)
188 Hz
200 Hz
226 Hz
213 Hz
The correct Answer is:D
To solve the problem of finding the frequency of sound heard by a stationary observer when a bus is moving towards them, we can use the Doppler effect formula. Here’s the step-by-step solution:
Step 1: Identify the given values
- Frequency of the sound emitted by the bus (source), f0=200Hz
- Speed of the bus (source), vs=20m/s
- Speed of sound in air, v=320m/s
- Speed of the observer, vo=0m/s (since the observer is stationary)
Step 2: Write the formula for the apparent frequency
The formula for the apparent frequency f heard by the observer when the source is moving towards a stationary observer is given by:
f=f0×v+vov−vs
Step 3: Substitute the values into the formula
Since the observer is stationary, vo=0. Therefore, the formula simplifies to:
f=f0×vv−vs
Substituting the known values:
f=200Hz×320m/s320m/s−20m/s
Step 4: Calculate the denominator
Calculate 320m/s−20m/s:
320m/s−20m/s=300m/s
Step 5: Substitute back into the formula
Now substitute back into the formula:
f=200Hz×320m/s300m/s
Step 6: Simplify the fraction
Now simplify the fraction:
f=200Hz×3230
Step 7: Calculate the apparent frequency
Now calculate the frequency:
f=200Hz×3230=200Hz×1.0667≈213.33Hz
Step 8: Round to the nearest whole number
The approximate frequency heard by the observer is:
f≈213Hz
Final Answer
The frequency of sound heard by the observer is approximately 213 Hz.
---
- Frequency of the sound emitted by the bus (source), f0=200Hz
- Speed of the bus (source), vs=20m/s
- Speed of sound in air, v=320m/s
- Speed of the observer, vo=0m/s (since the observer is stationary)
The formula for the apparent frequency f heard by the observer when the source is moving towards a stationary observer is given by:
Since the observer is stationary, vo=0. Therefore, the formula simplifies to:
Calculate 320m/s−20m/s:
Now substitute back into the formula:
Now simplify the fraction:
Now calculate the frequency:
The approximate frequency heard by the observer is:
The frequency of sound heard by the observer is approximately 213 Hz.
Topper's Solved these Questions
Similar Questions
a bus is moving in a circle around a listener with speed 20 m/s of radius 2 m. Bus driver blows a horn with frequency 210 Hz. the frequency of sound heard by the listener is
View SolutionA train is moving with speed 72 km/h towards a hill blows a whistle of frequency 1240Hz. the frequency of echo heard by driver is(speed of sound=330m/s)
View Solution
Knowledge Check
A sound source is moving towards a stationary observer with 1/10 of the speed of sound. The ratio of apparent to real frequency is
A109B(109)2C(1110)2D1110
A train moves towards a stationary observer with speed 34 m/s. The train sounds a whistle and its frequency registered by the observer is f1. If the speed of train is reduced to 17 m/s, the frequency registered is f2. If speed fo sound is 340 m/s, then the ratio f1/f2 is :
View SolutionA car is moving towards a fixed wall, it blows form of frequency of 440Hz . The frequency of reflected sound observed by the driver is 480Hz then find the speed of car in km/hr. (Speed of sound is 350msec
View SolutionA source of sound is travelling towards a stationary observer. The frequency of sound heard by the observer is 25% more that the actual frequency. If the speed of sound is v, that of the source is
View SolutionA train moves towards a stationary observer with speed 34m/s. The train sounds a whistle and its frequency registered by the observer is f1. If the train's speed is reduced to 17m/s, the frequency registered is f2. If the speed of sound of 340m/s, then the ratio f1/f2is
View SolutionA train moves towards a stationary observer with speed 34m/s. The train sounds a whistle and its frequency registered by the observer is f1. If the train's speed is reduced to 17m/s, the frequency registered is f2. If the speed of sound of 340m/s, then the ratio f1/f2is
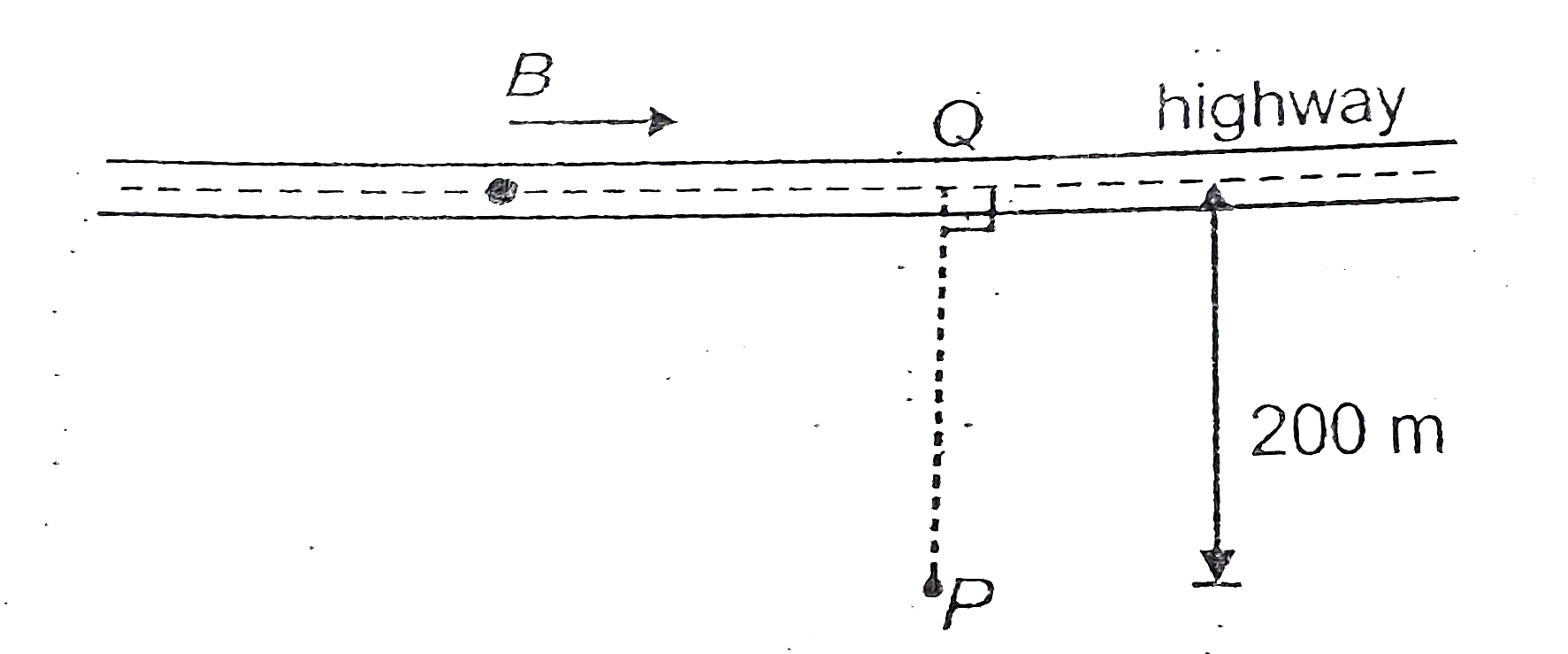
View SolutionA person P is standing at a perpendicular distance of 200m from point Q on a highway. A bus B is moving with a speed of 42.43ms−1 towards point Q on the highway. The driver of the bus blows a horn of frequency 1300 Hz. What is the frequency of sound received by the person P, when the bus is distant 200 m from Q. speed of sound in air is 330ms−1
View SolutionA source is moving towards an observer with a speed of 20 m / s and having frequency of 240 Hz . The observer is now moving towards the source with a speed of 20 m / s . Apparent frequency heard by observer, if velocity of sound is 340 m / s , is
View Solution
