The resistivity of a wire at 20∘C and 100∘C is 3Ω−m and 4Ω−m respectively. The resistivity of the wire at 0∘C is
114Ω−m
411Ω−m
34Ω−m
113Ω−m
The correct Answer is:A
Step by step video & image solution for The resistivity of a wire at 20^circ C and 100^circ C is 3 Omega-m and 4 Omega-m respectively. The resistivity of the wire at 0^circ C is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
In a platinum resistance thermometer resitance of the platinum wire at 0∘C,100∘C and in hot bath are 8Ω,12Ω and 11Ω respectively. Temperature of hot bath is
View SolutionThe resistances of an iron wire and a copper wire at 20∘Care 3.9(Ω)and 4.1(Ω)respectively. At what temperature will the resistances be equal?Temperature coefficient of resistivity for iron is 5.0×10−3K−1and for copper it is 4.0×10−3k−1.Neglect any thermal expansion.
View Solution
Knowledge Check
- Question 1 - Select One
A wire has a resistance of 2.5Ωat28∘C and a resistance of 2.9Ωat100∘C. The temperature coefficient of resistivity of material of the wire is
A1.06×10−3.∘C−1B3.5×10−2.∘C−1C2.22×10−3.∘C−1D9.95×10−2.∘C−1
A wire AB (of length 1m, area of cross section πm2) is used in potentiometer experiment to calculate emf and internal resistance (r) of battery.
The emf and internal resistance of driving battery are 15 V and 3Ω respectively.The resistivity of wire AB varies as ρ=ρ0x (where x is distance form A in meters and ρ0=24πΩ)
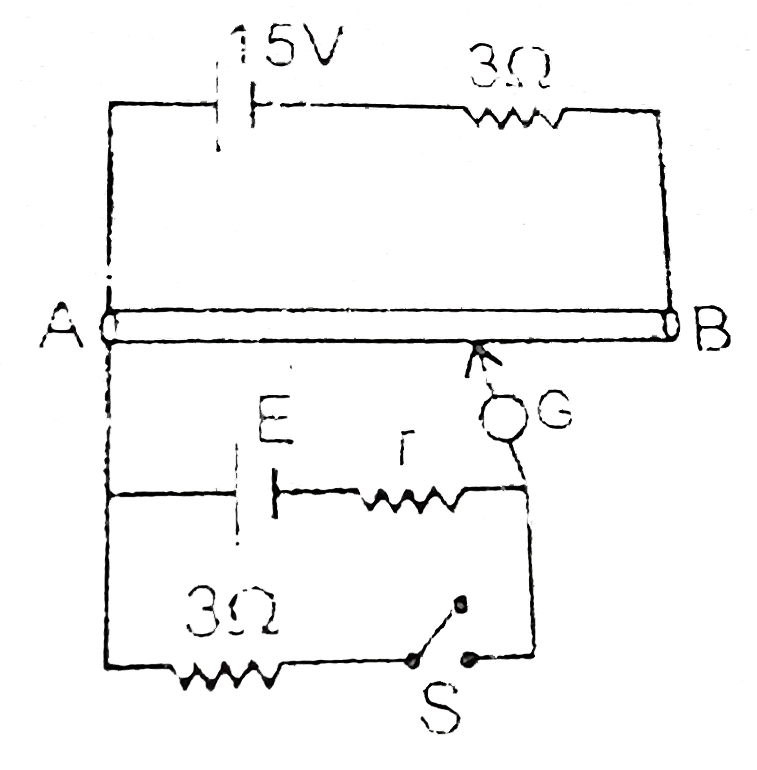
The distance of null point from A obtained at √23m when switch 'S' is open and at 1√2m m when switch is closed.
The resistance of whole wire AB is-View SolutionThe resistance of a wire at 20∘C is 20Ω and at 500∘C is 60Ω. At which temperature its resistance will be 25Ω?
View SolutionThe resistance of the four arms A, B, C and D of a wheatstone bridge as shown in the figure are 10Ω, 20Ω ,30Ω and 60Ω respectively . The emf and internal resistance of the cell are 15V and 2.5Ω respectively . If the galvanometer resistance is 80Ω then the net current drawn from the cell will be
_PHY_E05_111_Q01.png)
View SolutionTwo resistors with temperature coefficient of 3 resistances 4⋅10−3/°C and 2⋅10−3/°C have of resistances 20 Omega and 10 Omega respectively at 0°C. If they are connected in series, then equivalent temperature coefficient of resistor combination is
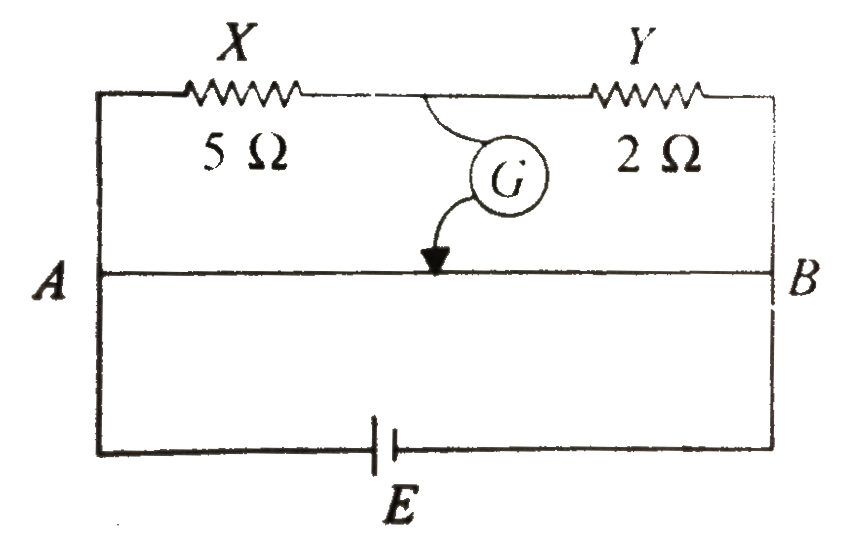
View SolutionIn the simple potentionmeter circuit, where the length AB of the potentiometer wire is 1m, the resistors X and Y have values of 5Ω and 2Ω, respectively. When X is shunted by a wire, the balance point is found to be 0.625m from A. What is the resistance of the shunt?
View SolutionThe temperature coefficient of resistance of a wire is 0.00145∘C−1. At 100∘C its resistance is 2Ω. At what temperature the resistance of the wire be 3Ω?
View SolutionResistance of tungsten wire at 150∘C is 133Ω. Its resistance temperature coefficient is 0.0045/∘C. The resistance of this wire at 500∘C will be
View Solution