If a convex lens of refractive index μl is placed in a medium of refractive index μm Such that μl>μm>μair then
The nature of the lens is diverging
The nature of the lens is converging
The nalure of the lens may be converging or diverging
The nature of the lens can't be determined
The correct Answer is:B
To solve the problem step by step, we will use the lens maker's formula and analyze the conditions given in the question.
1. Understanding the Given Information:
- We have a convex lens with a refractive index μl.
- The lens is placed in a medium with a refractive index μm.
- The conditions given are μl>μm>μair.
2. Lens Maker's Formula:
- The lens maker's formula is given by:
1f=(μlμm−1)(1R1−1R2)
- Here, f is the focal length of the lens, R1 and R2 are the radii of curvature of the lens surfaces.
3. Analyzing the Condition:
- Since μl>μm, we can say:
μlμm>1
- This implies that:
μlμm−1>0
- Therefore, the term (μlμm−1) is positive.
4. Nature of the Lens:
- For a convex lens, the term (1R1−1R2) is also positive because R1 (the radius of curvature of the first surface) is positive and R2 (the radius of curvature of the second surface) is negative.
- Thus, both terms in the lens maker's formula are positive, leading to:
1f>0
- This means that the focal length f is positive.
5. Conclusion:
- A positive focal length indicates that the lens is converging. Therefore, the nature of the lens is converging.
Final Answer:
The nature of the lens is converging.
- We have a convex lens with a refractive index μl.
- The lens is placed in a medium with a refractive index μm.
- The conditions given are μl>μm>μair.
- The lens maker's formula is given by:
1f=(μlμm−1)(1R1−1R2)
- Here, f is the focal length of the lens, R1 and R2 are the radii of curvature of the lens surfaces.
- Since μl>μm, we can say:
μlμm>1
- This implies that:
μlμm−1>0
- Therefore, the term (μlμm−1) is positive.
- For a convex lens, the term (1R1−1R2) is also positive because R1 (the radius of curvature of the first surface) is positive and R2 (the radius of curvature of the second surface) is negative.
- Thus, both terms in the lens maker's formula are positive, leading to:
1f>0
- This means that the focal length f is positive.
- A positive focal length indicates that the lens is converging. Therefore, the nature of the lens is converging.
The nature of the lens is converging.
Topper's Solved these Questions
Similar Questions
A double convex lens of refractive index m1 is immersed in a liquid of refractive index m2. This lens will act as:
View SolutionA sphere of radius R made of material of refractive index μ2 is placed in a medium of refractive index μ1. Where would an object be placed so that a real image is formed at equidistant fromk the sphere? ltbgt
View Solution
Knowledge Check
A double convex lens, lens made of a material of refractive index μ1, is placed inside two liquids or refractive indices μ2 and μ3, as shown. μ2>μ1>μ3. A wide, parallel beam of light is incident on the lens from the left. The lens will give rise to
 Aa single convergent beamBtwo different convergent beamsCtwo different divergent beamsDa convergent and a divergent beam.
Aa single convergent beamBtwo different convergent beamsCtwo different divergent beamsDa convergent and a divergent beam.
A thin bi-convex lens made out of a material of refractive index μ1 is place in a medium of refractive index μ2. A paraxial beam of light, parallel to the principal axis of the lens, is shown in the figure. Based on the ray diagram, we can conclude that

View SolutionThe adjacent figure shows a thin plano-convex lens of refractive index μ1 and a thin plano-concave lens of refractive index μ2, both having same radius of curvature R of their curved surfaces. The thin lens of refractive index μ3 has radius of curvature R of both its surfaces. This lens is so placed in between the plano-convex and plano-concave lenses that the plane surfaces are parallel to each other.
The focal length of the combination is

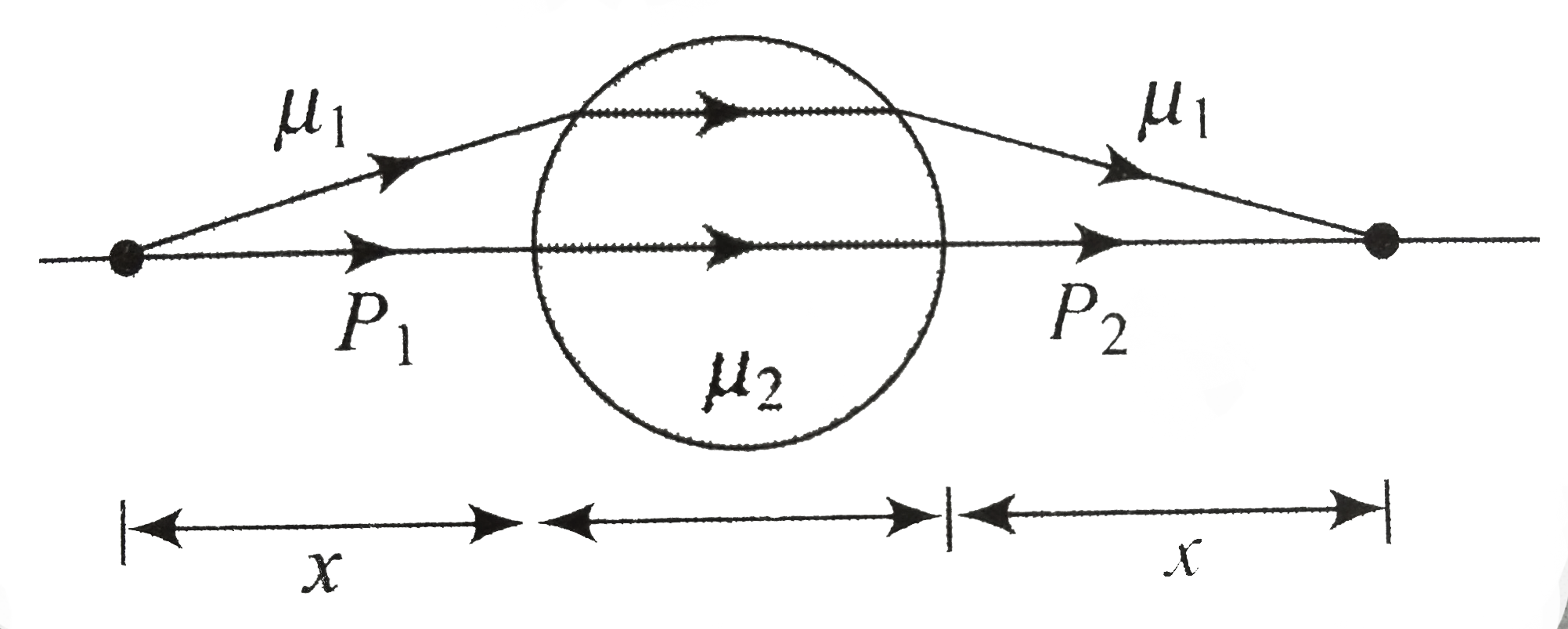
View SolutionA right angled prism of refractive index μ1 is placed in a rectangular block of refractive index μ2 , which is surrounded by a medium of refractive index μ3 ,as shown in the figure . A ray of light 'e' enters the rectangular block at normal incidence . depending upon the relationship between μ1,μ2andμ3 , it takes one of the four possible paths 'ef' , 'eg' , 'eh' or 'ef'
_E01_228_Q01.png)
Match the paths in List I with conditions of refractive indices in List II and select the correct answer using the codes given below the lists:
{:("List" I , "List" II) , ( P. e rarr f , 1. mu_(1)gt sqrt(2mu_(2))) , ( Q. e rarr g , 2. mu_(2) gt mu_(1) "and" mu_(2) gt mu_(3)), ( R. e rarr f , 3. mu_(1) = mu_(2)), ( S. e rarr f , 4. mu_(2) lt mu_(1) lt sqrt(2mu_(2)) "and" mu_(2) gt mu_(3)):}<br>Codes:<br>{:( P , Q , R , S) , ((A) 2 , 3 , 1 , 4), ((B) 1 , 2 , 4 , 3) , ((C) 4 , 1 , 2 , 3) , ((D) 2, 3 , 4 , 1):}
View SolutionStatement-1 : A glass convex lens (refractive index, μ1=1.5), when immersed in a liquid of refractive index μ2=2, functions as a diverging lens.
Statement-2 : The focal length of a lens is given by 1f=(μ−1)(1R1−1R2), where μ is the relative refractive index of the material of the lens with respect to the surrounding medium.
View SolutionA transparent cube of side d, made of a material of refractive index μ2 , is immersed in a liquid of refractive index μ1(μ1<μ2). . A ray is incident on the face AV at an angle θ (shown in the figure). Total internal refraction takes place at point E on the face BC. Then must satisfy:
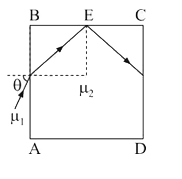
View SolutionA transparent cube of side d, made of a material of refractive index μ2 , is immersed in a liquid of refractive index μ1(μ1<μ2). . A ray is incident on the face AV at an angle θ (shown in the figure). Total internal refraction takes place at point E on the face BC. Then must satisfy:

View SolutionA thin lens made of a material of refractive indexμ2 has a medium of refractive index μ1 on one side and a medium of refractive index on the other side. The lens is biconvex and the two radii of curvature have equal magnitude R. A beam of light travelling parallel to the principal axis is incident on the lens. Where will the image be formed if the beam is incident from (a) the medium p, and (b) from the medium μ3?
View Solution
