Calculate the value of Rydberg's constant.
1.097×107m−1
8.85×10−12m−1
1.6×10−19m−1
6.63×10−34m−1
The correct Answer is:A
To calculate the value of Rydberg's constant (R), we can use the formula:
R=2π2me4h3c
where:
- m is the mass of the electron,
- e is the charge of the electron,
- h is Planck's constant,
- c is the speed of light.
Step 1: Identify the constants needed for the calculation
- Mass of the electron, m=9.1×10−31 kg
- Charge of the electron, e=1.6×10−19 C
- Speed of light, c=3×108 m/s
- Planck's constant, h=6.63×10−34 J·s
- Value of π≈3.14
Step 2: Substitute the values into the formula
Substituting the values into the formula, we have:
R=2×(3.14)2×(9.1×10−31)×(1.6×10−19)4(6.63×10−34)3×(3×108)
Step 3: Calculate the numerator
First, calculate the numerator:
1. Calculate (3.14)2:
(3.14)2≈9.8596
2. Calculate (1.6×10−19)4:
(1.6)4=6.5536and(10−19)4=10−76⇒(1.6×10−19)4=6.5536×10−76
3. Now, calculate the entire numerator:
2×9.8596×(9.1×10−31)×(6.5536×10−76)
Performing the multiplication:
≈2×9.8596×9.1×6.5536×10−31−76≈2×9.8596×9.1×6.5536×10−107
This gives us a numerical value for the numerator.
Step 4: Calculate the denominator
Now calculate the denominator:
1. Calculate (6.63×10−34)3:
(6.63)3≈291.61and(10−34)3=10−102⇒(6.63×10−34)3≈291.61×10−102
2. Now multiply by 3×108:
291.61×10−102×3×108=874.83×10−94
Step 5: Final calculation
Now we can finalize the calculation of R:
R=NumeratorDenominator≈Value from Step 3874.83×10−94
After performing the division, we find:
R≈1.097×107m−1
Conclusion
The value of Rydberg's constant is approximately 1.097×107m−1.
---
- m is the mass of the electron,
- e is the charge of the electron,
- h is Planck's constant,
- c is the speed of light.
- Mass of the electron, m=9.1×10−31 kg
- Charge of the electron, e=1.6×10−19 C
- Speed of light, c=3×108 m/s
- Planck's constant, h=6.63×10−34 J·s
- Value of π≈3.14
Substituting the values into the formula, we have:
First, calculate the numerator:
(3.14)2≈9.8596
(1.6)4=6.5536and(10−19)4=10−76⇒(1.6×10−19)4=6.5536×10−76
2×9.8596×(9.1×10−31)×(6.5536×10−76)
≈2×9.8596×9.1×6.5536×10−31−76≈2×9.8596×9.1×6.5536×10−107
Now calculate the denominator:
(6.63)3≈291.61and(10−34)3=10−102⇒(6.63×10−34)3≈291.61×10−102
291.61×10−102×3×108=874.83×10−94
Now we can finalize the calculation of R:
The value of Rydberg's constant is approximately 1.097×107m−1.
Topper's Solved these Questions
Similar Questions
Calculate the value of universal gas constant at STP.
View SolutionWhat is the energy difference and the frequency of light emitted when the electron in a hydrogen atom undergoes transition from the energy level n=4 to the energy n=3 given that the value of Rydberg constant is 1.0974×107m−1?
View SolutionThe electon, in a hydrogen atom, is in its second excited state. Calculate the wavelength of the lines in the Lyman series, that can be emitted through the permisible transitions of this electron.
Given the value of Rydberg constant, R=1.1×107m−1)
View SolutionUsing Bohr's postulates, derive the expression for the total energy of the electron revolving in nth orbit of hydrogen atom. Find the wavelength of Hα line, given the value of Rydberg constant, R=1.1×107m1
View SolutionThe value of solar constant is
View SolutionThe value of Planck's constant is
View SolutionCalculate the Rydberg constant RH if He+ ions are known to have the wavelength difference between the from ( of the longest wavength ) lines fo Balmer and Lyman series equal to 133.7nm.
View SolutionFrom the following data for the decomposition of azoisopropane at 543 K into hexane and nitrogen, calculate the average value of rate constant and also show that it is a first order reaction.
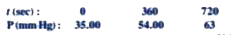
View SolutionFrom the following data for the decomposition of azoisopropane at 543 K into hexane and nitrogen, calculate the average value of rate constant and also show that it is a first order reaction.
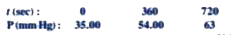
View SolutionFrom the following data for the decomposition of azoisopropane at 543 K into hexane and nitrogen, calculate the average value of rate constant and also show that it is a first order reaction.
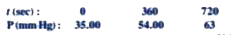
View Solution
