Which of the following can be correct?
ΔH - ΔU = ΔnRT
Cp−Cv=R
(dHdT)p−(dUdT)v= R
All of these
To solve the question, we need to analyze each of the given options one by one to determine their correctness.
1. Option 1: ΔH - ΔU = ΔnRT
- We start with the definition of enthalpy (ΔH):
ΔH=ΔU+PΔV
- We also know from the ideal gas law that:
PV=nRT⟹PΔV=ΔnRT
- Substituting this into the enthalpy equation gives:
ΔH=ΔU+ΔnRT
- Rearranging this, we find:
ΔH−ΔU=ΔnRT
- Therefore, Option 1 is correct.
2. Option 2: Cp - Cv = R
- We know that:
Cp=(dHdT)PandCv=(dUdT)V
- From the relationship between enthalpy and internal energy, we have:
H=U+PV
- Differentiating with respect to temperature gives:
dHdT=dUdT+d(PV)dT
- Using the ideal gas law, we can express PV as nRT:
d(PV)dT=R(for 1 mole of gas)
- Thus, we have:
Cp=Cv+R
- Rearranging gives:
Cp−Cv=R
- Therefore, Option 2 is correct.
3. Option 3: ΔHΔT at constant pressure - ΔUΔT at constant volume = R
- We know from the definitions:
ΔHΔT=CpandΔUΔT=Cv
- From the previous result, we have:
Cp−Cv=R
- Therefore:
ΔHΔT−ΔUΔT=R
- Thus, Option 3 is correct.
4. Conclusion:
- Since all three options (1, 2, and 3) are correct, we conclude that:
Option 4: All of these is correct.
Final Answer:
The correct answer is Option 4: All of these.
- We start with the definition of enthalpy (ΔH):
ΔH=ΔU+PΔV
- We also know from the ideal gas law that:
PV=nRT⟹PΔV=ΔnRT
- Substituting this into the enthalpy equation gives:
ΔH=ΔU+ΔnRT
- Rearranging this, we find:
ΔH−ΔU=ΔnRT
- Therefore, Option 1 is correct.
- We know that:
Cp=(dHdT)PandCv=(dUdT)V
- From the relationship between enthalpy and internal energy, we have:
H=U+PV
- Differentiating with respect to temperature gives:
dHdT=dUdT+d(PV)dT
- Using the ideal gas law, we can express PV as nRT:
d(PV)dT=R(for 1 mole of gas)
- Thus, we have:
Cp=Cv+R
- Rearranging gives:
Cp−Cv=R
- Therefore, Option 2 is correct.
- We know from the definitions:
ΔHΔT=CpandΔUΔT=Cv
- From the previous result, we have:
Cp−Cv=R
- Therefore:
ΔHΔT−ΔUΔT=R
- Thus, Option 3 is correct.
- Since all three options (1, 2, and 3) are correct, we conclude that:
Option 4: All of these is correct.
The correct answer is Option 4: All of these.
Similar Questions
A complex cation is formed by Pt( in some oxidation state ) with ligands ( in proper number so that coordination number of Pt becomes six ). Which of the following can be its correct IUPAC name ?
View SolutionA complex anion is formed by Osmium ( in some oxidation state ) with ligands ( in proper number so that coordination number of osmium becomes six ). Which of the following can be its correct IUPAC name ?
View Solution
Knowledge Check
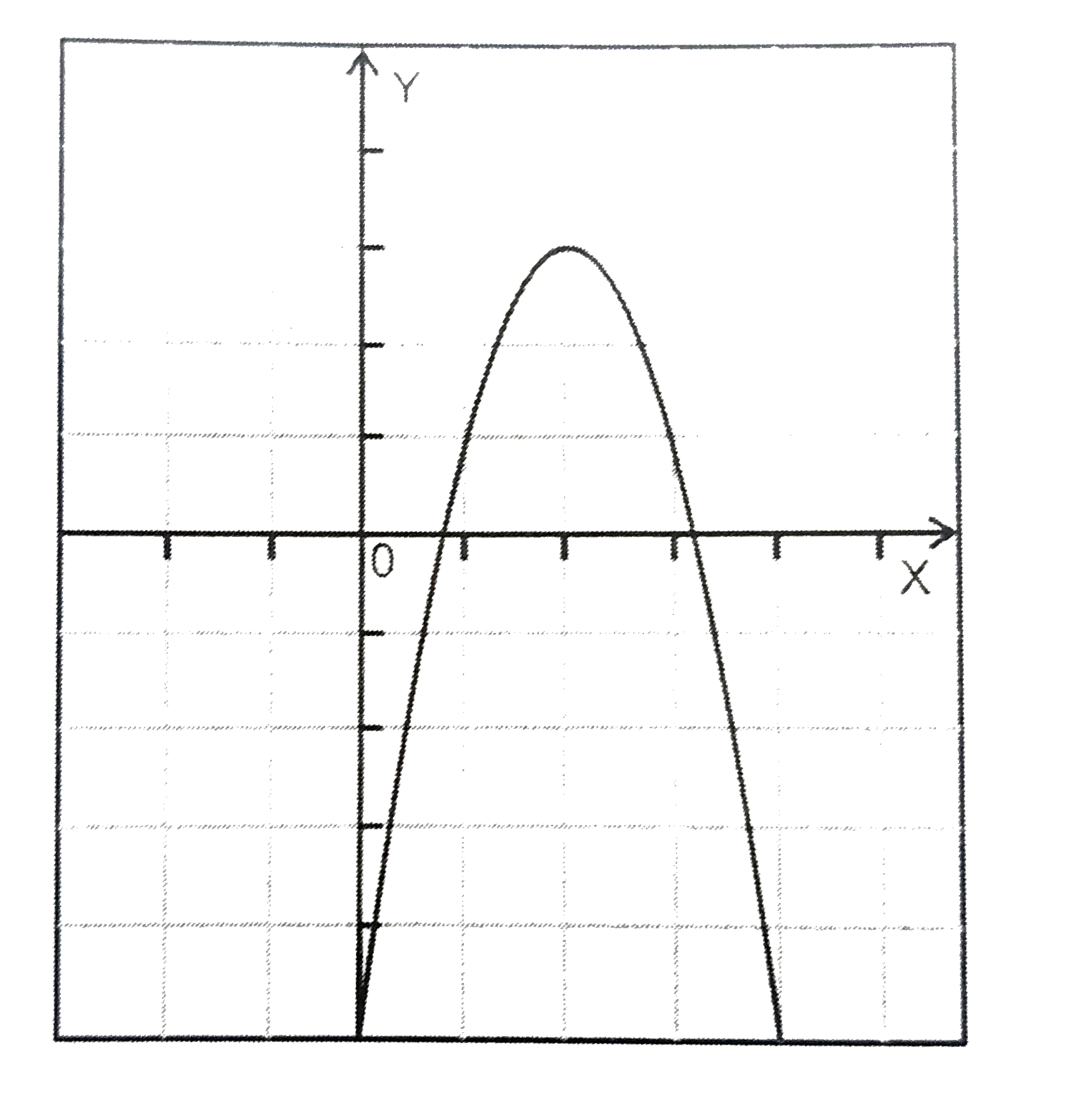
Which of the following can be the correct expression for the graph of the quadratic shown above ?Ay=x2−6x+8By=−x2+6x−8Cy=x2+6x−8Dy=−x2+6x+8Which of the following is not correct?
AN⊂RBN⊂QCQ⊂RDN⊂TWhich of the following is not correct?
AGe(OH)2 is amphotericBGeCl2 is more stable than GeCl4CGeO2 is weakly acidicDGeCl4 in HCl forms [GeCl6]2− ion
Which of the following are correct ?
View SolutionWhich of the following is/are correct?
View SolutionIn nature, a symbiotic association is found between an algae and a fungus. Which of the following can be regarded as the correct property for this association?
View SolutionWhich of the following is not correct?
View SolutionWhich of the following is not correct?
View Solution
