pH of a strong acid solution is 2. What volume of water must be added to its 1L of solution so that pH of new solution becomes 3?
1L
2L
10L
9L
To solve the problem, we need to determine how much water must be added to a 1L solution of a strong acid with a pH of 2 so that the pH of the new solution becomes 3.
1. Determine the initial concentration of H⁺ ions:
- The pH of the initial solution is 2.
- Using the formula pH=−log(H+), we can find the concentration of H⁺ ions.
- (H+)=10−pH=10−2=0.01M
2. Calculate the number of moles of H⁺ ions in the initial solution:
- The volume of the initial solution is 1L.
- Moles of H⁺ ions can be calculated using the formula:
- Moles=Molarity×Volume=0.01mol/L×1L=0.01mol
3. Determine the concentration of H⁺ ions for the final solution:
- The desired pH of the new solution is 3.
- Again using the formula pH=−log(H+):
- (H+)=10−3=0.001M
4. Set up the equation for the final solution:
- Let V be the final volume of the solution after adding water.
- The number of moles of H⁺ ions remains the same (0.01 mol), but the concentration changes.
- Using the formula for molarity:
- (H+)=MolesVolume
- Therefore, we have:
- 0.001=0.01V
5. Solve for the final volume V:
- Rearranging the equation gives:
- V=0.010.001=10L
6. Calculate the volume of water to be added:
- Since the initial volume of the solution is 1L, the volume of water to be added is:
- Volume of water=V−Initial Volume=10L−1L=9L
Final Answer:
To achieve a pH of 3, you must add 9 liters of water to the 1 liter of the strong acid solution.
---
- The pH of the initial solution is 2.
- Using the formula pH=−log(H+), we can find the concentration of H⁺ ions.
- (H+)=10−pH=10−2=0.01M
- The volume of the initial solution is 1L.
- Moles of H⁺ ions can be calculated using the formula:
- Moles=Molarity×Volume=0.01mol/L×1L=0.01mol
- The desired pH of the new solution is 3.
- Again using the formula pH=−log(H+):
- (H+)=10−3=0.001M
- Let V be the final volume of the solution after adding water.
- The number of moles of H⁺ ions remains the same (0.01 mol), but the concentration changes.
- Using the formula for molarity:
- (H+)=MolesVolume
- Therefore, we have:
- 0.001=0.01V
- Rearranging the equation gives:
- V=0.010.001=10L
- Since the initial volume of the solution is 1L, the volume of water to be added is:
- Volume of water=V−Initial Volume=10L−1L=9L
To achieve a pH of 3, you must add 9 liters of water to the 1 liter of the strong acid solution.
Topper's Solved these Questions
Similar Questions
How many litres of water must be added to 2 litre aqueous solution of HCI with a pH of 1 to create an aqueous solution with pH of 2 ?
View SolutionIf ammonia is dissolved in water, pH of the solution
View SolutionHow many litres of water must be added to 1L of an aqueous solution of HCl with a pH of 1 to create an aqueous solution with pH of 2?
View SolutionHow many litres of water must be added to 1L of an aqueous solution of HCl with a pH of 1 to create an aqueous solution with pH of 2?
View Solution10 mL of H2A(weak diprotic acid) solution is titrated against 0.1M NaOH. pH of the solution is plotted against volume of strong base added and following observation is made. If pH of the solution at first equivalence point is pH1 and at second equivalence point is pH2. Calculate the value of (pH2−pH1) at 25∘C
Given for H2A,pKa1 =4.6 and pKa2 =8, log 25=1.4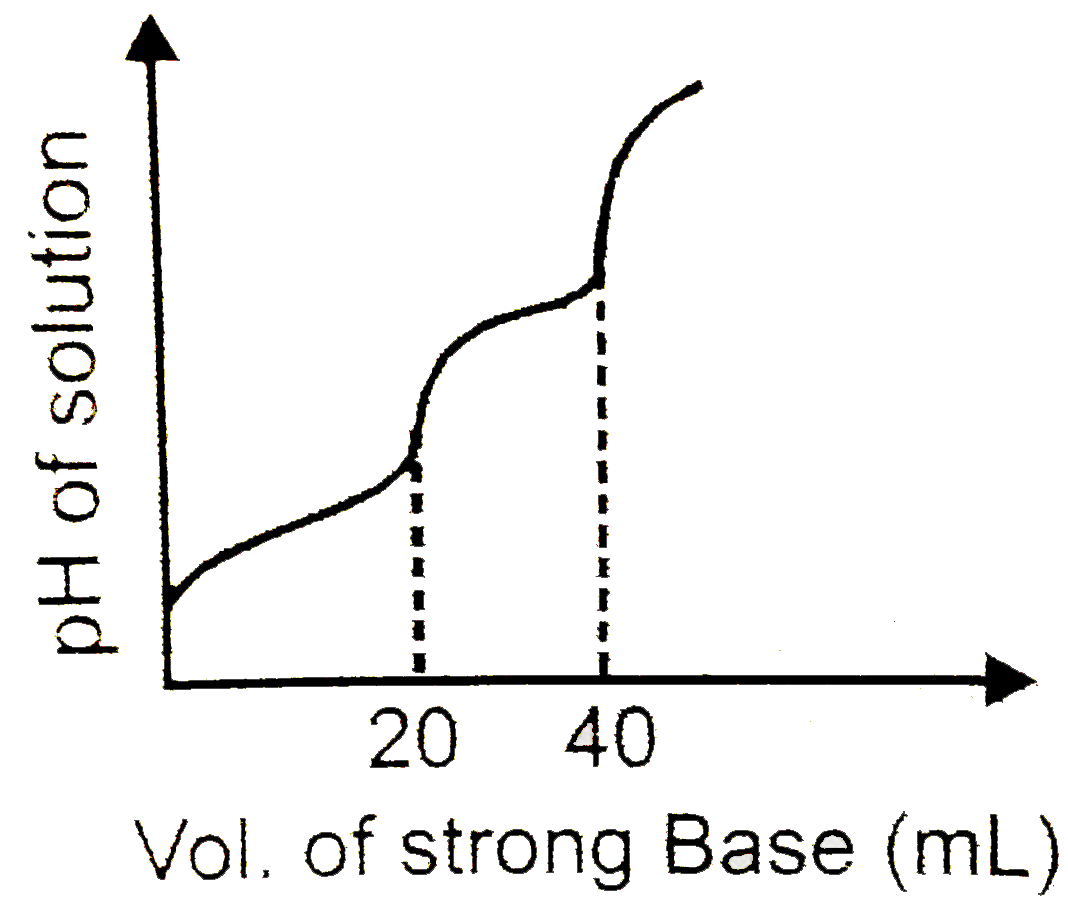
View Solution10 mLof H2A (weak diprotic acid) solutions is titrated against 0.1M NaOH. pH of the solution is plotted against volume of strong base added and following observation is made. If pH of the solution at 1st equivalence point is pH1 and at 2nd equivalence point is pH2, Cal the value (pH2,−pH1) at 25∘C. Given for H2,A,pKal=4.6&pKa2=8

View Solutiona. What amount of H2SO4 must be dissolved in 500mL of solution to have a pH of 2.15?
View Solution10mL of a strong acid solution of pH=2.000 are mixed with 990mL of another strong acid solution of pH=4.000. The pH of the resulting solution will be :
View Solution10 mL of a strong acid solution of pH=2.000 are mixed with 990mL of another strong acid solution of pH=4.000. The pH of the resulting solution will be:
View SolutionWhat is the pH of 1 M solution of acetic acid ? To what volume one litre of this solution be diluted so that pH of the resulting solution will be twice of the original value ? (Ka=1.8×10−5)
View Solution
