The moment of inertia of a flat annular ring having mass M, inner radius a and outer radius b about the diametric axis through the centre is
A. M4(b2+a2)
B. M2(b2+a2)
C. M4(b−a)
D. M4(b2−a2)
To find the moment of inertia of a flat annular ring about the diametric axis through the center, we can follow these steps:
Step 1: Understand the Geometry of the Annular Ring
The annular ring has an inner radius a and an outer radius b. The mass of the ring is M.
Step 2: Divide the Annular Ring into Differential Elements
We can consider the annular ring as being made up of many thin concentric rings. Each thin ring at a distance r from the center with thickness dr has a radius r where a≤r≤b.
Step 3: Find the Mass of the Differential Ring
The area of the differential ring is given by:
dA=2πrdr
The mass of the differential ring can be expressed as:
dm=Mπ(b2−a2)⋅dA=Mπ(b2−a2)⋅2πrdr=2Mrb2−a2dr
Step 4: Calculate the Moment of Inertia of the Differential Ring
The moment of inertia dI of the differential ring about the diametric axis is given by:
dI=r2dm=r2⋅2Mrb2−a2dr=2Mr3b2−a2dr
Step 5: Integrate to Find the Total Moment of Inertia
To find the total moment of inertia I, we integrate dI from r=a to r=b:
I=∫badI=∫ba2Mr3b2−a2dr
Step 6: Perform the Integration
Calculating the integral:
I=2Mb2−a2∫bar3dr
The integral of r3 is:
∫r3dr=r44
Thus,
I=2Mb2−a2(r44)ba=2Mb2−a2(b44−a44)
I=2Mb2−a2⋅b4−a44=M(b4−a4)2(b2−a2)
Step 7: Simplify the Expression
Using the identity b4−a4=(b2−a2)(b2+a2), we can simplify:
I=M(b2+a2)2
Final Result
Thus, the moment of inertia of the flat annular ring about the diametric axis through the center is:
I=M2(b2+a2)
The annular ring has an inner radius a and an outer radius b. The mass of the ring is M.
We can consider the annular ring as being made up of many thin concentric rings. Each thin ring at a distance r from the center with thickness dr has a radius r where a≤r≤b.
The area of the differential ring is given by:
dA=2πrdr
The mass of the differential ring can be expressed as:
dm=Mπ(b2−a2)⋅dA=Mπ(b2−a2)⋅2πrdr=2Mrb2−a2dr
The moment of inertia dI of the differential ring about the diametric axis is given by:
dI=r2dm=r2⋅2Mrb2−a2dr=2Mr3b2−a2dr
To find the total moment of inertia I, we integrate dI from r=a to r=b:
I=∫badI=∫ba2Mr3b2−a2dr
Calculating the integral:
I=2Mb2−a2∫bar3dr
The integral of r3 is:
∫r3dr=r44
Thus,
I=2Mb2−a2(r44)ba=2Mb2−a2(b44−a44)
I=2Mb2−a2⋅b4−a44=M(b4−a4)2(b2−a2)
Using the identity b4−a4=(b2−a2)(b2+a2), we can simplify:
I=M(b2+a2)2
Thus, the moment of inertia of the flat annular ring about the diametric axis through the center is:
I=M2(b2+a2)
Similar Questions
The moment of inertia of a flat angular ring is having mass M, inner radius a and outer radius b about the perpendicular axis through the centre is
View SolutionCalculate the moment of inertia of a ring having mass M, radius Rand having uniform mass distribution about an axis passing through the centre of the ring and perpendicular to the plane of the ring?

View Solution
Knowledge Check
The moment of inertia of a hoop of radius R and mass M, about any tangent
A[3mR2]/2B[mR2]/2CMR2D[MR2]/4
The moment of inertia of a ring of mass M and radius R about PQ axis will be

View SolutionFind the moment of inertia of a uniform ring of mass M and radius R about a diameter.
View SolutionFind the moment of inertia of a pair of spheres, each having a mass m and radius r kept in contact about the tangent passing through the point of contact.
View SolutionFind the moment of inertia of a uniform rectangular plate of mass M and edges of length 'I' and 'b' about its axis passing through the centre and perpendicular to it.
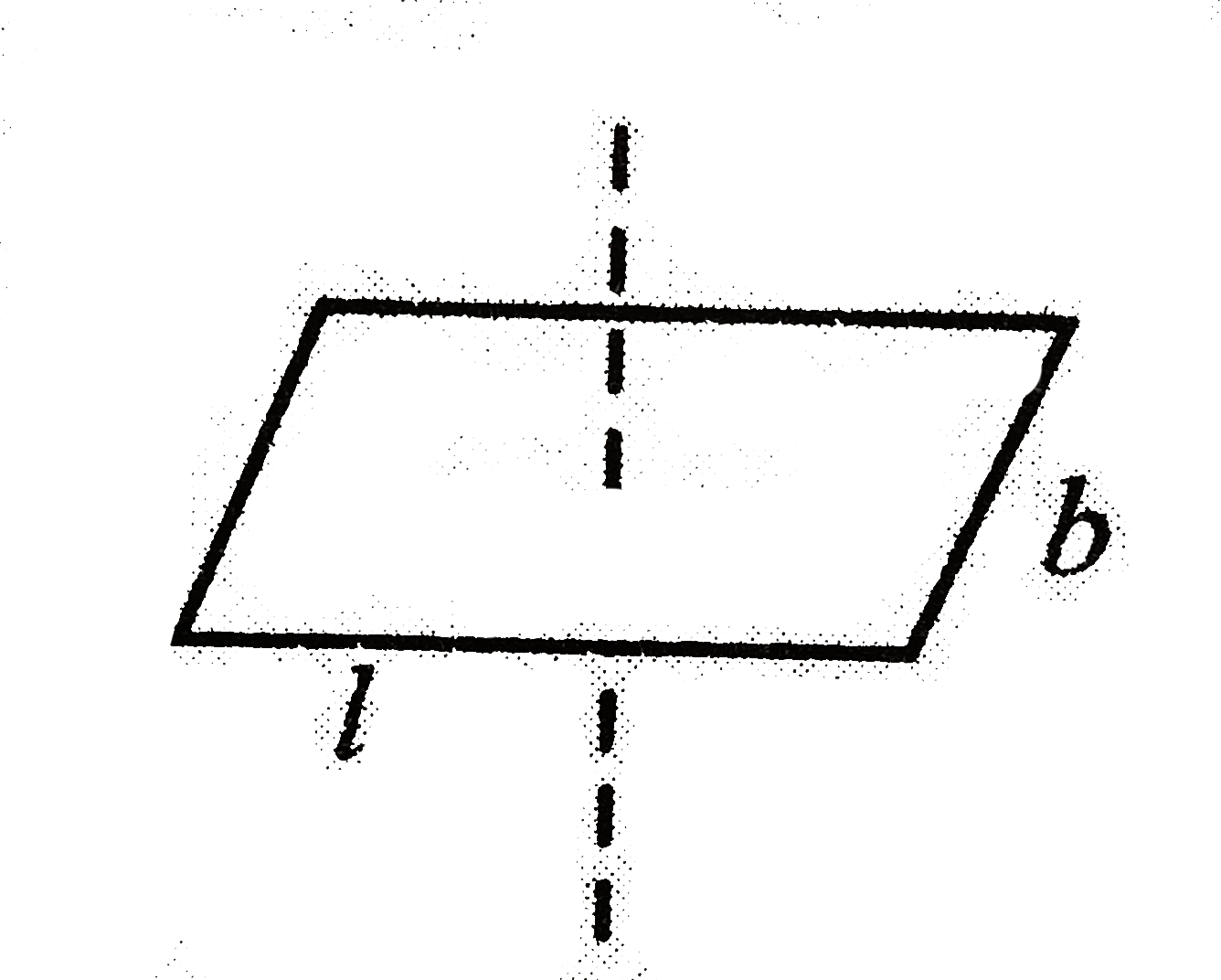
View SolutionLet the moment of inertia of a hollow cylinder of length 30 cm (inner radius 10 cm and outer radius 20 cm ), about its axis be I. the radius of a thin cylinder of the same about its axis is also I is :
View SolutionThe moment of inertia of a uniform semicircularwire of mass M and radius r about a line perpendicular to the plane of the wire through the centre is :
View SolutionThe moment of inertia of a solid cylinder of mass M, length 2R and radius R about an axis passing through the centre of mass and perpendicular to the axis of the cylinder is I1 and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is I2
View Solution
