A particie of mass 10 kg is driven by a machine that delivers a constant power of 20 watts. If particle starts from rest and moves along a straight line, then force (in Newton) on particle at time t(t> 0) is
10√t
10√t
20√t
1√t
To solve the problem, we need to find the force acting on a particle of mass m=10kg that is driven by a machine delivering constant power P=20W. The particle starts from rest and moves along a straight line.
1. Understand the relationship between power, work, and kinetic energy:
P=dWdt
where W is the work done. Since work done is equal to the change in kinetic energy, we can express it as:
W=ΔKE=12mv2−0=12mv2(since it starts from rest)
2. Relate power to work done:
From the power equation, we can write:
dWdt=P⟹dW=Pdt
Integrating both sides gives:
W=Pt
3. Equate the work done to the change in kinetic energy:
Setting the two expressions for work equal gives:
12mv2=Pt
4. Solve for velocity v:
Rearranging the equation:
v2=2Ptm⟹v=√2Ptm
5. Find acceleration a:
Acceleration is the derivative of velocity with respect to time:
a=dvdt=ddt(√2Ptm)
Using the chain rule:
a=12(2Pm)1/2t−1/2=√2Pm⋅12t−1/2
6. Calculate the force F:
The force acting on the particle is given by Newton's second law:
F=ma
Substituting for a:
F=m⋅√2Pm⋅12t−1/2
Simplifying this expression:
F=√2Pm⋅12t−1/2
7. Substituting values:
Now substituting P=20W and m=10kg:
F=√2⋅20⋅10⋅12t−1/2
F=√400⋅12t−1/2=20⋅12t−1/2=10t−1/2
Final Answer:
The force on the particle at time t is:
F=10√tN
P=dWdt
where W is the work done. Since work done is equal to the change in kinetic energy, we can express it as:
W=ΔKE=12mv2−0=12mv2(since it starts from rest)
From the power equation, we can write:
dWdt=P⟹dW=Pdt
Integrating both sides gives:
W=Pt
Setting the two expressions for work equal gives:
12mv2=Pt
Rearranging the equation:
v2=2Ptm⟹v=√2Ptm
Acceleration is the derivative of velocity with respect to time:
a=dvdt=ddt(√2Ptm)
Using the chain rule:
a=12(2Pm)1/2t−1/2=√2Pm⋅12t−1/2
The force acting on the particle is given by Newton's second law:
F=ma
Substituting for a:
F=m⋅√2Pm⋅12t−1/2
Simplifying this expression:
F=√2Pm⋅12t−1/2
Now substituting P=20W and m=10kg:
F=√2⋅20⋅10⋅12t−1/2
F=√400⋅12t−1/2=20⋅12t−1/2=10t−1/2
The force on the particle at time t is:
F=10√tN
Similar Questions
A particle of mass m is driven by a machine that delivers a constant power k watts. If the particle starts from rest the force on the particle at time t is
View SolutionA partical of mass m is driven by a machine that deleveres a constant power k watts. If the partical starts from rest the force on the partical at time t is
View SolutionA body of mass 2 kg is driven by an engine delivering a constant power of 1 J /s. The body starts from rest and moves in a straight line. After 9 seconds, the body has moved a distance ( in m) ……….. .
View SolutionA particle is moving with a constant speed along a straight line path. A force is not required to
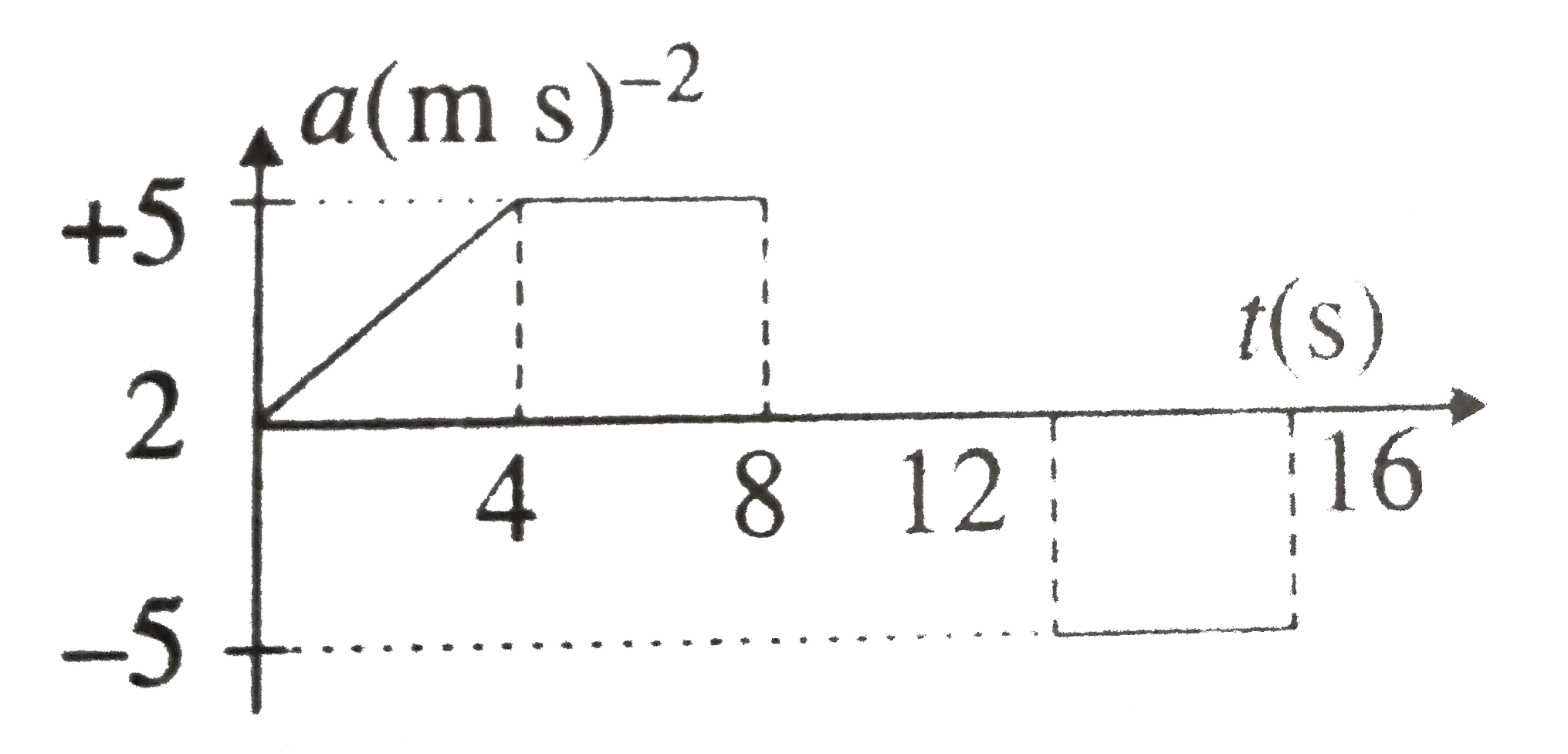
View SolutionThe acceleration of a particle starting from rest and travelling along a straight line is shown in figure. The maximum speed of the particle is
View SolutionA particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is

View SolutionA particle starts motion from rest and moves along a straight line. Its velocity-time graph is shown. Find out speed of particle at t=2s and at t=3s.

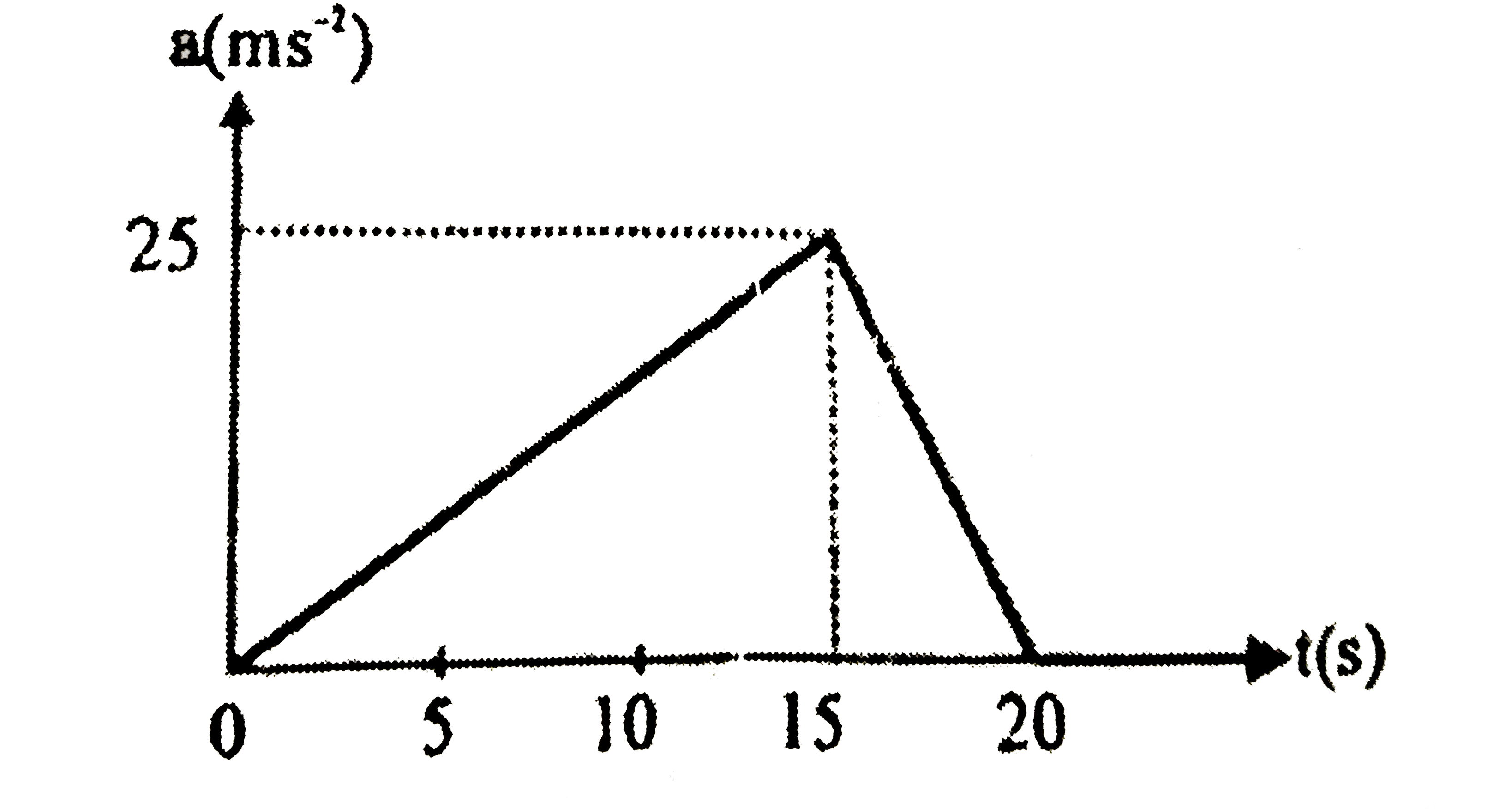
View SolutionFigure shows acceleration versus time graph of a particle starting from rest and moving along a straight line. Which of the following staement (s) is/are correct ?
View SolutionA particle starts motion from rest and moves along a straight line. Its acceleration-time graph is shown. Find out speed of particle at t=2s and at t=3s.

View SolutionA particle of mass 0.2kg is moving in one dimension under a force that delivers constant power 0.5W to the particle.If the initial speed =0 then the final speed (in ms−1) after 5s is.
View Solution