A uniform linear thermometer scale is at steady state with its 0 cm mark at −10°C and 50cm mark at 80°C . temperature corresponding to 70cm marks is
126°C
136°C
106°C
116°C
To solve the problem, we need to find the temperature corresponding to the 70 cm mark on a linear thermometer scale, where the 0 cm mark corresponds to -10°C and the 50 cm mark corresponds to 80°C.
1. Identify the Known Points:
- At 0 cm, the temperature is -10°C.
- At 50 cm, the temperature is 80°C.
2. Determine the Change in Temperature and Length:
- The change in temperature from -10°C to 80°C is:
ΔT=80−(−10)=80+10=90°C
- The change in length from 0 cm to 50 cm is:
ΔL=50−0=50 cm
3. Calculate the Slope (Rate of Change of Temperature with Respect to Length):
- The slope (m) of the linear relationship is given by:
m=ΔTΔL=90°C50 cm=95 °C/cm
4. Set Up the Equation for the Temperature at 70 cm:
- Let y be the temperature at 70 cm. The change in length from 0 cm to 70 cm is:
ΔL′=70−0=70 cm
- Using the linear relationship, we can express the temperature at 70 cm as:
y−(−10)=m⋅ΔL′
- Substituting the values:
y+10=95⋅70
5. Calculate the Temperature:
- First, calculate 95⋅70:
95⋅70=9⋅14=126
- Now, substitute back to find y:
y+10=126
y=126−10=116°C
6. Final Answer:
- The temperature corresponding to the 70 cm mark is 116°C.
- At 0 cm, the temperature is -10°C.
- At 50 cm, the temperature is 80°C.
- The change in temperature from -10°C to 80°C is:
ΔT=80−(−10)=80+10=90°C
- The change in length from 0 cm to 50 cm is:
ΔL=50−0=50 cm
- The slope (m) of the linear relationship is given by:
m=ΔTΔL=90°C50 cm=95 °C/cm
- Let y be the temperature at 70 cm. The change in length from 0 cm to 70 cm is:
ΔL′=70−0=70 cm
- Using the linear relationship, we can express the temperature at 70 cm as:
y−(−10)=m⋅ΔL′
- Substituting the values:
y+10=95⋅70
- First, calculate 95⋅70:
95⋅70=9⋅14=126
- Now, substitute back to find y:
y+10=126
y=126−10=116°C
- The temperature corresponding to the 70 cm mark is 116°C.
Similar Questions
A uniform thermometre scale is at steady state with its 0 cm mark at 20°C and 100 cm mark at 100°C. Temperature of the 60 cm mark is-
View SolutionA uniform metre scale can be balanced at the 70.0 cm mark when a mass of 0.05 kg is hung from the 94.0 cm mark.
Find the mass of the metre scale.
View Solution
Knowledge Check
Find the weight of a metre scale balanced at 30cm mark such that two weights one of 30gf and 10gf are suspended at 5cm mark and 40cm mark respectively.
A10gfB105gfC25gfD32.5gf
A uniform metre rod is balanced at the 70 cm mark by suspending a weight of 50 gf at the 40 cm mark and 200 gf at the 95 cm mark. Draw a diagram of the arrangement and calculate the weight of the metre rod.
View SolutionA uniform metre scale can be balanced at the 70.0 cm mark when a mass of 0.05 kg is hung from the 94.0 cm mark.
Draw a diagram of the arrangement.
View SolutionA constant volume gas thermometer shows pressure readings of 60 cm and 90 cm of mercury at 0∘C and 100∘C respectively. What is the temperature on gas scale, when pressure reading is 70 cm of mercury?
View SolutionA constant volume gas thermometer show pressure reading of 50cm and 99 cm of mercury at 0∘C and 100∘C respectively. When the pressure reading is 60 cm of mercury, the temperature is
View SolutionA constant volume gas thermometer shows pressure reading of 50 cm and 90 cm of mercury at 0∘C and 100∘C respectively. When the pressure reading is 60 cm of mercury, the temperature is:
View SolutionA uniform meter scale is kept in equilibrium when supported at the 60 cm mark and a mass weight of the scale is greater than, less than or equal to the weight of mass M.
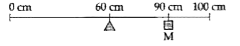
View SolutionThe readings of a thermometer at 0∘C and 100∘C are 50cm and 75cm of mercury column respectively. Find the temperature at which its reading is 80cm of mercury column ?
View Solution
