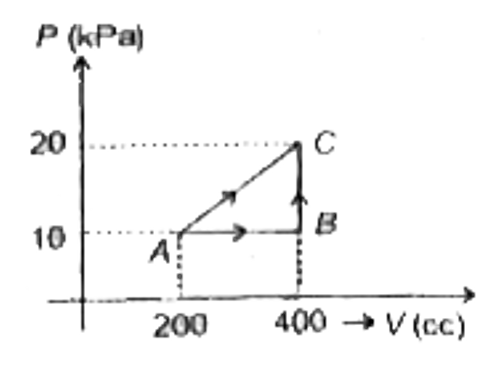
the volume( V) of a polyatomic( non linear molecule) gas varies with its temperature(T) , as shown in figure. The ratio of the heat absorbed by the gas to the work done by the gas, when gas is taken from state A to state B , is ( neglect vibrational mode)
_PHY_E05_037_Q01.png)
5:2
3:2
7:2
4:1
Step by step video & image solution for the volume( V) of a polyatomic( non linear molecule) gas varies with its temperature(T) , as shown in figure. The ratio of the heat absorbed by the gas to the work done by the gas, when gas is taken from state A to state B , is ( neglect vibrational mode) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
The ednsity (ρ) of an ideal gas varies with temperature T as shown in figure. Then

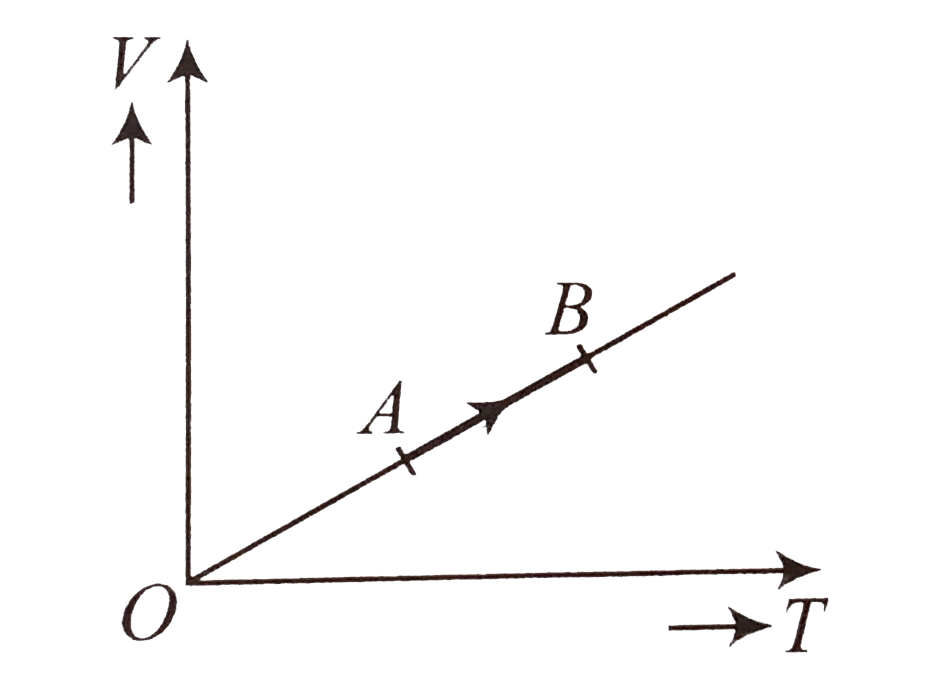
View SolutionThe volume (V) of a monatomic gas varies with its temperature (T) as shown in the graph. The ratio of work done by the gas, to the heat absorbed by it, when it undergoes a change from state A to state B,is
View SolutionVolume versus temperature graph of two moles of helium gas is as shown in figure. The ratio of heat absorbed and the work done by the gas in process 1−2 is
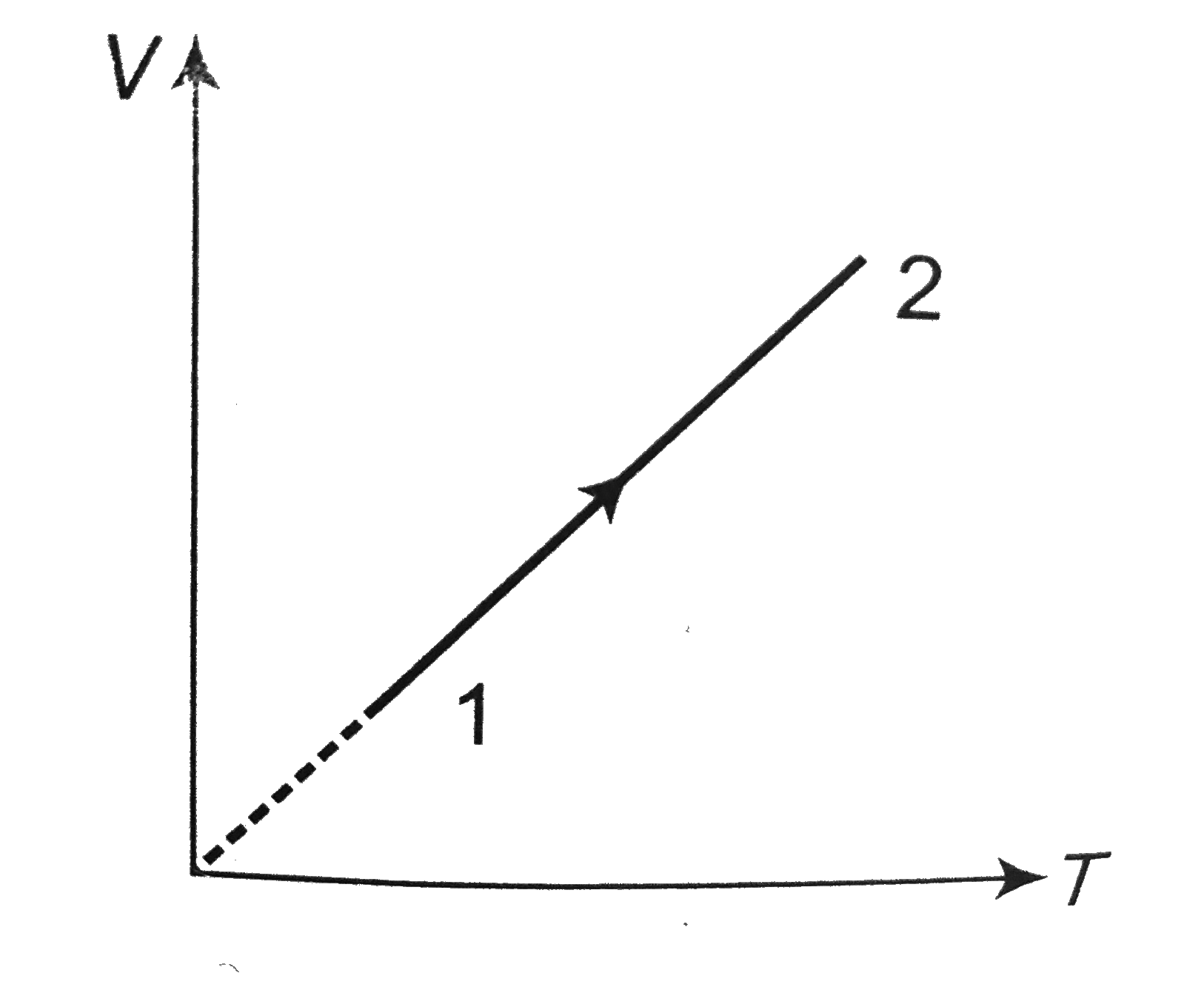
View SolutionVolume versus temperature graph of two moles of helium gas is as shown in figure. The ratio of heat absorbed and the work done by the gas in process 1−2 is

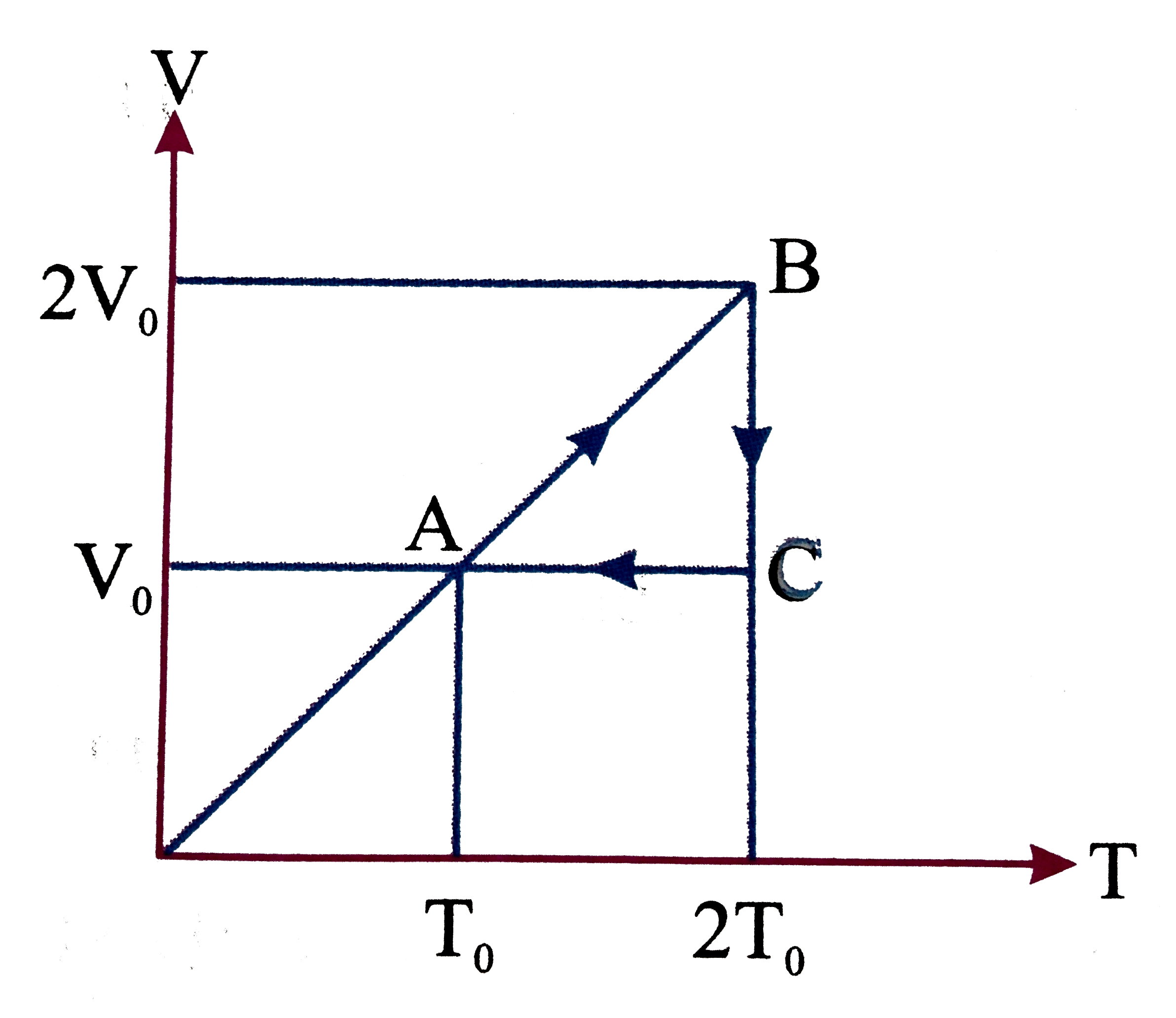
View SolutionAn ideal monoatomic gas undergoes a cyclic process ABCA as shown in the figure. The ratio of heat absorbed during AB to the work done on the gas during BC id
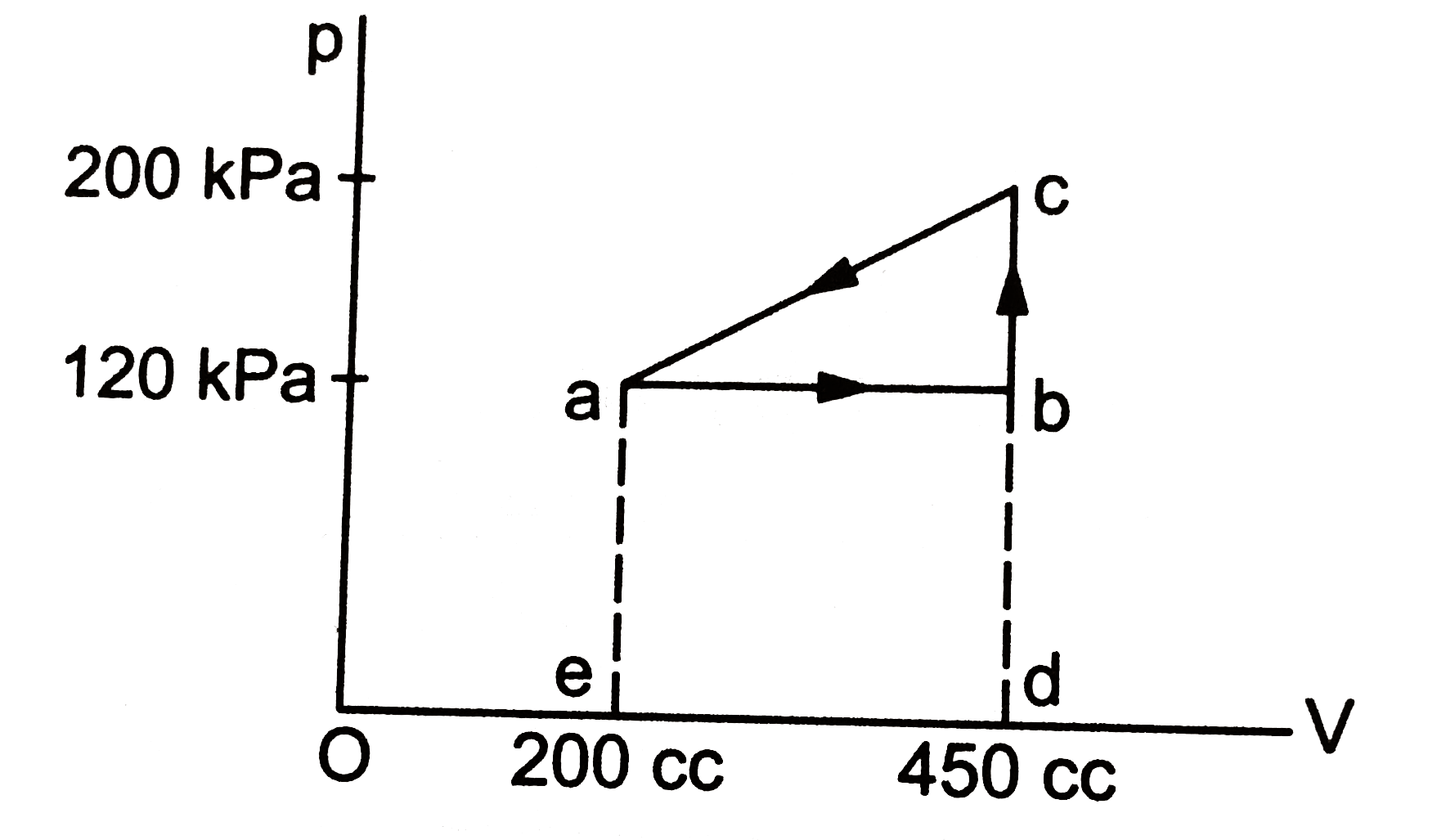
View Solutioncalculate the work done by a gas as it is taken from the state a to b, b to c and c to a as shown in
View SolutionCalculate the work done by the gas in the state diagram shown :

View SolutionIf a gas is taken from A to C through B then heat absorbed by the gas 8 J . Heat absorbed by the gas in taking it from A to C directly is
View SolutionAn ideal gas goes from the state i to the state ∫ as shown in .the work done by the gas during the process

View SolutionThe pressure P of an ideal diatomic gas varies with its absolute temperature T as shown in figure . The molar heat capacity of gas during this process is [R is gas constant]
View Solution
