A wire of resistance(3Ω) per meter is bent to from a regular hexagon of side 2 m. The resistance between points A and B as shown in figure is
(12Ω)
(8Ω)
(4Ω)
(24Ω)
To find the resistance between points A and B in a regular hexagon formed by a wire of resistance 3Ω per meter and side length 2m, we can follow these steps:
Step 1: Calculate the resistance of each side of the hexagon
The resistance per meter of the wire is 3Ω. Since each side of the hexagon is 2m, the resistance of each side can be calculated as follows:
Rside=Resistance per meter×Length of side=3Ω/m×2m=6Ω
Step 2: Identify the configuration of resistances
In a regular hexagon, when we look at points A and B, we can see that there are three sides connecting A to B directly and three sides that are not directly connecting A to B. The three sides directly connecting A and B are in series, and the remaining three sides are also in series.
Step 3: Calculate the total resistance of the three sides connecting A and B
Since the three sides connecting A and B are in series, their total resistance can be calculated as:
RAB=Rside+Rside+Rside=6Ω+6Ω+6Ω=18Ω
Step 4: Calculate the total resistance of the three sides not connecting A and B
Similarly, the total resistance of the three sides that are not directly connecting A and B is also:
RnotAB=Rside+Rside+Rside=6Ω+6Ω+6Ω=18Ω
Step 5: Combine the two sets of resistances in parallel
Now, we have two resistances of 18Ω each (one from A to B and one from the other sides). Since these two resistances are in parallel, we can use the formula for parallel resistances:
1Req=1RAB+1RnotAB=118+118
Calculating this gives:
1Req=218=19
Thus, the equivalent resistance Req is:
Req=9Ω
Final Answer:
The resistance between points A and B is 9Ω.
---
The resistance per meter of the wire is 3Ω. Since each side of the hexagon is 2m, the resistance of each side can be calculated as follows:
In a regular hexagon, when we look at points A and B, we can see that there are three sides connecting A to B directly and three sides that are not directly connecting A to B. The three sides directly connecting A and B are in series, and the remaining three sides are also in series.
Since the three sides connecting A and B are in series, their total resistance can be calculated as:
Similarly, the total resistance of the three sides that are not directly connecting A and B is also:
Now, we have two resistances of 18Ω each (one from A to B and one from the other sides). Since these two resistances are in parallel, we can use the formula for parallel resistances:
The resistance between points A and B is 9Ω.
Similar Questions
The equivalent resistance between points A and B in the circuit shown in figure is
_PHY_E05_095_Q01.png)
View SolutionThe equivalent resistance between point A and B in the circuit shown in figure is
_PHY_E05_041_Q01.png)
View SolutionA wire of resistance 20Ω is bent to form a complete circle. The resistance between two diametrically opposite points A and B as shown in the figure, is
View SolutionA wire of resistance 15.0(Ω)is bent to form a regular hexagon ABCDEFA.Find the equivalent resistance of the loop between the points (a)A and B, (b)A and C and (c )A and D .
View SolutionA wire of resistance 15.0(Ω)is bent to form a regular hexagon ABCDEFA.Find the equivalent resistance of the loop between the points (a)A and B, (b)A and C and (c )A and D .
View SolutionThe equivalen resistance between A and B in the network shown in figure is
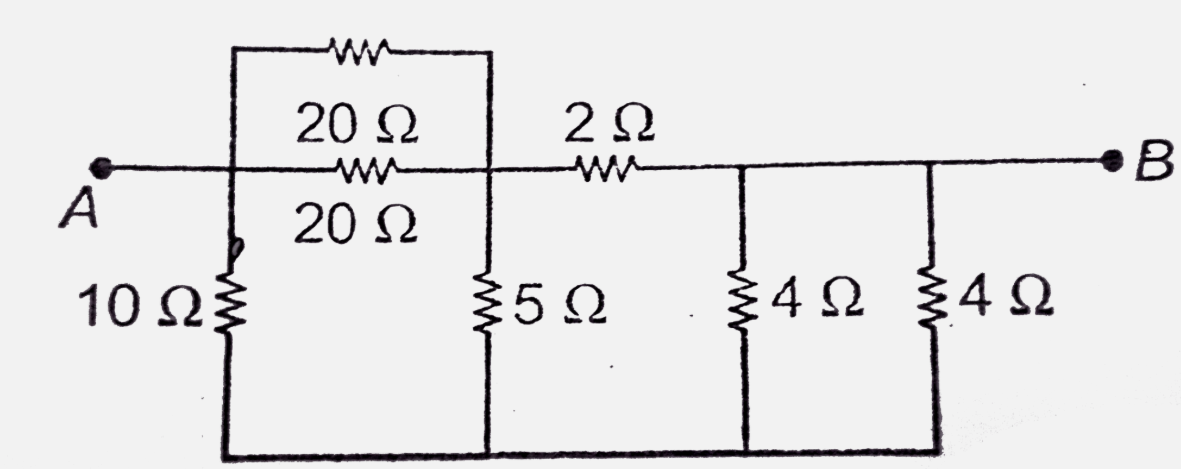
View SolutionFind the effective resistance between points A and B for the network shown in the figure below.
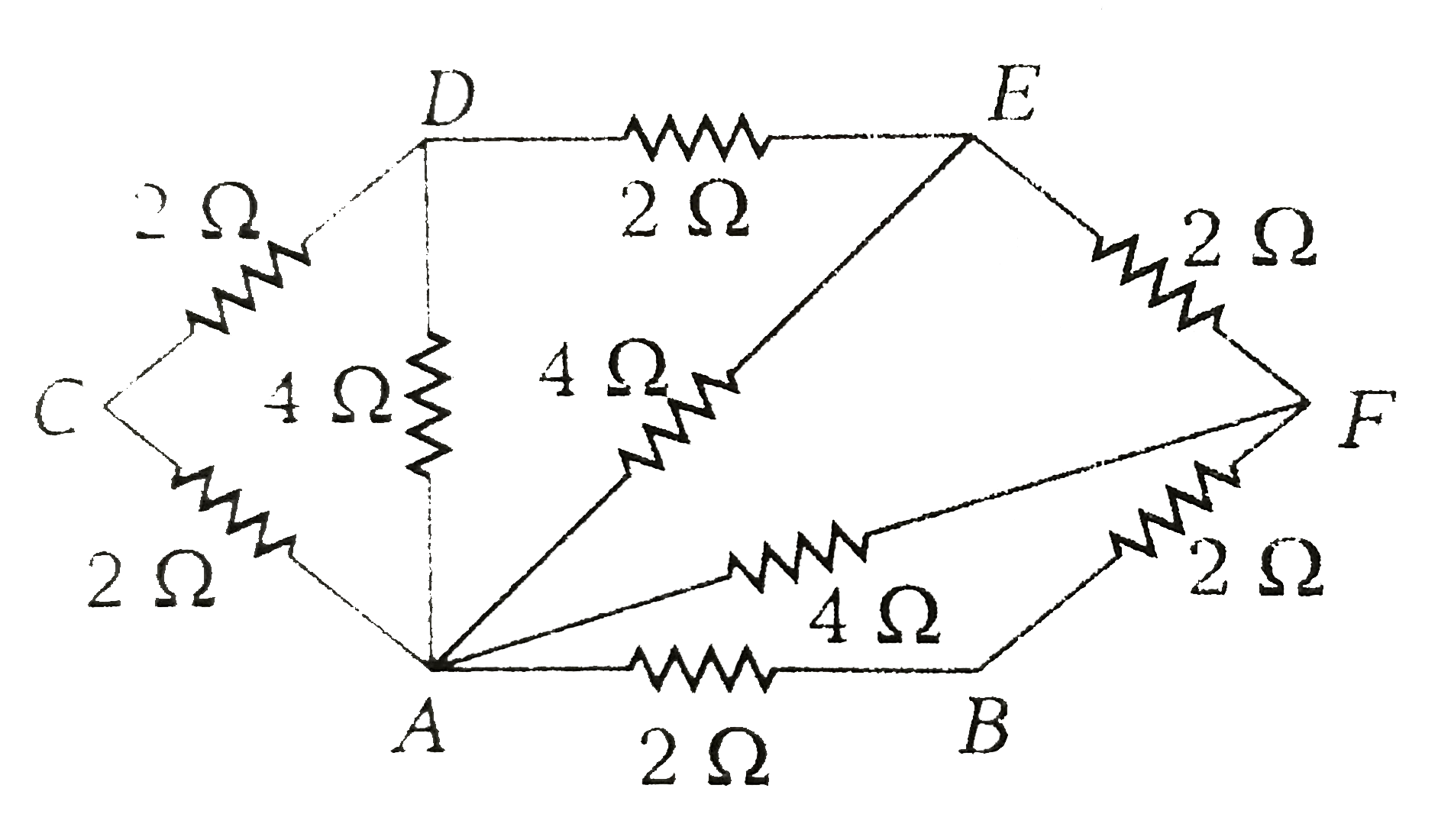
View SolutionThe equivalent resistance resistance between A and B of network shown in figure is
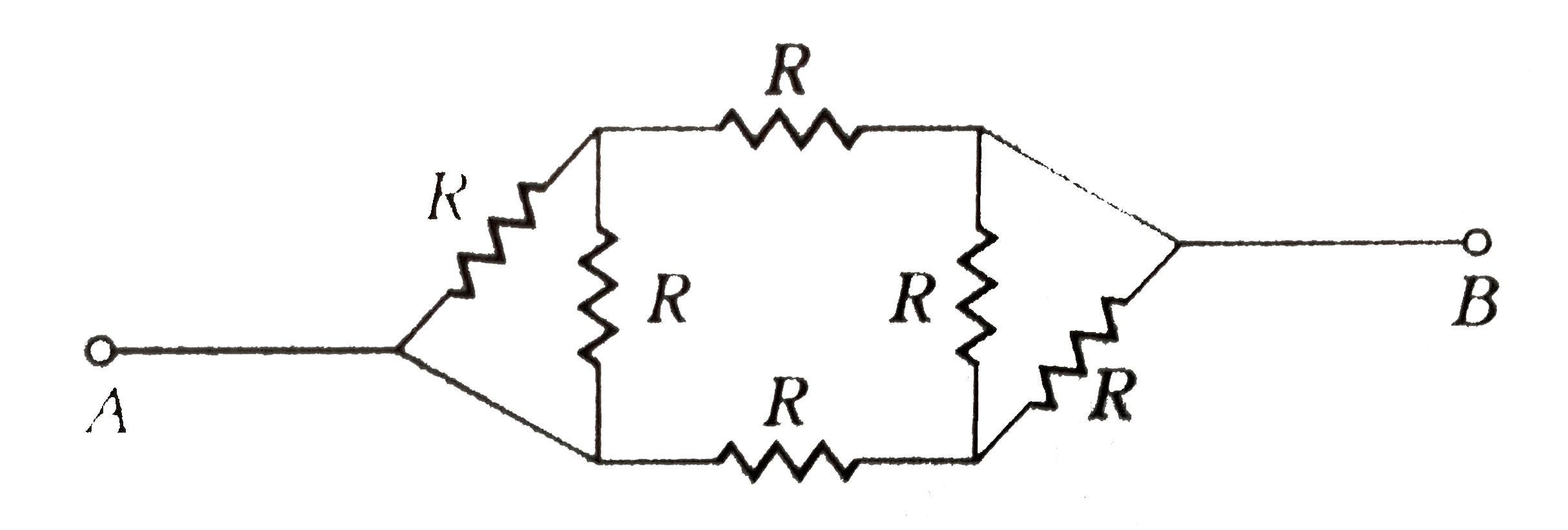
View SolutionEquivalent resistance between the points A and B (in Ω)
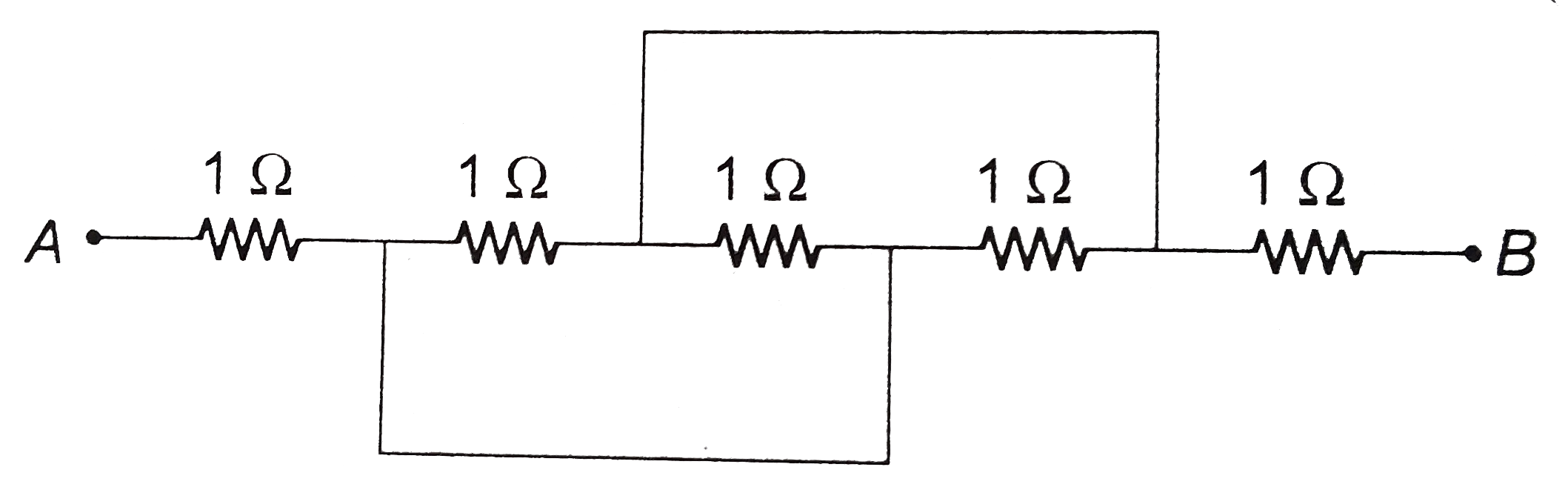 .
.
View SolutionA wire of resistance 12Ωm−1 is bent to from a complete circle of radius 10cm. The resistance between its two diametrically opposite points, A and B as shown in the figure, is
View Solution
