A boy weighing 250 N slides down upto the ground from the top of a slide. The friction offered by the slide is three tenth of his weight. The length and height of the slide is 10 m and 8 m, respectively. The work done by the slide on the boy as he comes down to the ground is
−1250 J
2000 J
−750 J
750 J
To solve the problem, we need to calculate the work done by the slide on the boy as he slides down. Here are the steps to find the solution:
Step 1: Identify the Weight of the Boy
The weight of the boy is given as:
W=250N
Step 2: Calculate the Frictional Force
The frictional force (F_friction) is given as three-tenths of the boy's weight:
Ffriction=310×W
Ffriction=310×250
Ffriction=75N
Step 3: Determine the Length of the Slide
The length of the slide (s) is given as:
s=10m
Step 4: Calculate the Work Done by the Slide
The work done (W_slide) by the slide on the boy is calculated using the formula:
Wslide=Ffriction×s×cos(θ)
Since the frictional force acts in the opposite direction to the displacement, the angle (θ) between the frictional force and the displacement is 180 degrees. Therefore, cos(180∘)=−1:
Wslide=Ffriction×s×(−1)
Wslide=75×10×(−1)
Wslide=−750J
Final Answer
The work done by the slide on the boy as he comes down to the ground is:
Wslide=−750J
The weight of the boy is given as:
W=250N
The frictional force (F_friction) is given as three-tenths of the boy's weight:
Ffriction=310×W
Ffriction=310×250
Ffriction=75N
The length of the slide (s) is given as:
s=10m
The work done (W_slide) by the slide on the boy is calculated using the formula:
Wslide=Ffriction×s×cos(θ)
Since the frictional force acts in the opposite direction to the displacement, the angle (θ) between the frictional force and the displacement is 180 degrees. Therefore, cos(180∘)=−1:
Wslide=Ffriction×s×(−1)
Wslide=75×10×(−1)
Wslide=−750J
The work done by the slide on the boy as he comes down to the ground is:
Wslide=−750J
Similar Questions
In a children\'s park, there is a slide which has a total length of 10 m and a height of 8.0 m figure. Vertical ladder are provided to reach the top. A boy weighting 200 N climbs up the ladder to the top of the slide and slides down to the ground. The averages friction offered by the slide is three tenth of his weight. Find a. the work done by the ladder on the boy as he goes up. b. the work done by the slide on the boy as he comes down. Neglect any work done by forces inside the body of the boy.
View SolutionIn a children\'s park, there is a slide which has a total length of 10 m and a height of 8.0 m figure. Vertical ladder are provided to reach the top. A boy weighting 200 N climbs up the ladder to the top of the slide and slides down to the ground. The averages friction offered by the slide is three tenth of his weight. Find a. the work done by the ladder on the boy as he goes up. b. the work done by the slide on the boy as he comes down. Neglect any work done by forces inside the body of the boy.
View SolutionA block of ice starts sliding down from the top of an inclined roof of a along a line of the greatest slope. The inclination of the roof with the horizontal is 30∘. The heights of the highest and lowerst points of the roof are 8.1 m and 5.6 m respectively.At what horizontal distance from the lowest point will the block hit the ground ? Neglect air friction .[g=9.8m/s2].
View SolutionA boy of weight 25kg slides down a rope hanging from the branch of a tree. If the force of friction against him is 50N, the boy's acceleration is (g=10ms−2)
View SolutionA child weighing 25 kg slides down a rope hanging from a branch of a tall tree. If the force of friction acting against him is 200 N, the acceleration of child is (g=10m/s2)
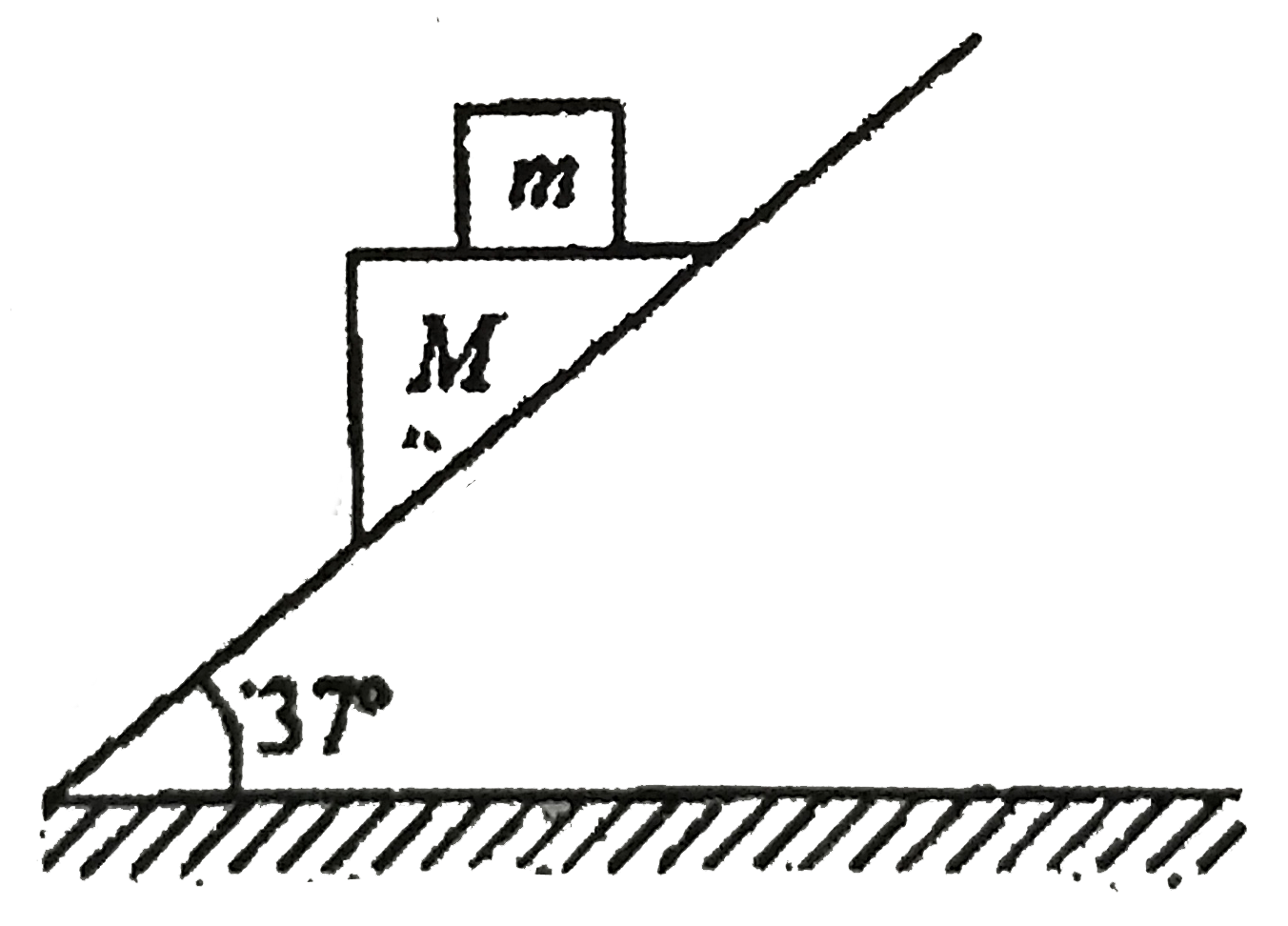
View SolutionBlock M slides down on frictionless incline as shown. The minimum friction coefficient so that m does not slide with respect to M would be :
View SolutionA block of mass 10 kg slides down on an incline 5 m long and 3 m high. A man pushes up on the ice block parallel to the incline so that it slides down at constant speed. The coefficient of friction between the ice and the incline is 0.1. Find :
(a) the work done by the man on the block.
(b) the work done by gravity on the block.
(c) the work done by the surface on the block.
(d) the work done by the resultant forces on the block.
(e) the change in K.E. of the block.
View SolutionA small body of mass m slides without friction from the top of a hemisphere of radius r. At what hight will the body be detached from the surface of hemisphere?

View SolutionA block of mass m slides down along the surface of the bowl from the rim to the bottom as shown in fig. The velocity of the block at the bottom will be-

View SolutionIn the figure shown, a solid sphere of mass 'm' and radius r is released from a height 6r to slide down a smooth surface. A plank of same mass 'm' touches the horizontal portion of the surface at the ground. The co-efficient of friction between the plank and the sphere is μ and that between the plank and the ground is μ/4. Find the work done by the friction force between the plank and the ground till the sphere starts pure rolling on the plank. Neglect the height of the plank.

View Solution
