The direction of the magnetic force on a positive charge q moving with velocity v in a uniform magnetic field B for the following cases.
(i) magnetic field is out of the plane of paper and velocity vector is eastward (ii) magnetic field is directed South ward and velocity vector is in south west direction.
In case (i) force is southward. In case (ii) force is directed into the plane of paper
In case (i) force is Southward. In case (ii) force is eastward.
In case (i) force is Southward. In case (ii) force is directed out of the plane of paper.
In case (i) force is northward. In case (ii) force is directed out of the plane of paper.
To determine the direction of the magnetic force on a positive charge q moving with velocity v in a uniform magnetic field B, we can use the right-hand rule and the formula for the magnetic force:
F=qv×B
Let's analyze each case step by step.
Case (i): Magnetic field is out of the plane of paper, and velocity vector is eastward.
1. Identify the vectors:
- The magnetic field B is out of the plane of the paper, which we can represent as B=k^ez (where k is a positive constant).
- The velocity vector v is eastward, which we can represent as v=v^ex (where v is a positive constant).
2. Apply the cross product:
- We need to calculate F=qv×B.
- Substituting the vectors, we have:
F=q(v^ex)×(k^ez)
3. Calculate the cross product:
- Using the right-hand rule or the determinant method:
^ex×^ez=^ey
- Therefore:
F=qvk^ey
- Since q and k are positive, the force direction is in the positive ^ey direction, which is southward.
Conclusion for Case (i):
The magnetic force is directed southward.
---
Case (ii): Magnetic field is directed southward, and velocity vector is in the southwest direction.
1. Identify the vectors:
- The magnetic field B is directed southward, which we can represent as B=−j^ey.
- The velocity vector v is in the southwest direction. This can be represented as:
v=v(−^ex−^ey)=−v^ex−v^ey
2. Apply the cross product:
- We need to calculate F=qv×B.
- Substituting the vectors:
F=q(−v^ex−v^ey)×(−^ey)
3. Calculate the cross product:
- Distributing the cross product:
F=q(v^ex×^ey+v^ey×^ey)
- Since ^ey×^ey=0:
F=qv^ex×^ey
- Using the right-hand rule:
^ex×^ey=^ez
- Therefore:
F=qv^ez
- Since q and v are positive, the force direction is out of the plane of the paper.
Conclusion for Case (ii):
The magnetic force is directed out of the plane of the paper.
---
Summary of Results:
- For Case (i): The force is southward.
- For Case (ii): The force is out of the plane of the paper.
- The magnetic field B is out of the plane of the paper, which we can represent as B=k^ez (where k is a positive constant).
- The velocity vector v is eastward, which we can represent as v=v^ex (where v is a positive constant).
- We need to calculate F=qv×B.
- Substituting the vectors, we have:
F=q(v^ex)×(k^ez)
- Using the right-hand rule or the determinant method:
^ex×^ez=^ey
- Therefore:
F=qvk^ey
- Since q and k are positive, the force direction is in the positive ^ey direction, which is southward.
The magnetic force is directed southward.
- The magnetic field B is directed southward, which we can represent as B=−j^ey.
- The velocity vector v is in the southwest direction. This can be represented as:
v=v(−^ex−^ey)=−v^ex−v^ey
- We need to calculate F=qv×B.
- Substituting the vectors:
F=q(−v^ex−v^ey)×(−^ey)
- Distributing the cross product:
F=q(v^ex×^ey+v^ey×^ey)
- Since ^ey×^ey=0:
F=qv^ex×^ey
- Using the right-hand rule:
^ex×^ey=^ez
- Therefore:
F=qv^ez
- Since q and v are positive, the force direction is out of the plane of the paper.
The magnetic force is directed out of the plane of the paper.
- For Case (i): The force is southward.
- For Case (ii): The force is out of the plane of the paper.
Similar Questions
Knowledge Check
A charged particle is moving on circular path with velocityv in a uniform magnetic field B, if the velocity of the charged particle is doubled and strength of magnetic field is halved, then radius becomes
A8 timesB4 timesC2 timesD16 times
Direction of magnetic field at equatorial point
View SolutionDefine one tesla using the expression fo the magnetic force acting on a particle of charge .q. moving with velocity →v in a magnetic field →B.
View SolutionA small conducting rod of length l, moves with a uniform velocity v in a uniform magnetic field B as shown in fig __

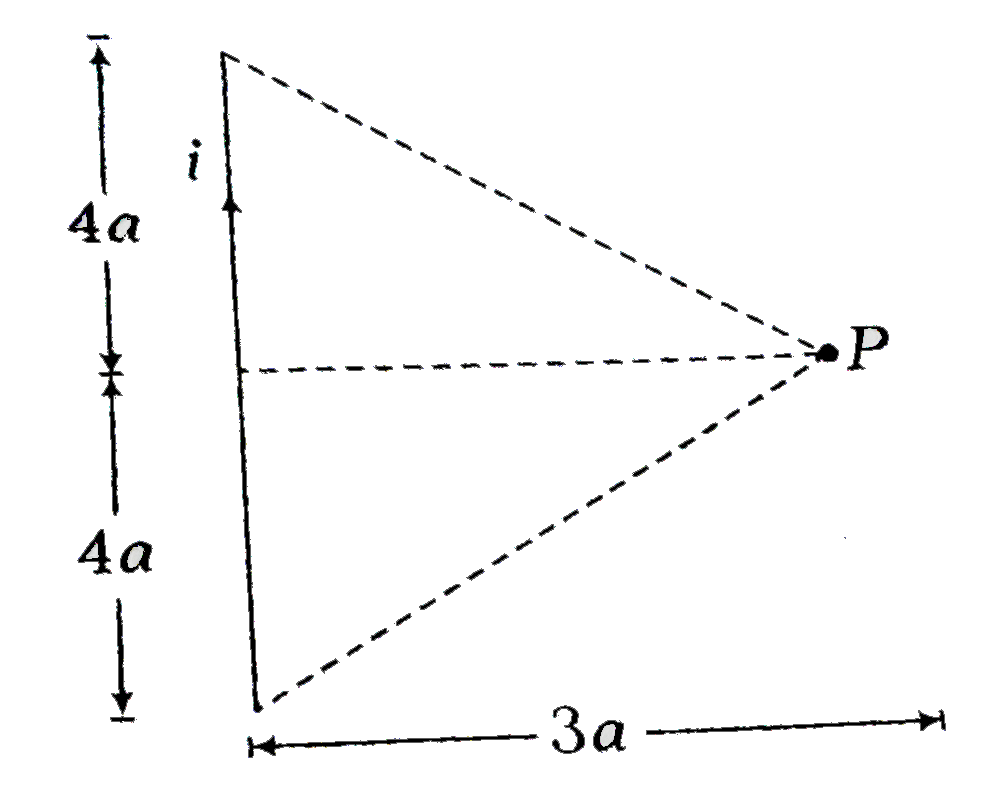
View SolutionEvaluate magnitude and direction of magnetic field at a point P in the following cases

View SolutionWrite an expression in a vector form for the Lorentz magnetic force →F on a charge Q moving with velocity →V in a magnetic field →B. What is the direction of the magnetic force?
View SolutionWrite the expression for Lorentz magnetic force on a particle of charges 'q' moving with velocity →v in a magnetic field →B.
View SolutionFind the magnitude and direction of magnetic field at point O in the following case

View Solution
