If current ,(where K is a constant and t is time) then RMS value of current for one complete cycle is
Zero
To find the RMS (Root Mean Square) value of the current given by I=Kcos(ωt), we can follow these steps:
1. Understand the Definition of RMS Current:
The RMS value of an alternating current is defined as the value of direct current (DC) that would produce the same amount of heat in a resistor over the same period of time.
2. Write the Expression for Heat Generated:
The heat generated by a current I over a time t in a resistor R is given by:
dH=I2Rdt
For one complete cycle, we will integrate this expression over the period T.
3. Substitute the Current Expression:
Substitute I=Kcos(ωt) into the heat equation:
dH=(Kcos(ωt))2Rdt=K2cos2(ωt)Rdt
4. Integrate Over One Complete Cycle:
The total heat H generated over one complete cycle (from t=0 to t=T) is:
H=∫T0K2cos2(ωt)Rdt
Factor out constants:
H=K2R∫T0cos2(ωt)dt
5. Use the Identity for Cosine Squared:
We can use the identity:
cos2(θ)=1+cos(2θ)2
Applying this, we get:
H=K2R∫T01+cos(2ωt)2dt
6. Evaluate the Integral:
The integral can be split:
H=K2R(12∫T0dt+12∫T0cos(2ωt)dt)
The first integral evaluates to T2, and the second integral evaluates to zero over one complete cycle:
H=K2R(12T+0)=K2RT2
7. Calculate the Heat for DC Current:
For DC current IDC, the heat generated over the same time T is:
HDC=I2DCRT
8. Equate the Two Heat Expressions:
Set the heat generated by AC equal to that of DC:
K2RT2=I2DCRT
Cancel RT (assuming R and T are non-zero):
K22=I2DC
9. Solve for the RMS Current:
Taking the square root gives us the RMS value:
IRMS=K√2
Final Answer:
The RMS value of the current for one complete cycle is:
IRMS=K√2
The RMS value of an alternating current is defined as the value of direct current (DC) that would produce the same amount of heat in a resistor over the same period of time.
The heat generated by a current I over a time t in a resistor R is given by:
dH=I2Rdt
For one complete cycle, we will integrate this expression over the period T.
Substitute I=Kcos(ωt) into the heat equation:
dH=(Kcos(ωt))2Rdt=K2cos2(ωt)Rdt
The total heat H generated over one complete cycle (from t=0 to t=T) is:
H=∫T0K2cos2(ωt)Rdt
Factor out constants:
H=K2R∫T0cos2(ωt)dt
We can use the identity:
cos2(θ)=1+cos(2θ)2
Applying this, we get:
H=K2R∫T01+cos(2ωt)2dt
The integral can be split:
H=K2R(12∫T0dt+12∫T0cos(2ωt)dt)
The first integral evaluates to T2, and the second integral evaluates to zero over one complete cycle:
H=K2R(12T+0)=K2RT2
For DC current IDC, the heat generated over the same time T is:
HDC=I2DCRT
Set the heat generated by AC equal to that of DC:
K2RT2=I2DCRT
Cancel RT (assuming R and T are non-zero):
K22=I2DC
Taking the square root gives us the RMS value:
IRMS=K√2
The RMS value of the current for one complete cycle is:
IRMS=K√2
Similar Questions
If currentI=Kcosωt+Ksinωt, (where K is a constant and t is time), then RMS value of current for one complete cycle is
View SolutionIn Fig, the mutual inductance of a coil and a very long straight wire is M, coil has resistance R and self-inductance L. The current in the wire varies according to the law I=at, where a is a constant and t is the time, the time dependence of current in the coil is
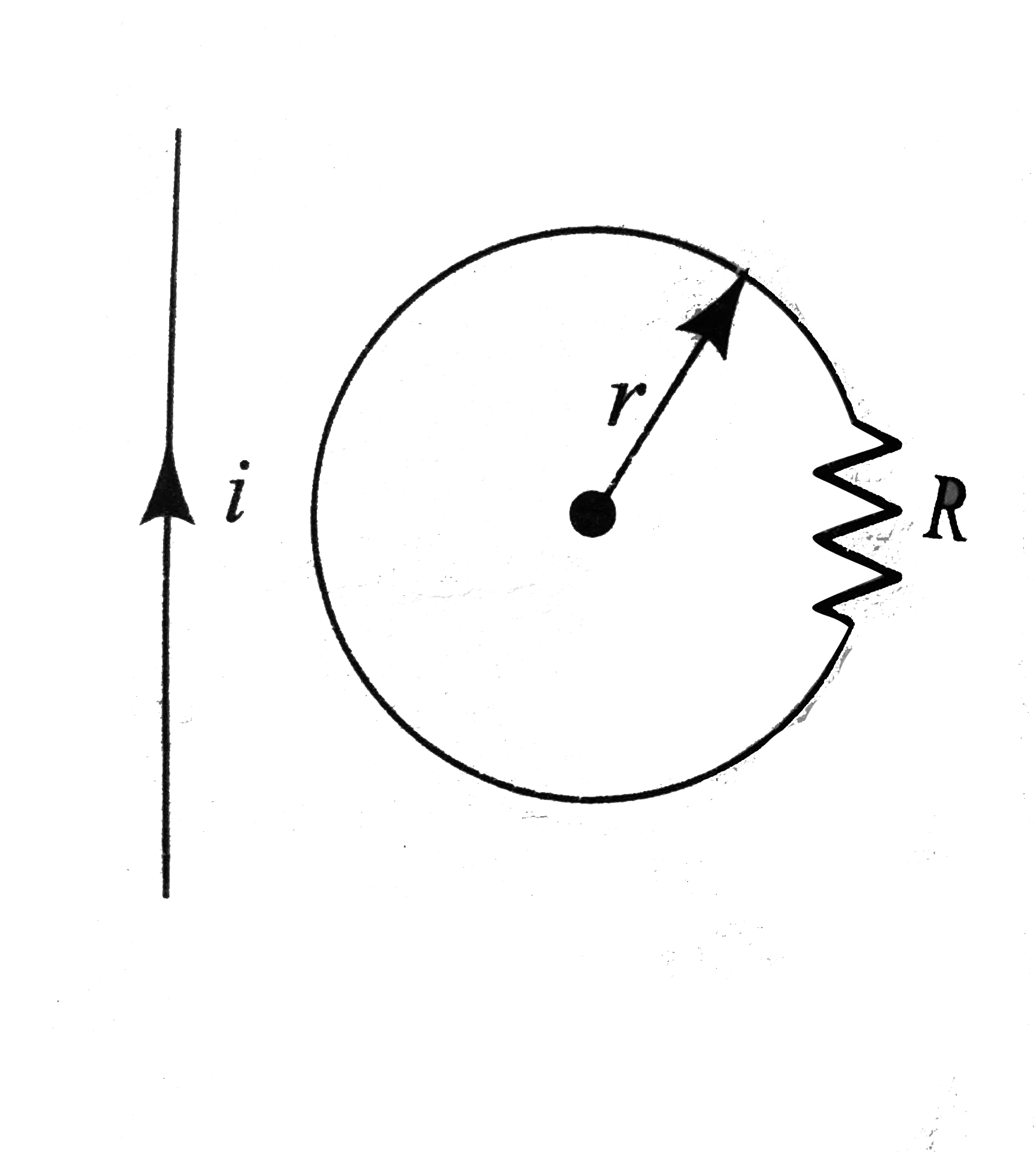 View Solution
View SolutionThe value of current I in the circuit will be
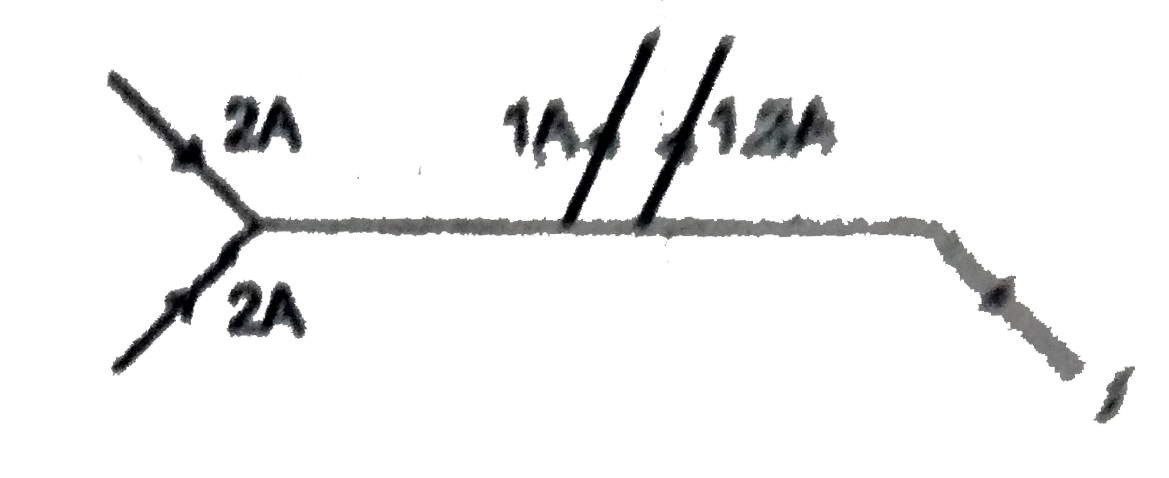 View Solution
View SolutionThe mean value of current for one complete cycle of shown current supply is
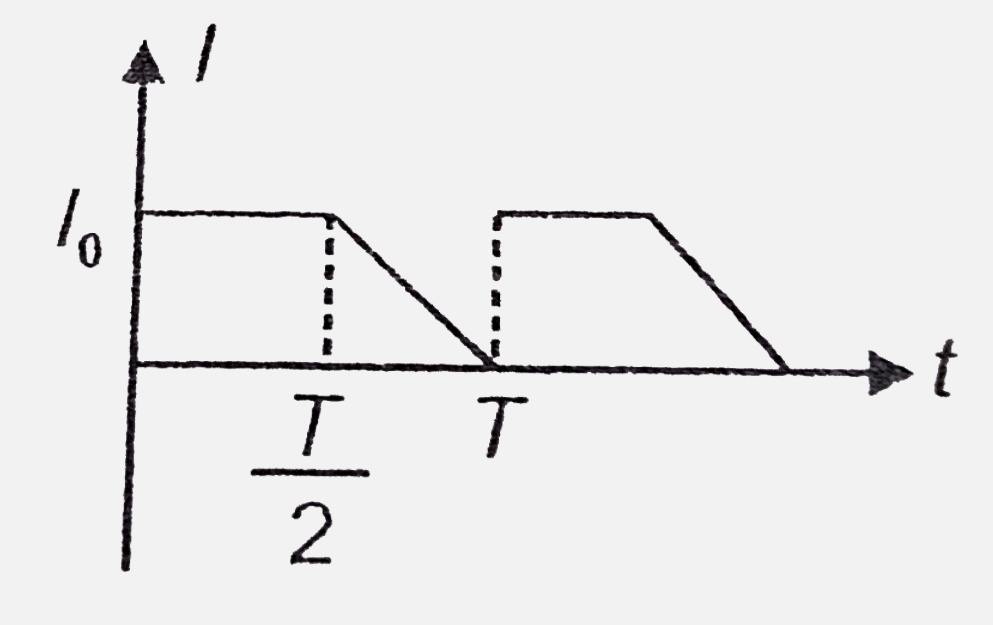 View Solution
View SolutionIf i=t2,0<t<T then r.m.s. value of current is
View SolutionThe current in a certain circuit varies with time as shown. The peak value of current is l0 . If ivandim represent the virtual (rms) and mean value of current for a complete cycle respectively, then
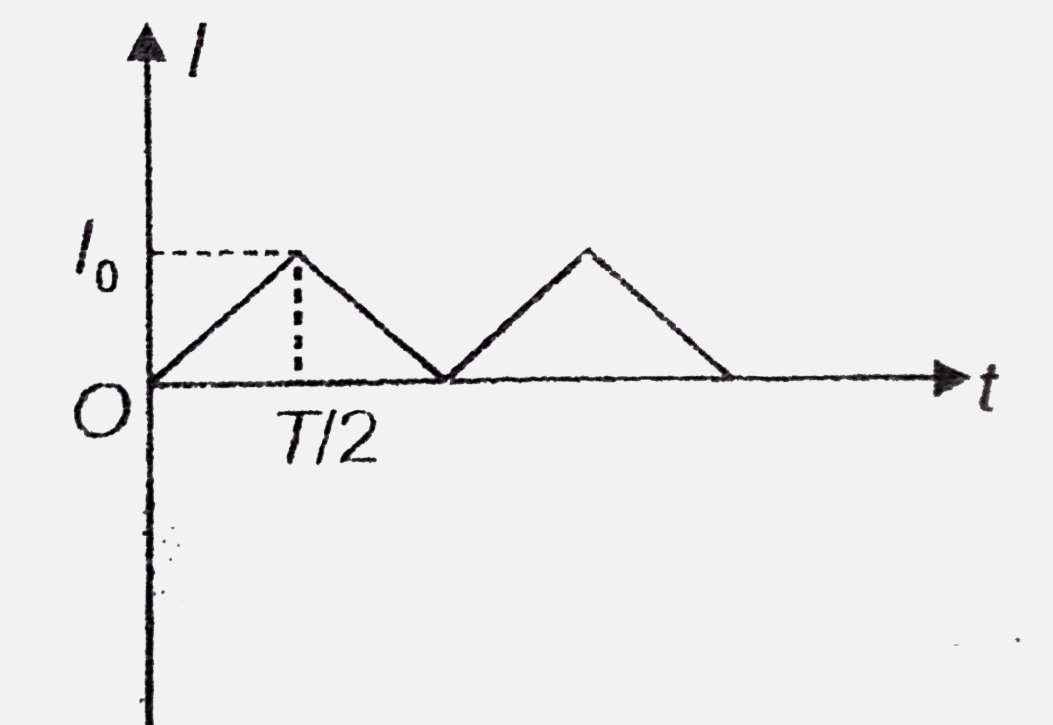 View Solution
View Solutionr.m.s. value of current i=3+4sin(ωt+π/3) is:
View Solutionr.m.s. value of current i=3+4sin (omegat+pi//3) is
View SolutionThe current in a discharging LR circuit is given by I=i0(tτ) where τ is the time constant of the circuit. Calculate the rms current for the period t=0 to t=τ.
View SolutionThe current in a discharging LR circuit is given by I=i0e−tτ where τ is the time constant of the circuit. Calculate the rms current for the period t=0 to t=τ.
View Solution
