Magnitude of magnetic field at a point P due to a current carrying wire, starting from origin and expanded to y-axis is
3μ0i20π
μ0i20π
3μ0i4π
3μ0i16π
To find the magnitude of the magnetic field at a point P due to a current-carrying wire that starts from the origin and extends along the y-axis, we can follow these steps:
1. Understanding the Setup:
- We have a current-carrying wire along the y-axis, and we need to calculate the magnetic field at point P with coordinates (3, 4).
- The distance from the wire to point P can be calculated using the coordinates.
2. Calculating the Distance (r):
- The distance r from the wire to point P can be found using the Pythagorean theorem.
- Here, r=√x2+y2=√32+42=√9+16=√25=5.
3. Identifying Angles:
- Let θ1 be the angle between the line connecting the wire to point P and the y-axis, and θ2 be the angle between the horizontal line (x-axis) and the line connecting the wire to point P.
- We can find θ1 using sinθ1=45 (opposite over hypotenuse).
4. Finding Sine Values:
- From the triangle formed, we have:
- sinθ1=45
- sinθ2=1 (since θ2=π2).
5. Using the Formula for Magnetic Field:
- The formula for the magnetic field B at a distance r from a long straight wire carrying current I is given by:
B=μ0I4πr(sinθ1+sinθ2)
- Substituting the values we have:
B=μ0I4π(5)(45+1)
6. Calculating the Magnetic Field:
- Simplifying further:
B=μ0I20π(45+1)=μ0I20π(45+55)=μ0I20π(95)
- Therefore:
B=9μ0I100π=3μ0I20π
7. Final Answer:
- The magnitude of the magnetic field at point P is:
B=3μ0I20π
- We have a current-carrying wire along the y-axis, and we need to calculate the magnetic field at point P with coordinates (3, 4).
- The distance from the wire to point P can be calculated using the coordinates.
- The distance r from the wire to point P can be found using the Pythagorean theorem.
- Here, r=√x2+y2=√32+42=√9+16=√25=5.
- Let θ1 be the angle between the line connecting the wire to point P and the y-axis, and θ2 be the angle between the horizontal line (x-axis) and the line connecting the wire to point P.
- We can find θ1 using sinθ1=45 (opposite over hypotenuse).
- From the triangle formed, we have:
- sinθ1=45
- sinθ2=1 (since θ2=π2).
- The formula for the magnetic field B at a distance r from a long straight wire carrying current I is given by:
B=μ0I4πr(sinθ1+sinθ2)
- Substituting the values we have:
B=μ0I4π(5)(45+1)
- Simplifying further:
B=μ0I20π(45+1)=μ0I20π(45+55)=μ0I20π(95)
- Therefore:
B=9μ0I100π=3μ0I20π
- The magnitude of the magnetic field at point P is:
B=3μ0I20π
Similar Questions
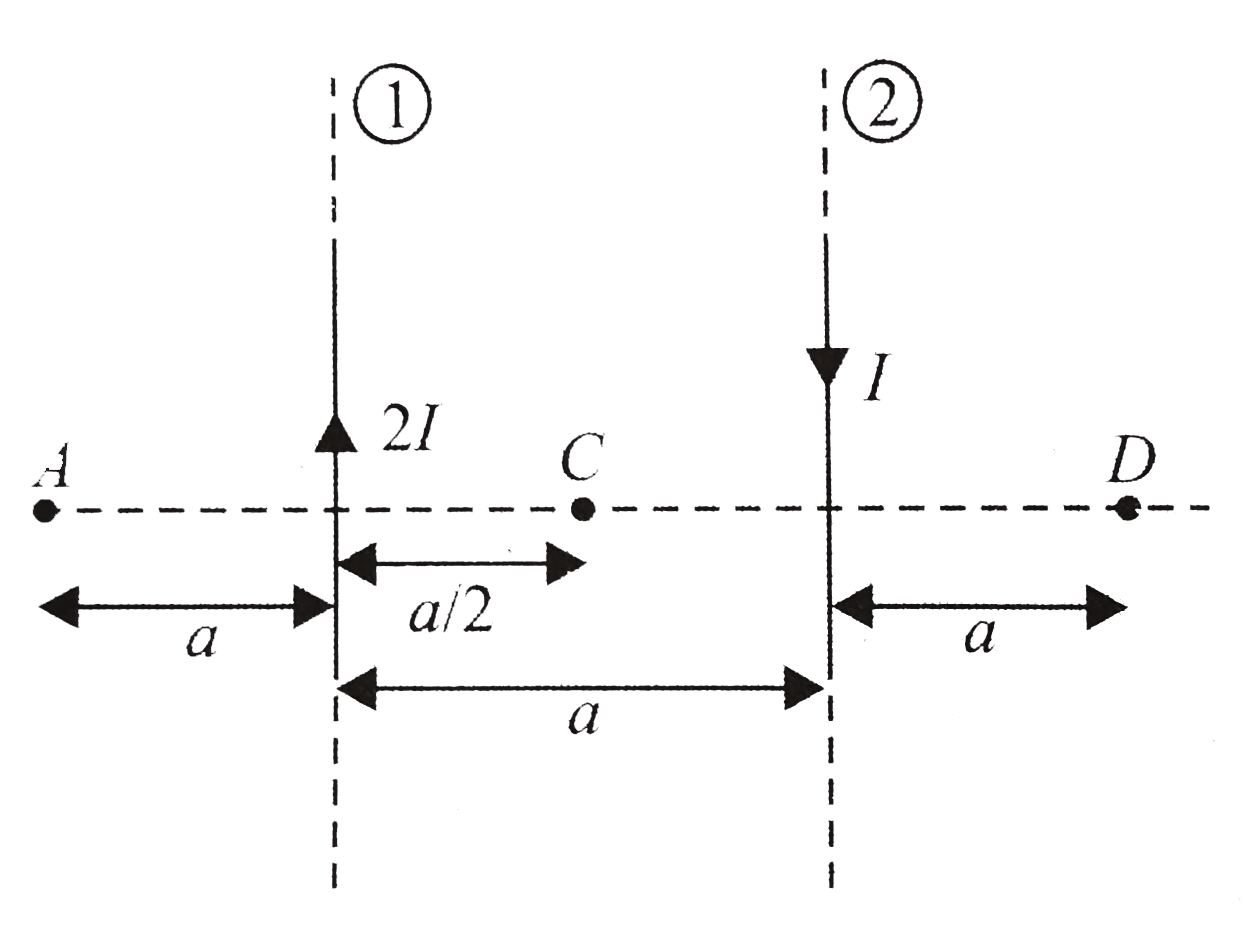
Find magnetic field at C by the system of current carrying wire.

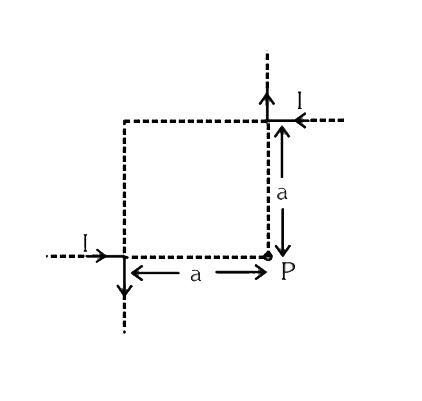
View SolutionMagnetic field at point 'P' due to given current distribution :-
View SolutionFind the magnitude and direction of magnetic field at point P due to the current carrying wire as shown in

View SolutionMagnetic field at a distance a from long current carrying wire is proportional to
View SolutionThe magnetic field at the origin due to the current flowing in the wire is

View SolutionThe magnetic field at the origin due to the current flowing in the wire is

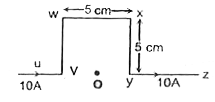
View SolutionThe resulting magnetic field at the point O due to the current carrying wire shown in the figure:
View SolutionThe magnetic field in a straight current carrying conductor wire is:
View SolutionConsider the magnetic field produced by a finitely long current carrying wire .
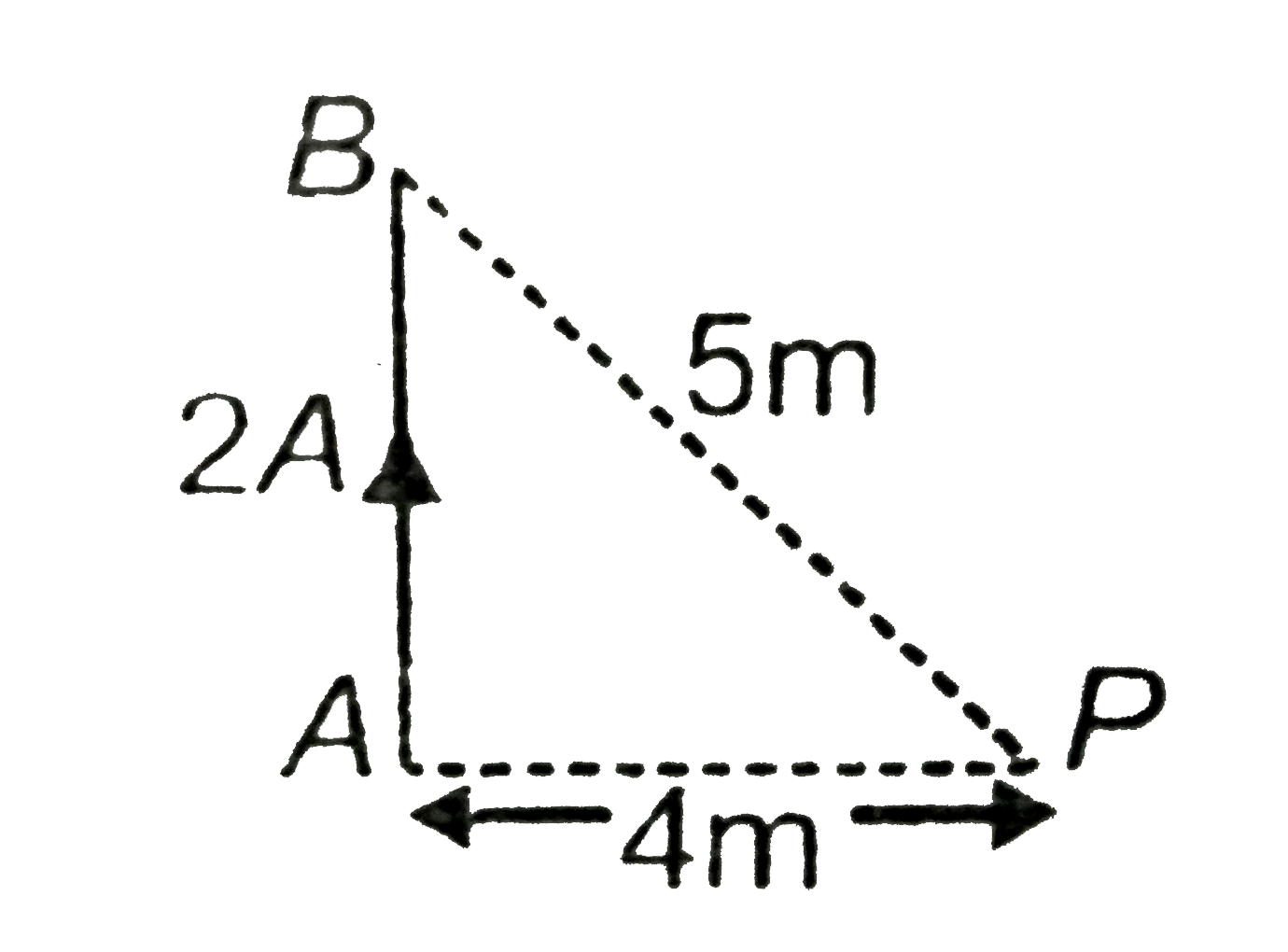
View SolutionWhat is the magnetic field ∣∣→B∣∣ at the point P due to a current carrying wire of length AB (having a current of 2A) shown in figure ?
View Solution
