Avarage value of current for half wave rectifier having peak value of current I0 is
A. I02
B. I0√2
C. I0π
D. 2I0π
The correct Answer is:C
To find the average value of current for a half-wave rectifier with a peak value of current I0, we can follow these steps:
1. Understand the Concept of Half-Wave Rectification:
- In a half-wave rectifier, only one half (positive or negative) of the AC waveform is allowed to pass through, while the other half is blocked. This results in a pulsating DC output.
2. Average Value Calculation:
- The average value of the output current over one complete cycle (which is 2π radians for a sine wave) can be calculated using the formula:
Iavg=1T∫T0I(t)dt
- For a half-wave rectifier, the current I(t) is I0sin(ωt) for 0≤t≤T2 and 0 for T2<t<T.
3. Setting Up the Integral:
- The average current over one cycle (T) can be expressed as:
Iavg=1T∫T/20I0sin(ωt)dt
- Since T=2πω, we can substitute T into the equation.
4. Evaluating the Integral:
- The integral can be evaluated as follows:
Iavg=1T⋅I0∫T/20sin(ωt)dt
- The integral of sin(ωt) is:
−1ωcos(ωt)∣∣∣T/20=−1ω(cos(π2)−cos(0))=−1ω(0−1)=1ω
5. Substituting Back:
- Now substituting back into the average current formula gives:
Iavg=1T⋅I0⋅1ω=I0T⋅ω
- Since T=2πω, we have:
Iavg=I0⋅ω2π⋅ω=I02π
6. Final Result:
- The average value of the current for a half-wave rectifier is:
Iavg=I0π
Conclusion:
Thus, the average value of current for a half-wave rectifier with a peak value of current I0 is I0π.
- In a half-wave rectifier, only one half (positive or negative) of the AC waveform is allowed to pass through, while the other half is blocked. This results in a pulsating DC output.
- The average value of the output current over one complete cycle (which is 2π radians for a sine wave) can be calculated using the formula:
Iavg=1T∫T0I(t)dt
- For a half-wave rectifier, the current I(t) is I0sin(ωt) for 0≤t≤T2 and 0 for T2<t<T.
- The average current over one cycle (T) can be expressed as:
Iavg=1T∫T/20I0sin(ωt)dt
- Since T=2πω, we can substitute T into the equation.
- The integral can be evaluated as follows:
Iavg=1T⋅I0∫T/20sin(ωt)dt
- The integral of sin(ωt) is:
−1ωcos(ωt)∣∣∣T/20=−1ω(cos(π2)−cos(0))=−1ω(0−1)=1ω
- Now substituting back into the average current formula gives:
Iavg=1T⋅I0⋅1ω=I0T⋅ω
- Since T=2πω, we have:
Iavg=I0⋅ω2π⋅ω=I02π
- The average value of the current for a half-wave rectifier is:
Iavg=I0π
Thus, the average value of current for a half-wave rectifier with a peak value of current I0 is I0π.
Similar Questions
If the peak value of a current in 50Hz AC. Cirucit is 7.07 A. What is the mean value of current over half a cycle and the value of current 1/300s after it was zero?
View SolutionThe instantaneous value of current at a given instant is 1 A and peak value of current is 53A .The potential difference between A and B at the same instant is
View Solution
Knowledge Check
The rms value of current in an ac circuit is 25 A, then peak current is
A35.36mAB35.36AC3.536AD49.38A
The value of form factor in case of half wave rectifier is
View SolutionIn a half wave rectifier, the current flows
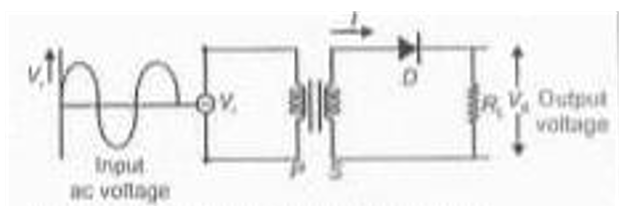
View SolutionThese question consists of two statements each linked as Assertion and Reason. While answering these question you are required to choose any one of the following five responses.
Assertion: Average value of current in half the cycle an AC circuit can't be zero.
Reason: For positive half cycle average value of current is 2π i0, where i0 is the peak value current. In time interval from t1 to t2 average value of current will be zero.
View SolutionIf reading of an ammeter is 10 A, the peak value of current is
View SolutionWhat is value of current I in given circuit
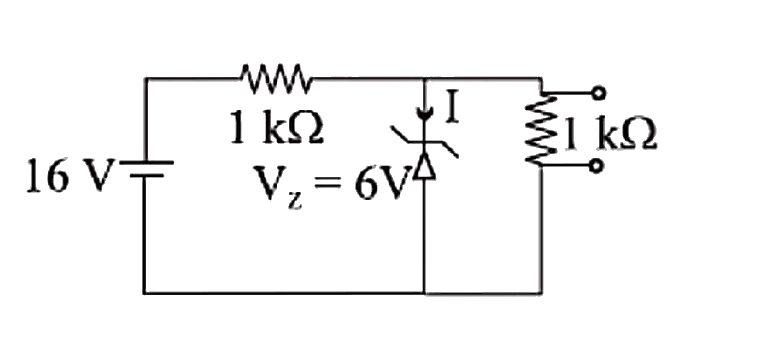
View SolutionThe value of current I in the circuit will be
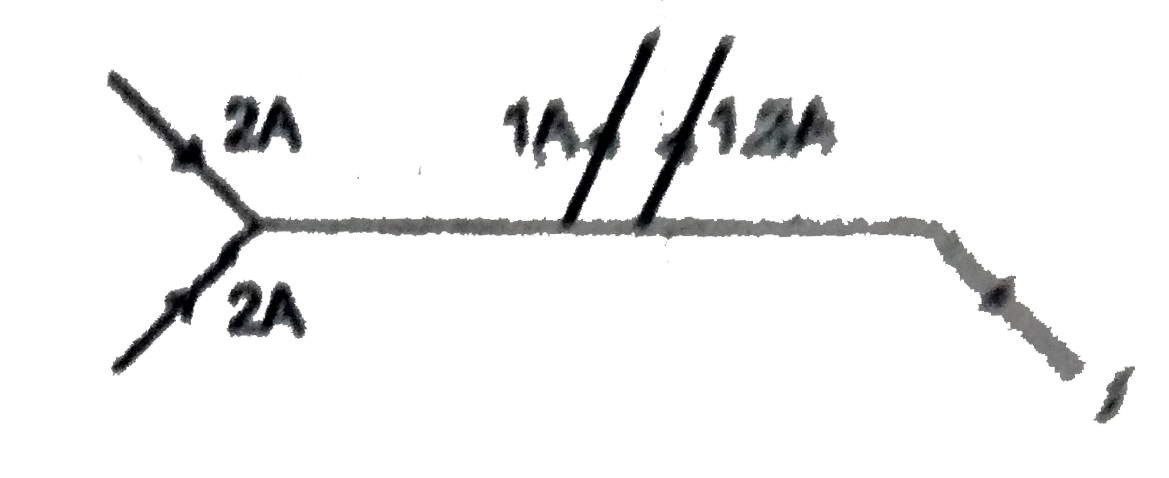
View SolutionThe value of current i1 in the given circuit is
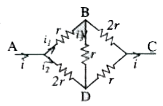
View Solution
