Magnetic in a region is given by →B=B0ˆi+B0ˆj . Torque on a circular loop x2+z2=r2 carrying current i in anticlockwise direction as seen from a point on positive y-axis is
iπr²B0ˆk
–iπr²B0ˆk
iπr²ˆk
–iπrB0ˆk
To solve the problem, we need to find the torque on a circular loop carrying a current in a magnetic field. Here’s a step-by-step solution:
Step 1: Understand the Magnetic Field and Loop
The magnetic field is given as:
→B=B0^i+B0^j
The circular loop is defined by the equation x2+z2=r2 and lies in the x-z plane, centered at the origin (0, 0, 0) with a radius r.
Step 2: Determine the Area Vector of the Loop
The area vector →A of the circular loop is directed along the positive y-axis since the current is flowing anticlockwise when viewed from the positive y-axis. The area A of the circle is:
A=πr2
Thus, the area vector is:
→A=πr2^j
Step 3: Calculate the Magnetic Moment
The magnetic moment →m of the loop is given by:
→m=i→A=i(πr2^j)=iπr2^j
Step 4: Calculate the Torque on the Loop
The torque →τ on the loop in a magnetic field is given by the cross product:
→τ=→m×→B
Substituting the values of →m and →B:
→τ=(iπr2^j)×(B0^i+B0^j)
This expands to:
→τ=(iπr2^j)×(B0^i)+(iπr2^j)×(B0^j)
Step 5: Evaluate the Cross Products
1. For the first term:
^j×^i=−^k(using the right-hand rule)
Thus,
(iπr2^j)×(B0^i)=iπr2B0(−^k)=−iπr2B0^k
2. For the second term:
^j×^j=0
Thus,
(iπr2^j)×(B0^j)=0
Step 6: Combine the Results
Combining the results from the cross products, we find:
→τ=−iπr2B0^k
Final Answer
The torque on the circular loop is:
→τ=−iπr2B0^k
The magnetic field is given as:
→B=B0^i+B0^j
The circular loop is defined by the equation x2+z2=r2 and lies in the x-z plane, centered at the origin (0, 0, 0) with a radius r.
The area vector →A of the circular loop is directed along the positive y-axis since the current is flowing anticlockwise when viewed from the positive y-axis. The area A of the circle is:
A=πr2
Thus, the area vector is:
→A=πr2^j
The magnetic moment →m of the loop is given by:
→m=i→A=i(πr2^j)=iπr2^j
The torque →τ on the loop in a magnetic field is given by the cross product:
→τ=→m×→B
Substituting the values of →m and →B:
→τ=(iπr2^j)×(B0^i+B0^j)
This expands to:
→τ=(iπr2^j)×(B0^i)+(iπr2^j)×(B0^j)
1. For the first term:
^j×^i=−^k(using the right-hand rule)
Thus,
(iπr2^j)×(B0^i)=iπr2B0(−^k)=−iπr2B0^k
^j×^j=0
Thus,
(iπr2^j)×(B0^j)=0
Combining the results from the cross products, we find:
→τ=−iπr2B0^k
The torque on the circular loop is:
→τ=−iπr2B0^k
Similar Questions
Find →a+→b if →a=ˆi−ˆj and →b=2ˆi
View SolutionA uniform magnetic field →B=3ˆi+4ˆj+ˆk exists in region of space. A semicircular wire of radius of 1 m carrying current 1 A having its centre at (2, 2, 0) is placed in x-y plane as shown in Fig. The force on semicircular wire will be
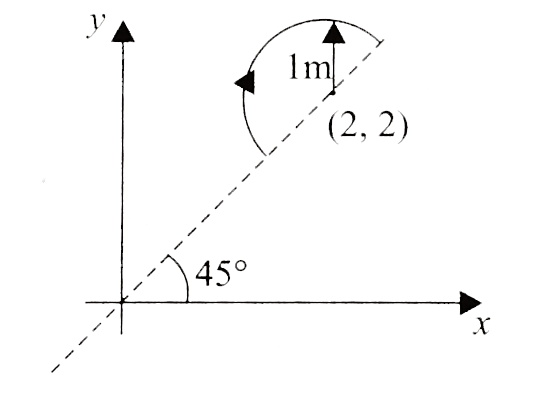
View SolutionA uniform magnetic field →B=3ˆi+4ˆj+ˆk exists in region of space. A semicircular wire of radius of 1 m carrying current 1 A having its centre at (2, 2, 0) is placed in x-y plane as shown in Fig. The force on semicircular wire will be
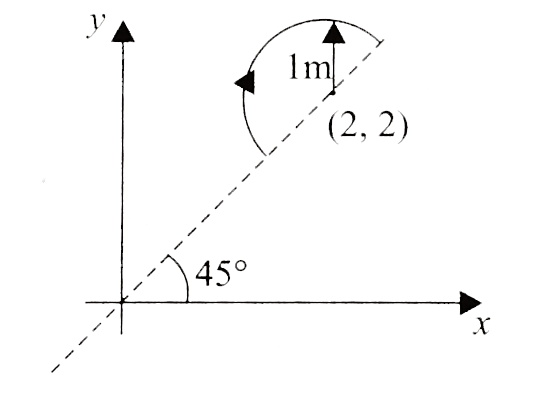
View SolutionThe magnetic field in a region is given by →B=B0(1+xa)ˆk. A square loop of edge length 'd' is placed with its edge along X-axis and Y-axis. The loop is moved with a constant velocity →V=V0ˆi. The emf induced in the loop is
View SolutionFor given vector, →a = 2ˆi j +2ˆk and →b = -ˆi +ˆj - ˆk , find the unit vector in the direction of the vector →a +→b .
View SolutionWrite a unit vector in the direction of →b=2ˆi+ˆj+2ˆk.
View SolutionIf →a=ˆi+ˆj,→b=ˆj+ˆk,→c=ˆk+ˆi find the unit vector in the direction of →a+→b+→⋅
View SolutionFind ∣∣→a×→b∣∣ , if →a=ˆi−7ˆj+7ˆkand→b=3ˆi−2ˆj+2ˆk.
View SolutionFind ∣∣→a×→b∣∣, if →a=ˆi−7ˆj+7ˆkand →b=3ˆi−2ˆj+2ˆk
View SolutionFind ∣∣→a×→b∣∣,if →a=2ˆi+ˆj+3ˆkand →b=3ˆi+5ˆj−2ˆk.
View Solution
