The velocities of our molecules are $V$ , $2 V$ , $4 V$ and $\sqrt 2 V$ , respectively. Their r.m.s. speed is

$2.4$ v

$2.2$ v

$24$ v

$0.2$ v

Video Solution

Answer

Step by step video & image solution for The velocities of our molecules are V, 2V, 4V and √2V, respectively. Their r.m.s. speed is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS MOCK TEST 6

Similar Questions

The velocities of three molecules are 3v, 4v and 5v. Calculate their root mean square velocity.
View Solution
The velocities of three molecules are 3v, 4v and 5v. Calculate their root mean square velocity.
View Solution
If the velocities of three gas molecules are $\sqrt{7}$ , 4 and 5 m/s, then there $V_{r m s}$ ( in m/s) will be
View Solution
If speeds of the four molecules of an ideal gas are v, 3v, 5v and 7v respectively, then the mean square speed of the molecules will be
View Solution
A proton a deutron and an $α$ particle are accelerated through potentials of $V, 2 V$ and $4 V$ respectively. Their velocity will bear a ratio
View Solution
A proton a deutron and an $α$ particle are accelerated through potentials of $V, 2 V$ and $4 V$ respectively. Their velocity will bear a ratio
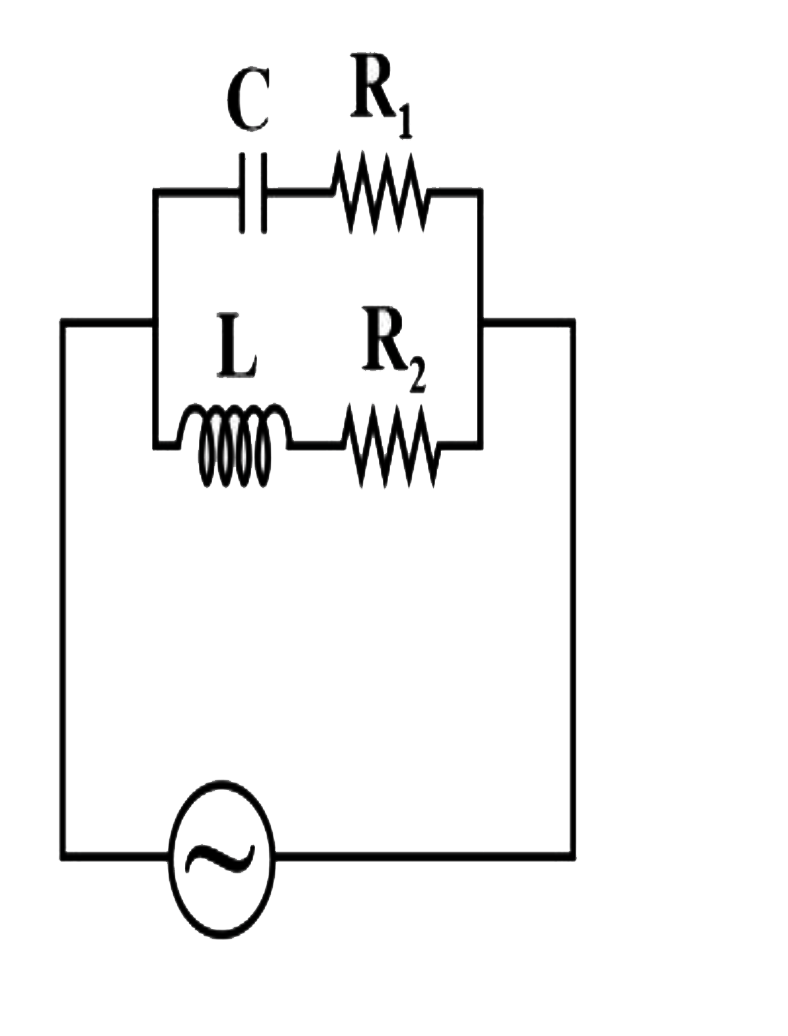
View Solution
In the given circuit the R.M.S values of voltages across the capacitor C, inductor L and resistor $R_{1}$ are 12V, 10V and 5 V respectively. Then the peak voltage across $R_{2}$ is

View Solution
A uniform electric fied exists in x-y plane. The potential of ponts $A (2 m, 2 m), B (- 2 m, 2 m)$ and $C (2 m, 3 m)$ are $4 V, 16 V$ and $12 V$ respectively. The electric field is
View Solution
Two identical photo-cathodes receive light of frequencies $v_{1}$ and $v_{2}$ . If the velocities of the photoelectrons (of mass m) coming out are $v_{1}$ and $v_{2}$ respectively, then
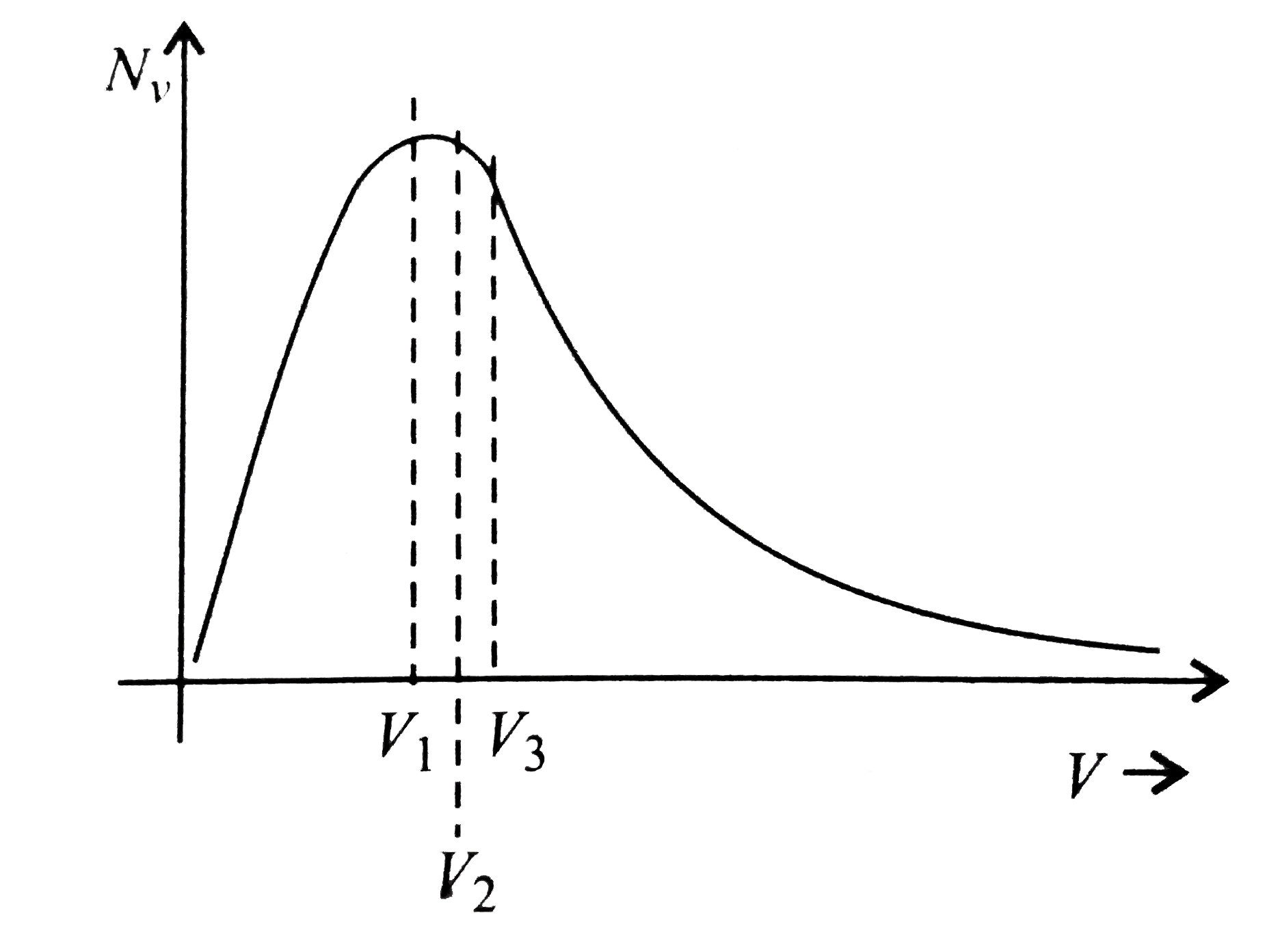
View Solution
The distribution of the molecular velocities of gas molecules at any temperature $T$ is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)

where
$v$ is molecular velocity
$n$ is number of molecules having velocity $v$
Let us define $Δ N_{v}$ , which is equal to the number of molecules between the velocity range $v$ and $v + Δ v$ , given by
$Δ N_{v} = 4 π N a^{3} e^{- b v^{2}} v^{2} Δ v$
where
$N$ is total number of molecules
$a = \sqrt{\frac{M_{0}}{2 π R T}}$ and $b = \frac{M_{0}}{2 R T}$
$R$ is universal gas constant
$T$ is temperature of the gas
$M_{0}$ is molecular weight of the gas
Answer the following question:
$S I$ units of $a$ are
View Solution

The velocities of our molecules are V, 2V, 4V and √2V, respectively. Their r.m.s. speed is

Similar Questions

Recommended Questions

The velocities of our molecules are $V$ , $2 V$ , $4 V$ and $\sqrt 2 V$ , respectively. Their r.m.s. speed is