The position of S.H.M. is given by x=2[√3sin πt +cos πt]. The amplitude of motion is [ x is in metre and symbols have the usual meaning]
2m
4m
1m
√3 m
To find the amplitude of the simple harmonic motion (S.H.M.) described by the equation x=2(√3sin(πt)+cos(πt)), we can follow these steps:
Step 1: Identify the coefficients
The equation can be rewritten as:
x=2√3sin(πt)+2cos(πt)
Here, the coefficient of sin(πt) is 2√3 and the coefficient of cos(πt) is 2.
Step 2: Use the amplitude formula
The amplitude A of the S.H.M. can be calculated using the formula:
A=√(a2+b2)
where a is the coefficient of sin and b is the coefficient of cos.
Step 3: Substitute the coefficients
Substituting the coefficients into the formula:
A=√(2√3)2+(2)2
Calculating each term:
(2√3)2=4×3=12
(2)2=4
Step 4: Add the squares
Now, add the two results:
A=√12+4=√16
Step 5: Take the square root
Taking the square root gives:
A=4
Conclusion
Thus, the amplitude of the motion is 4 meters.
---
The equation can be rewritten as:
x=2√3sin(πt)+2cos(πt)
Here, the coefficient of sin(πt) is 2√3 and the coefficient of cos(πt) is 2.
The amplitude A of the S.H.M. can be calculated using the formula:
A=√(a2+b2)
where a is the coefficient of sin and b is the coefficient of cos.
Substituting the coefficients into the formula:
A=√(2√3)2+(2)2
Calculating each term:
(2√3)2=4×3=12
(2)2=4
Now, add the two results:
A=√12+4=√16
Taking the square root gives:
A=4
Thus, the amplitude of the motion is 4 meters.
Similar Questions
An SHM is give by y=5[sin(3πt)+√3cos(3πt)]. What is the amplitude of the motion of y in metre ?
View SolutionAccording to Newton's 2nd law of motion correct equation is (where symbols have their usual meanings)
View SolutionIf H=1√3V, then find angle of dip. (where symbols have their usual meaning)
View SolutionConsider the situation in which one end of a massless spring of spring constant k is connected to a cylinder of mass m and the other to a rigid support. When cylinder is given a gentle push in horizontal direction it starts oscillating on the rough horizontal surface. During the oscillation cylinder rolls without slipping. When calculated, motion of cylinder is found to be S.H.M. with time period T=2π√3m2K and equation of SHM is x=Asinωt, where symbols have their usual meaning.
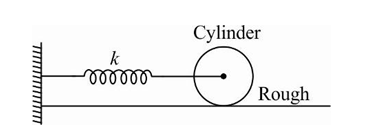
At a distance x1 from the equilibrium position, kinetic energy of the oscillating system becomes equal to potential energy then, x1is equal to:View SolutionThe displacement of a particle is given by x=3sin(5πt)+4cos(5πt). The amplitude of particle is
View SolutionThe equation of a travelling wave is given as y=Asin2π(αt−βx).Theratioofmaxiμmpartic≤speed→wavespeedis(wheresymbolshavetheirusualmean∈gandalpha, beta are constants)
View SolutionThe SHM of a particle is given by the equation x=2sinωt+4cosωt. Its amplitude of oscillation is
View SolutionIf in a △ABC , cos (A-C) cos B + cos 2 B =0 , then which of the following options is(are) correct? (where, the symbols have their usual meanings).
View SolutionAssertion : In x=3+4 cosωt , amplitude of oscillation is 4 units.
Reason : Mean position is at x=3.View SolutionThe simple harmonic motion of a particle is given by x = a sin 2πt . Then, the location of the particle from its mean position at a time 1/8th of second is
View Solution

