A square loop of sides L is placed at centre of a circular loop of radius r (r << L) such that they are coplanar, then mutual inductance between both loop is
μ0L4r
μ0L2r
μ0L24r
μ0L22r
To find the mutual inductance between a square loop of side L and a circular loop of radius r (where r≪L), we can follow these steps:
1. Understanding the Configuration:
- We have a square loop with side length L placed at the center of a circular loop with radius r. Since r is much smaller than L (i.e., r≪L), we can consider the magnetic field produced by the circular loop to be uniform across the area of the square loop.
2. Magnetic Field Due to the Circular Loop:
- The magnetic field B at the center of a circular loop carrying a current I is given by the formula:
B=μ0I2r
- Here, μ0 is the permeability of free space.
3. Area of the Square Loop:
- The area A of the square loop is:
A=L2
4. Magnetic Flux Through the Square Loop:
- The magnetic flux Φ through the square loop due to the magnetic field B is given by:
Φ=B⋅A=(μ0I2r)⋅L2
5. Induced EMF and Mutual Inductance:
- The mutual inductance M is defined as the ratio of the magnetic flux Φ through one loop to the current I in the other loop:
M=ΦI
- Substituting the expression for Φ:
M=(μ0I2r)⋅L2I
6. Simplifying the Expression:
- The current I cancels out:
M=μ0L22r
7. Final Result:
- Therefore, the mutual inductance M between the square loop and the circular loop is:
M=μ0L22r
Conclusion:
The mutual inductance between the square loop and the circular loop is given by:
M=μ0L22r
- We have a square loop with side length L placed at the center of a circular loop with radius r. Since r is much smaller than L (i.e., r≪L), we can consider the magnetic field produced by the circular loop to be uniform across the area of the square loop.
- The magnetic field B at the center of a circular loop carrying a current I is given by the formula:
B=μ0I2r
- Here, μ0 is the permeability of free space.
- The area A of the square loop is:
A=L2
- The magnetic flux Φ through the square loop due to the magnetic field B is given by:
Φ=B⋅A=(μ0I2r)⋅L2
- The mutual inductance M is defined as the ratio of the magnetic flux Φ through one loop to the current I in the other loop:
M=ΦI
- Substituting the expression for Φ:
M=(μ0I2r)⋅L2I
- The current I cancels out:
M=μ0L22r
- Therefore, the mutual inductance M between the square loop and the circular loop is:
M=μ0L22r
The mutual inductance between the square loop and the circular loop is given by:
M=μ0L22r
Similar Questions
A small square loop of n1 turns and side l is placed at the centre of a large coplanar, circular loop of radius r and n2 tuns. The mutual inductacne of the combination is
View SolutionA circular loop of radius r carrying a current i is held at the centre of another circular loop of radius R(>> r) carrying a current I. The plane of the smaller loop makes an angle of 30∘ with that of the larger loop. It the smaller loop is held fixed in this position by applying a single force at a point on its periphery, what would be the minimum magnitude of this force?
View Solution
Knowledge Check
A small square loop of wire of side l is placed inside a large square loop of wire of side L(L>>l). The loops are coplanar and their centre coincide. What is the mutual inductance of the system ?
A2√2μ0πl2LB8√2μ0πl2LC2√2μ02πl2LD2√2μ0L2πl
Find mutual inductance if we have a square loop of side r instead of a small circular loop of side r at the centre of bigger circular loop.
View SolutionA small square loop of wire of side l is placed inside a large square loop of wire of side L(L>>l). The loops are co-planer and their centres coincide. The mutual inductance of the system is proportional to
View SolutionA square loop of side a is placed in the same plane as a long straight wire carrying a current i. The centre of the loop is at a distance r from wire where r>>a. The loop is moved away from the wire with a constant velocity v. The induced e.m.f in the loop is
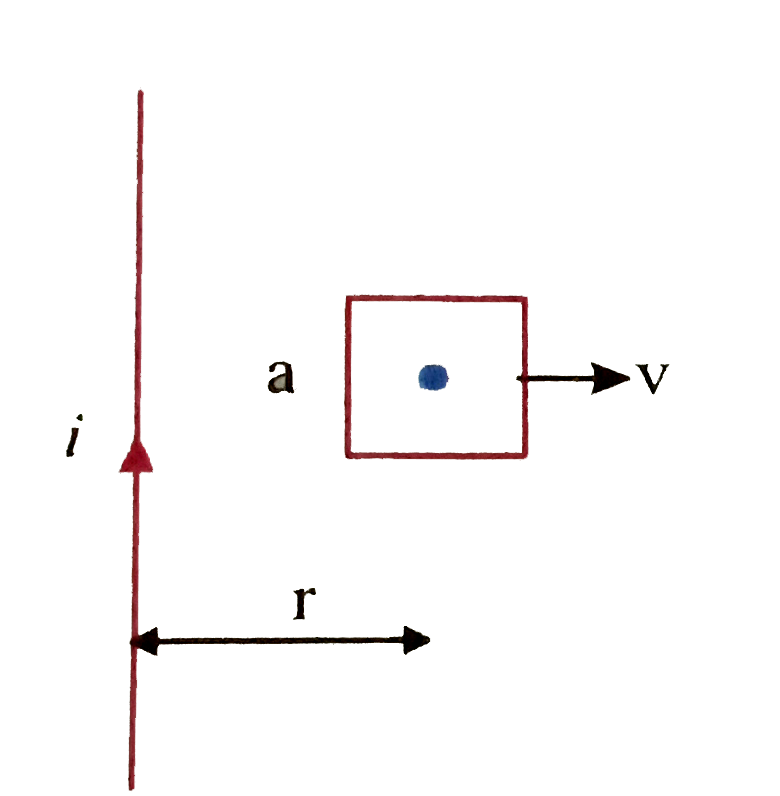
View SolutionA circular loop of radius R carries a current I. Another circular loop of radius r(ltltR) carries a current I. The plane of the smaller loop makes an angle of 90^@ with that of the larger loop. The planes of the two circles are at right angle to each other. Find the torque acting on the smaller loop.
View SolutionA small circular loop of wire of radius a is located at the centre of a much larger circular wire loop of radius b. The two loops are in the same plane. The outer loop of radius b carries an alternating current I=I0cos(ωt). The emf induced in the smaller inner loop is nearly ?
View SolutionA circular loop of radius 0.3 cm lies parallel to amuch bigger circular loop of radius 20 cm. The centre of the small loop is on the axis of the bigger loop. The distance between their centres is 15 cm. If a current of 2.0 A flows through the smaller loop, then the flux linked with bigger loop is
View SolutionA circular loop of radius 0.3 cm lies parallel to amuch bigger circular loop of radius 20 cm. The centre of the small loop is on the axis of the bigger loop. The distance between their centres is 15 cm. If a current of 2.0 A flows through the smaller loop, then the flux linked with bigger loop is
View Solution
